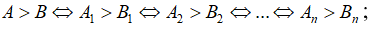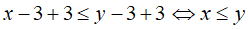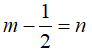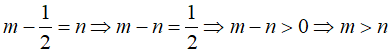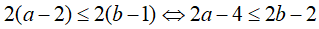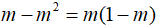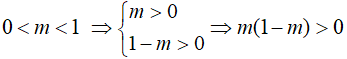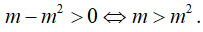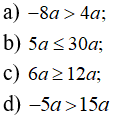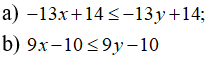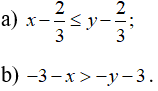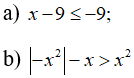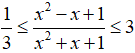Cách so sánh hai biểu thức, hai số hay, chi tiết
Cách so sánh hai biểu thức, hai số hay, chi tiết
Tài liệu Cách so sánh hai biểu thức, hai số hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
Dạng bài : So sánh hai số, hai biểu thức
A. Phương pháp giải
*Các phương pháp chứng minh A>B; (A<B tương tự):
1) Dùng định nghĩa chứng minh A-B>0 (Xét hiệu hai vế).
2) Biến đổi tương đương:
Nếu An>Bn đúng thì A>B đúng.
3) Phản chứng: Giả sử A≤B dẫn tới một điều vô lý. Vậy A>B.
4) Chứng minh bằng quy nạp toán học:
+ Bước 1: Chứng minh bất đẳng thức đúng với n=n0.
+ Bước 2: Giả sử bất đẳng thức đúng với n=k (k≥n0), ta chứng minh bất đẳng thức đúng với n=k+1.
Từ đó kết luận bất đẳng thức đúng với mọi số tự nhiên n≥n0.
(Phương pháp quy nạp toán học thường được sử dụng khi trong bất đẳng thức có sự tham gia của n với vai trò của một số nguyên dương tùy ý hoặc số nguyên dương lấy mọi giá trị bắt đầu từ n0 nào đó).
5) Phương pháp tổng hợp:
+ Sử dụng tính chất và các hằng bất đẳng thức.
+ Sử dụng tính chất bắc cầu (làm trội) A>C; C>B ⇒A>B.
B. Ví dụ minh họa
Câu 1: Cho x-3 ≤ y-3, so sánh x và y
Lời giải:
Cộng hai vế của bất đẳng thức với 3 ta được:
Câu 2: So sánh m và n biết
Lời giải:
Ta có
Câu 3: Cho a-2 ≤ b-1. So sánh hai biểu thức 2a-4 và 2b-2
Lời giải:
Nhân cả 2 vế của bất đẳng thức với 2 ta được:
Câu 4: So sánh m và m2 với 0<m<1.
Lời giải:
Xét hiệu:
Ta có vì
hay
C. Bài tập tự luyện
Câu 1: Cho a> b, hãy so sánh:
a) 3a+5 và 3b+2. b) 2-4a<3-4b.
Câu 2: Cho m > n, chứng minh:
a) 2019 - n > 2018-m; b) -1 - m < -n + 2.
Câu 3: Số a là âm hay dương nếu:
Câu 4: So sánh x và y nếu:
Câu 5: Cho x + 5 > 15. Chứng minh x - 2 > 8.
Câu 6: So sánh x và y trong mỗi trường hợp sau:
Câu 7: So sánh x và 0 trong mỗi trường hợp sau:
Câu 8: Cho a > b. Chứng minh a + 1 + 2 + 3 +...+ 9 + 10 > b + 54.
Câu 9: Chứng minh
với mọi giá trị của x.
