Cách chia đa thức một biến đã sắp xếp cực hay, có lời giải chi tiết
Cách chia đa thức một biến đã sắp xếp cực hay, có lời giải chi tiết
Tài liệu Cách chia đa thức một biến đã sắp xếp cực hay, có lời giải chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
Định nghĩa: Với A là đa thức và B là đơn thức, B ≠ 0. Ta nói A chia hết cho B nếu tìm được một biểu thức Q (Q có thể là đa thức hoặc đơn thức) sao cho A = B.Q.
Trong đó:
. A là đa thức bị chia.
. B là đơn thức chia.
. Q là thương .
Kí hiệu: Q = A : B hoặc 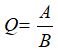
Quy tắc: Muốn chia đa thức A cho đơn thức B (trường hợp các hạng tử của đa thức A đều chia hết cho đơn thức B), ta chia mỗi hạng tử của A cho B rồi cộng các kết quả với nhau.
Chú ý: Trường hợp đa thức A có thể phân tích thành nhân tử, thường ta phân tích trước để rút gọn cho nhanh.
B. Ví dụ minh họa
Ví dụ 1: Thực hiện phép tính (12x4y3 + 8x3y2 - 4xy2) : 2xy
A. 6x3y2 + 4x2y - 2y
B. 6x2y2 + 4x2y - 2xy
C. 6x2y2 + 4x2y - 2xy2
D. Đáp án khác
Lời giải
(12x4y3 + 8x3y2 - 4xy2):2x = (12x4y3 : 2xy) + (8x3y2 : 2xy) - (4xy2 : 2xy)
= 6x4-1.y3-1 + 4x3-1.y2-1 - 2x1-1.y2-1 = 6x3y2 + 4x2y - 2y
Chọn A.
Ví dụ 2. Thực hiện phép tính (-2x5 + 6x2 - 4x3):2x2
A. – x3 + 2x – 3 B. x3- 2x- 3 C. - x3 – 2x + 3 D. - x2 + 2x - 3
Lời giải
(-2x5 + 6x2 - 4x30) : 2x2 = (-2x5 : 2x2) + (6x2 : 2x2) - (4x3 : 2x2)
= -x5-2 + 3x2-2 - 2x3-2 = -x3 + 3 - 2x
Chọn C.
Ví dụ 3. Thực hiện phép tính (-8x5 + 12x3 - 16x2) : 4x2
A. – 2x3 + 3x – 4 B. 2x2 + 3x + 4x C. 2x3 + 3x + 4 D. Đáp án khác
Lời giải
(-8x5 + 12x3 - 16x2) : 4x2
= (-8x5 : 4x2) + (12x3 : 4x2) + (-16x2 : 4x2)
= -2x3 + 3x - 4
Chọn A.
Ví dụ 4. Thực hiện phép tính 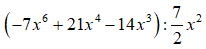
A. -2x4 + 6x2 - 4x B. -2x4 - 6x2 - 4 C. 2x4 - 6x2 - 4x D. Đáp án khác
Lời giải
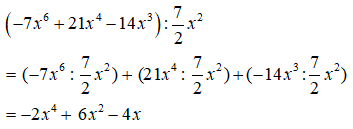
Chọn A.
C. Bài tập trắc nghiệm
Câu 1. Thực hiện phép tính (-2x5 + 3x2 - 4x3) : 2x2

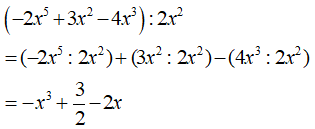
Chọn B.
Câu 2. Thực hiện phép tính 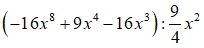

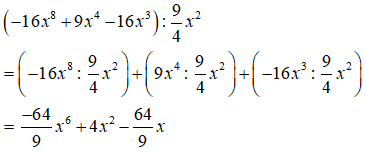
Chọn C.
Câu 3. Thực hiện phép tính 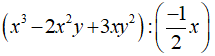
A. -2x2 - 4xy - 6y B. -2x2 + 4y + 3y2 C. 2x2 + 4y - 6y2 D. -2x2 + 4xy - 6y2
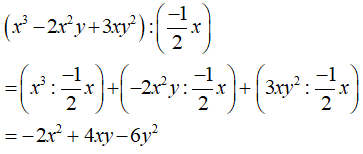
Chọn D.
Câu 4. Thực hiện phép tính (12x3y3 - 18x2y + 9xy2):6xy
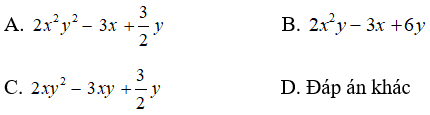
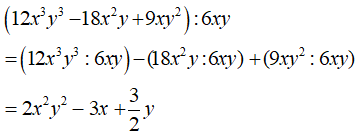
Chọn A.
Câu 5. Thực hiện phép tính (-8x7y3 + 12x4y - 4x3y) : 8x3y

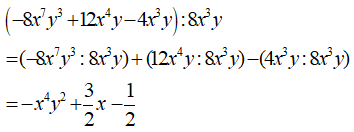
Chọn C
Câu 6. Thực hiện phép tính (15x3y3 - 10x2y3 + 25x2y2):5x2y2
A. 3xy + 2y + 5
B. 3xy – 2y + 5
C. 3xy + 2x + 5
D. 3xy – 2x + 5
(15x3y3 - 10x2y3 + 25x2y2):5x2y2
= (15x3y3 : 5x2y2) - (10x2y3 : 5x2y2) + (25x2y2 : 5x2y2)
= 3xy - 2y + 5
Chọn B.
Câu 7. Thực hiện phép chia: (2x4y - 6x2y7 + 4x5) : 2x2
A. x2y - 3y7 + 2x3
B. x2y - 3xy7 + 2x3
C. 4x2y - 6y7 + 4x3
D. Đáp án khác
(2x4y - 6x2y7 + 4x5):2x2
= 2x4y : 2x2 - 6x2y7 : 2x2 + 4x5 : 2x2
= x2y - 3y7 + 2x3
Chọn A.
Câu 8. Tính giá trị biểu thức A = (4x2y3z + 2x3y2z2 - x2y2) : x2y2 tại x = -2; y = 102; z= 102
A. 1029 B. -1028 C. 30 D. -1
A = (4x2y3z + 2x3y2z2 - x2y2) : x2y2
= 4x2y3z : x2y2 + 2x3y2z2 : x2y2 - x2y2 : x2y2
= 4yz + 2xz2 - 1
Giá trị biểu thức tại x = -2; y = 102; z= 102 là:
A = 4.1020.102 + 2.(-2).1022 - 1
= 4.1022 - 4.1022 - 1 = -1
Chọn D.
Câu 9. Làm tính chia: (2x2z5 - y3z3 + 4z6) : z3
A. 2x2z2 – y3 + 4z3
B. 2x2z2 – y3z + 4z3
C. 2x2z2 – y3 + 4z3 + 1
D.Đáp án khác
(2x2z5 - y3z3 + 4z6) : z3
= 2x2z5 : z3 - y3z3 : z3 + 4z6 : z3
= 2x2z2 – y3 + 4z3
Chọn A.
Câu 10. Tìm đa thức A biết :
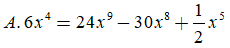

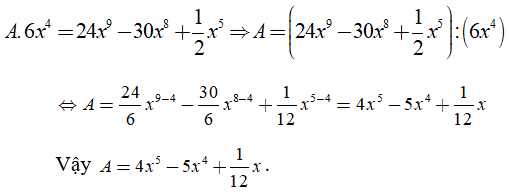
Chọn A.
Câu 11. Tìm đa thức A biết: 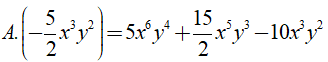
A. A = -2x3y - 3x2y + 4
B. A = -2x3y2 - 3x2y + 4
C. A = -2x2y2 - 3xy + 4
D. Đáp án khác
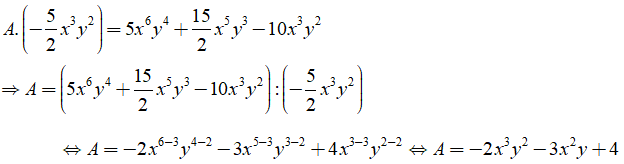
Vậy A = -2x3y2 - 3x2y + 4.
Chọn B

