Chứng minh hai đoạn thẳng, hai góc bằng nhau hay, chi tiết

Chứng minh hai đoạn thẳng, hai góc bằng nhau hay, chi tiết

Tài liệu Chứng minh hai đoạn thẳng, hai góc bằng nhau hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải.

Sử dụng:

• Tính chất về cạnh bên và đường chéo của hình thang cân: Trong hình thang cân, hai cạnh bên bằng nhau, hai đường chéo bằng nhau.
• Hình thang có hai đường chéo bằng nhau là hình thang cân.
• Trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau.
• Áp dụng định lý Py - ta - go.

B. Ví dụ minh họa

Ví dụ 1. Hình thang ABCD (AB//CD, AB < CD). Kẻ các đường cao AH, BK của hình thang. Chứng minh rằng DH = CK.

Giải

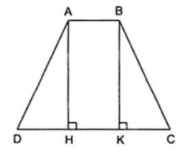
Áp dụng định nghĩa, tính chất và giả thiết vào hình thang cân ABCD, ta được:

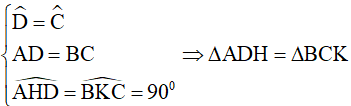
(trường hợp cạnh huyền - góc nhọn).

Vậy DH = CK.

Ví dụ 2. Cho hình thang cân ABCD (AB//CD) có I là giao điểm của hai đường chéo. Chứng minh rằng: IC = ID và IA = IB.

Giải

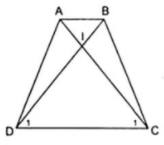
Áp dụng tính chất về cạnh bên và đường chéo vào hình thang cân ABCD, ta được:

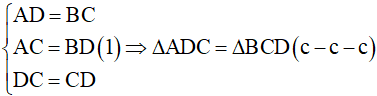
Suy ra 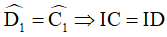(2) (vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau).

Trừ theo vế các đẳng thức (1) và (2) ta được: AC – IC = BD – ID ⇒ IA = IB.

Ví dụ 3. Cho hình thang ABCD (AB//CD) hai đường phân giác của góc C và D cắt nhau tại điểm I thuộc đáy AB. Chứng minh rằng tổng hai cạnh bên bằng đáy AB của hình thang.

Giải

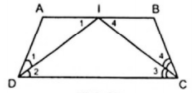
Áp dụng tính chất góc so le của AB//CD và giả thiết, ta có:

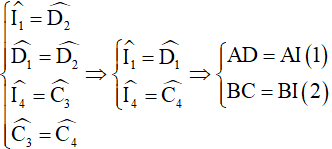
(vì trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau).

Cộng theo vế các đẳng thức (1) và (2) ta được AD + BC = AI + BI = AB.

Điều này chứng tỏ tổng hai cạnh bên bằng đáy AB của hình thang.

Ví dụ 4. Cho tam giác ABC cân tại A, các đường phân giác BD, CE . Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Giải

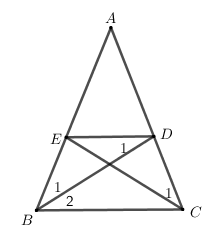
Xét ΔABD và ΔACE có:

AB = AC (tam giác ABC cân tại A)

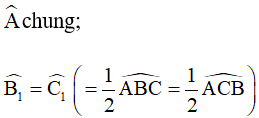
Nên ΔABD=ΔACE (g-c-g). Suy ra AD = AE

Suy ra tam giác ADE cân tại A

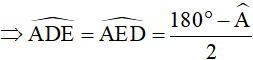
Mà

(tam giác ABC cân tại A)

Do đó: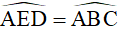 , mà hai góc này ở vị trí đồng vị nên ED // BC

Suy ra tứ giác BEDC là hình thang có hai góc ở đáy 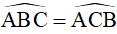(ΔABC cân tại A)

Nên BEDC là hình thang cân.

Lại có: ED // BC nên suy ra 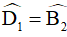(so le trong)

Lại có 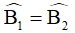(tính chất tia phân giác) nên .

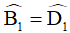Do đó tam giác EBD cân tại E. Suy ra EB = ED.

Vậy BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Ví dụ 5. Cho hình thang cân ABCD (AB//CD). Giả sử AB≤ CD, chọn câu đúng.

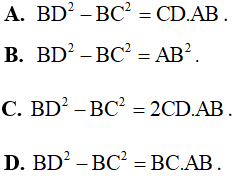
Giải

Kẻ 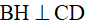tại H, 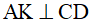tại K.

Áp dụng nhận xét về hình thang có hai cạnh bên song song vào hình thang ABHK có hai cạnh bên AK//BH nên AB = HK.

Xét hai tam giác vuông ADK và BCH có:

AD = BC (ABCD là hình thang cân)

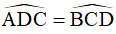(ABCD là hình thang cân)

Do đó: ΔADK=ΔBCH (cạnh huyền, góc nhọn). Suy ra DK = HC.

Xét tam giác vuông BDH, theo định lý Py-ta-go, ta có: .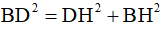

Xét tam giác vuông CBH, theo định lý Py-ta-go, ta có: .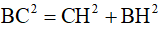

Suy ra

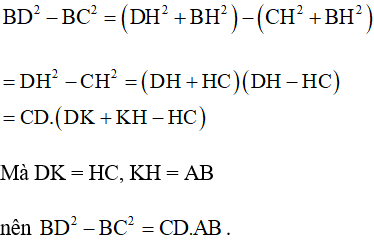
Đáp án: A.