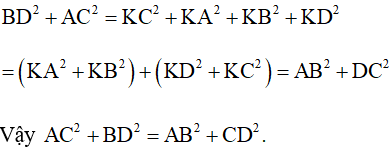Chứng minh hệ thức trong tứ giác hay, chi tiết
Chứng minh hệ thức trong tứ giác hay, chi tiết
Tài liệu Chứng minh hệ thức trong tứ giác hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
A. Phương pháp giải.
Chứng minh quan hệ về độ dài:
- Sử dụng bất đẳng thức trong tam giác. Với là độ dài ba cạnh của một tam giác thì:
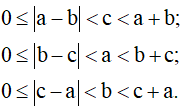
- Áp dụng định lý Pitago trong tam giác vuông.
B. Ví dụ minh họa
Ví dụ 1. Chứng minh rằng: Trong một tứ giác mỗi đường chéo nhỏ hơn nửa chu vi của tứ giác.
Giải
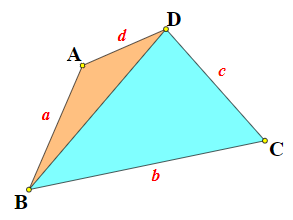
Đặt độ dài các cạnh như hình vẽ thì nửa chu vi của tứ giác ABCD là:
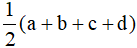
Áp dụng bất đẳng thức tam giác vào hai tam giác ABD và BCD, ta được:
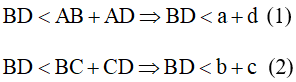
Từ (1) và (2) suy ra
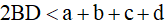
hay
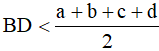
Chứng minh tương tự, ta cũng được
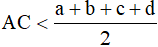
Vậy mỗi đường chéo nhỏ hơn nửa chu vi của tứ giác.
Ví dụ 2. Chứng minh rằng: Trong một tứ giác tổng hai đường chéo lớn hơn tổng hai cạnh đối.
Giải
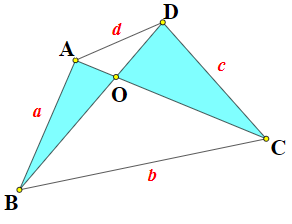
Gọi O là giao điểm của AC và BD.
Áp dụng bất đẳng thức tam giác vào hai tam giác chứa hai cạnh đối nhau AB, CD là OAB, OCD ta được:
OA + OB > AB hay OA + OB > a (1)
OC + OD > CD hay OC + OD > c (2)
Từ (1) và (2) suy ra: OA + OB + OC + OD > a + c ⇒ AC + BD > a + c
Chứng minh tương tự, ta cũng được AC + BD > b + d
Vậy tổng hai đường chéo lớn hơn tổng hai cạnh đối.
Ví dụ 3. Chứng minh rằng: Trong một tứ giác tổng hai đường chéo lớn hơn nửa chu vi nhưng nhỏ hơn chu vi của tứ giác ấy.
Giải
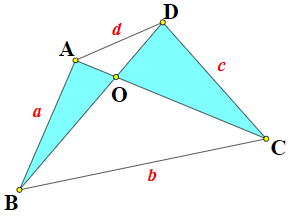
Giả sử tứ giác ABCD có AB = a, BC = b, CD = c, DA = d. Gọi O là giao điểm của AC, BD ta có: AC + BD = AO + OB + OC + OD > AB + CD = a + c (bất đẳng thức tam giác)
Tương tự ta chứng minh được: AC + BD > b + d
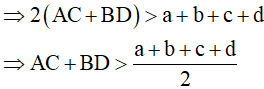
Vậy tổng hai đường chéo lớn hơn nửa chu vi của tứ giác.
Theo bất đẳng thức tam giác ta có:
AC < AB + BC = a + b; AC < AD + DC = c + d
BD < AB + AD = a + d; BD < BC + CD = b + c
⇒2AC + 2BD < 2a + 2b + 2c + 2d
⇒AC + BD < a + b + c + d.
Vậy tổng hai đường chéo nhỏ hơn chu vi tứ giác.
Ví dụ 4. Tứ giác ABCD có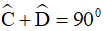 
. Chứng minh rằng: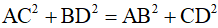
Giải
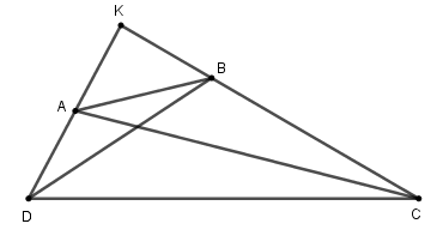
Gọi K là giao điểm của AD và BC.
Vì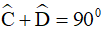 
nên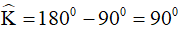 
(định lý tổng ba góc của tam giác)
Áp dụng định lý Pyatgo
Xét ΔKAC vuông tại K ta có: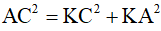 
Xét ΔKBD vuông tại K ta có: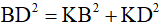 
Xét ΔKAB vuông tại K ta có: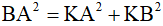 
Xét ΔKCD vuông tại K ta có: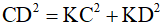 
Từ đó
