Cách chứng minh đa thức chia hết cho đơn thức, đa thức
Cách chứng minh đa thức chia hết cho đơn thức, đa thức
Tài liệu Cách chứng minh đa thức chia hết cho đơn thức, đa thức Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
+ Để chứng minh một phép chia là phép chia hết, ta cần chứng minh phần dư của phép chia bằng 0.
+ Chú ý: xn : xm = xn-m
+ Muốn chia một đa thức cho một đơn thức ta lấy từng hạng tử của đa thức chia cho đơn thức.
B. Ví dụ minh họa
Ví dụ 1: Tìm số tự nhiên n để đa thức A chia hết cho đơn thức B với:
A = 7xn-1y5 - 5x3y4; B = 5x2yn

Giải:
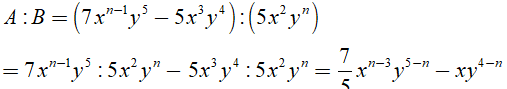
Theo đề bài đa thức A chia hết cho đơn thức B
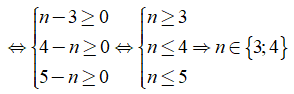
Vậy giá trị n cần tìm là 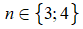
Chọn A.
Ví dụ 2. Cho phép chia: (x3 + 9x2 + 27x + 27) : (x + 3). Tìm khẳng định sai?
A. Đây là phép chia hết
B. Thương của phép chia là: (x+ 3)2
C. Thương của phép chia là : x2 + 6x + 9
D. Số dư của phép chia là x – 3 .
Lời giải
Áp dụng hằng đẳng thức đáng nhớ:
(a + b)3 = a3 + 3a2b + 3ab2 + b3 ta được:
(x3 + 9x2 + 27x + 27) : (x + 3) = (x + 3)3 : (x + 3) = (x+ 3)2 = x2 + 6x +9
Vậy phéo chia đã cho là phép chia hết có thương là: (x+ 3)2 = x2 + 6x + 9.
Chọn D.
Ví dụ 3. Thực hiện phép chia: ( x2y + 4xy + 3y ) : (x + 1) ta được thuơng là:
A. xy + 3 B. x +3y C. x + y + 3 D. y. (x + 3)
Lời giải
Ta có: x2y + 4xy + 3y = y.(x2 + 4x +3)
= y . [ (x2 + x )+ (3x+ 3)]
= y .[ x. (x+ 1) + 3(x+ 1)]
= y. (x + 3). (x+1 )
Vậy : ( x2y + 4xy + 3y ) : (x + 1) = y. ( x+ 3). (x+ 1) : (x+1) = y. (x+ 3).
Chọn D.
Ví dụ 4. Tìm a để phép chia (x3 – 4x + a): (x – 2) là phép chia hết:
A. a = 0 B. a = 4 C. a = -8 D. a = 8
Lời giải
Ta có:
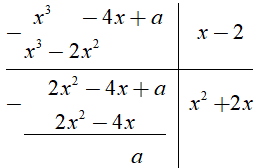
Để phép chia đã cho là phép chia hết khi và chỉ khi phần dư bằng 0 . Do đó, a =0
Chọn A.
C. Bài tập trắc nghiệm
Câu 1. Ta có: (2x3 - 26x - 24):(x2 + 4x + 3) = ax + b. Tính a + b?
A. 6 B. -3 C. -6 D. 10
Ta có phép chia
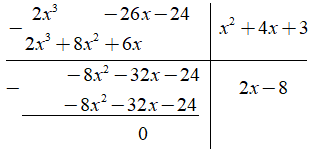
Vậy (2x3 - 26x - 24) = (x2 + 4x + 3)(2x - 8)
Suy ra: a= 2; b = -8 nên a + b = - 6
Chọn C
Câu 2. Tìm a để phép chia sau là phép chia hết: (x3 - 9x2 + 28x -a):(x - 3)
A.a = 30 B. a = -30 C. a = 60 D. a = - 60
Ta có phép chia
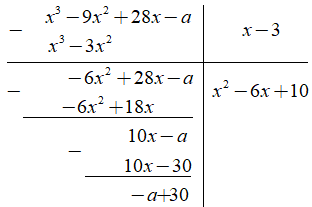
Để phép chia đã cho là phép chia hết khi -a + 30 = 0 nên a= 30.
Chọn A.
Câu 3. Tìm số tự nhiên n nhỏ nhất để phép chia sau là phép chia hết: (7xn-2y5 + 8x8yn+1):x3y5
A.n = 3 B. n = 4 C. n = 6 D .n = 5
(7xn-2y5 + 8x8yn+1):x3y5
= 7xn-2y5 : x3y5 + 8x8yn+1 : x3y5
= 7xn-5 + 8x5yn-4
Để phép chia đã cho là phép chi hết khi và chỉ khi:
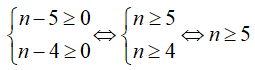
Do đó, số tự nhiên nhỏ nhất thỏa mãn là n = 5
Chọn D.
Câu 6. Tìm số nguyên n lớn nhất để phép chia sau là phép chia hết :
(-4x3-ny8 + 12x10y8-2n):x5y6
A. n =-1 B. n = -2 C. n = -3 D. n = -4
(-4x3-ny8 + 12x10y8-2n):x5y6
= -4x3-ny8 : x5y6 + 12x10y8-2n : x5y6
= -4x-2-ny2 + 12x5y2-2n
Để phép chia đã cho là phép chia hết khi và chỉ khi:
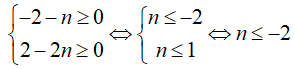
Do đó, số nguyên n lớn nhất để phép chia đã cho là phép chia hết là n = -2
Chọn B.
Câu 7. Chứng minh đa thức 2x2y - 2axy - x2 + ax - xy + ay luôn chia hết cho đa thức ( x – a) với mọi giá trị của a.
2x2y - 2axy - x2 + ax - xy + ay
= (2x2y - 2axy) - (x2 - ax) - (xy - ay)
= 2xy.(x - a) - x(x - a) - y(x - a)
= (x - a).(2xy - x - y)
Suy ra, đa thức 2x2y - 2axy - x2 + ax - xy + ay luôn chia hết cho ( x – a)
Câu 8. Chứng minh đa thức 2x2 - 2y2 - 2ax + 2ay luôn chia hết cho đa thức ( x + y – a) với mọi giá trị của a.
Ta có:
2x2 - 2y2 - 2ax + 2ay = (2x2 - 2y2) - (2ax - 2ay)
= 2(x2 - y2) - 2a(x - y)
= 2(x + y).(x - y) - 2a(x - y)
= 2(x - y).(x + y - a)
Do đó, đa thức 2x2 - 2y2 - 2ax + 2ay luôn chia hết cho đa thức ( x + y – a) với mọi giá trị của a.

