Vận dụng các trường hợp đồng dạng trong tam giác vuông chứng minh hệ thức
Vận dụng các trường hợp đồng dạng trong tam giác vuông chứng minh hệ thức
Tài liệu Vận dụng các trường hợp đồng dạng trong tam giác vuông chứng minh hệ thức Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
Dạng bài: Chứng minh hệ thức hình học
A. Ví dụ minh họa
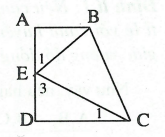Câu 1: Hình thang vuông ABCD có 
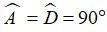, AB = 6cm, CD = 12cm,, AD = 17cm. Lấy điểm E trên cạnh AD sao cho AE = 8cm.
a. Hỏi ΔABE đồng dạng với tam giác nào? Vì sao?
b. Chứng minh rằng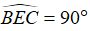 
.
Lời giải:
a. Xét hai tam giác vuông ΔABE và ΔDEC, ta có:
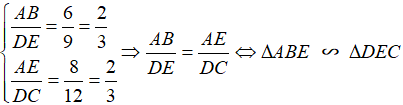
b. Theo kết quả câu a), ta suy ra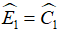 
.
Mặt khác trong ΔCDE vuông tại D, ta có: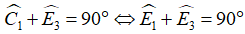 
.
Khi đó:
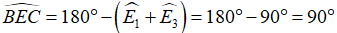
Câu 2: Cho ΔABC vuông tại A, đường cao AH. Chứng minh rằng:
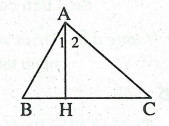
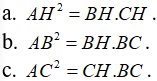
Lời giải:
a. Xét hai tam giác vuông ΔAHB và ΔAHC, ta có:
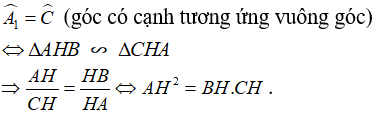
b. Xét hai tam giác vuông ΔAHB và ΔACB, ta có:
c. Xét hai tam giác vuông ΔAHC và ΔACB, ta có:
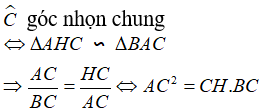
Câu 3: Cho hình bình hành ABCD có AC > BD. Kẻ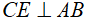 
tại E, 
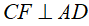tại F, 
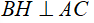tại H và 
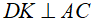tại K. Chứng minh:
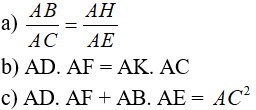
Lời giải:
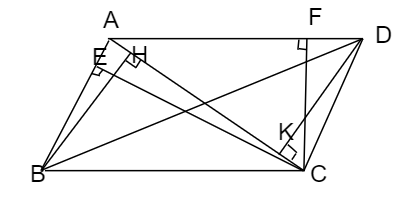
a) Xét hai tam giác vuông AHB và AEC có :
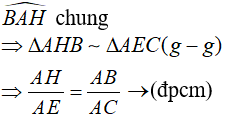
b) Xét hai tam giác vuông AKD và AFC có :
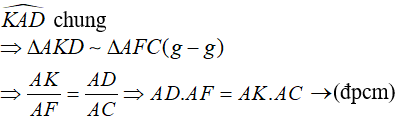
c) Vì ABCD là hình bình hành
B. Bài tập tự luyện
Câu 1: Cho tam giác ABC (AB < AC), hai đường cao BE và CF gặp nhau tại H, các đường thẳng kẻ từ B song song với CF và từ C song song với BE gặp nhau tại D. Chứng minh
a) ΔABE đồng dạng ΔACF
b) AE. CB = AB. EF
c) Gọi I là trung điểm của BC. Chứng minh H, I, D thẳng hàng.
Câu 2: Cho tam giác ABC có các góc đều nhọn. Các đường cao AD, BE, CF cắt nhau ở H.
a) CMR: AE. AC = AF. AB
b) CMR: ΔAFE đồng dạng ΔACB
c) CMR: ΔFHE đồng dạng ΔBHC
d) CMR: BF. BA + CE. CA = BC2
Câu 3: Cho tam giác ABC vuông tại A, có AB = 6cm; AC = 8cm. Vẽ đường cao AH (H ∈ BC)
a) Tính độ dài cạnh BC.
b) Chứng minh tam giác HBA đồng dạng với tam giác ABC.
c) Vẽ phân giác AD của góc A (D ∈ BC). Chứng minh rằng điểm H nằm giữa hai điểm B và D.
Câu 4: Cho hình bình hành ABCD. Gọi hình chiếu của A trên CD là H, hình chiếu của A trên BC là K.
a. Chứng minh rằng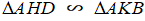 
.
b. Hình bình hành ABCD có thêm điều kiện gì thì các tam giác AHC và AKC đồng dạng với nhau?
Câu 5: Cho hình vuông ABCD. Trên cạnh AB lấy điểm M. Kẻ BH vuông góc với CM, nối DH. Vẽ HN vuông góc với DH (N thuộc BC). Chứng minh rằng:
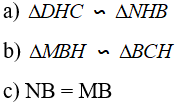
Câu 6: Cho tam giác ABC nhọn và đường cao AH. Kẻ HI vuông góc với AB và HK vuông góc với AC.
Câu 7: Cho hình chữ nhật ABCD có AB > AD và AD = 5cm. Trên DC lấy điểm M sao cho DM = 2cm. Biết góc AMB là 900.
a) Chứng minh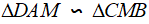 
. Tính MC.
b) Tia phân giác của góc AMB cắt AB tại E. Kẻ EK vuông góc với AB (K ∈ MB)
Chứng minh EA = EK.
c) Tia EK cắt AM tại H, tia AK cắt BH tại N. Chứng minh MN là tia phân giác của góc BMH.
