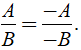Lý thuyết Tính chất cơ bản của phân thức hay, chi tiết

Lý thuyết Tính chất cơ bản của phân thức hay, chi tiết

Haylamdo biên soạn và sưu tầm Lý thuyết Tính chất cơ bản của phân thức hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Lý thuyết

1. Tính chất cơ bản của phân thức

+ Nếu nhân cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

(M là một đa thức khác đa thức 0)

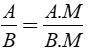
+ Nếu chia cả tử và mẫu của một phân thức với cùng một đa thức khác đa thức không thì được một phân thức bằng phân thức đã cho.

(M là một đa thức khác đa thức 0)

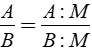
Ví dụ: Cho phân thức (2x)/(x + 2). Nhân cả tử và mẫu với đa thức ( x - 1 ), so sánh phân thức nhận được với phân thức đã cho ?

Hướng dẫn:

Ta có phân thức mới là

Ta có 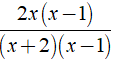= (2x)/(x + 2) vì 2x( x - 1 ).( x + 2 ) = 2x.( x + 2 )( x - 1 ).

2. Quy tắc đổi dấu

Nếu đổi dấu cả tử và mẫu của một phân thức thì nhận được phân thức mới bằng phân thức đã cho.

Ta có thể viết như sau:

Ví dụ: Ta có phân thức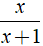 . Đổi dấu cả tử và mẫu ta được phân thức mới, so sánh phân thức mới với phân thức đã cho

Hướng dẫn:

Ta có phân thức mới nhận được là.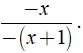

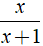
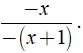
Ta có: = vì x. - ( x + 1 ) = - x.( x + 1 ).

B. Bài tập tự luyện

Bài 1: Hai phân thức sau có bằng nhau không ?

a, (x² - 2x)/(x² - 4) và x/(x + 2).

b, (x + 1)/(x + 3) và (x² + 3x + 2)/(x² - x - 6)

Hướng dẫn:

a) Ta có: ( x² - 2x )( x + 2 ) = x( x - 2 )( x + 2 ).

Mà x( x² - 4 ) = x( x - 2 )( x + 2 )

Vậy hai phân thức đó bằng nhau.

b) Ta có ( x + 1 )( x² - x - 6 ) = ( x + 1 )( x - 3 )( x + 2 ).

Nhưng ( x + 3 )( x² + 3x + 2 ) = ( x + 2 )( x + 1 )( x + 3 )

Vậy hai phân thức đó không bằng nhau.

Bài 2: Chứng minh các đẳng thức sau:

a, (x³ - 1)/(x - 1) = x² + x + 1

b, (x⁵ - 1)/(x² - 1) = (x⁴ + x³ + x² + x + 1)/(x + 1)

Hướng dẫn:

a) Ta có: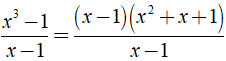 = x² + x + 1

⇒ (x³ - 1)/(x - 1) = x² + x + 1 (đpcm).

b) Ta có: ( x⁵ - 1 )( x + 1 ) = x⁶ + x⁵ - x - 1

Mặt khác, ta có: ( x² - 1 )( x⁴ + x³ + x² + x + 1 ) = ( x⁶ + x⁵ + x⁴ + x³ + x² ) - ( x⁴ + x³ + x² + x + 1 )

= x⁶ + x⁵ - x - 1.

⇒ (x⁵ - 1)/(x² - 1) = (x⁴ + x³ + x² + x + 1)/(x + 1) (đpcm)