Chứng minh hai tam giác vuông đồng dạng hay, chi tiết
Chứng minh hai tam giác vuông đồng dạng hay, chi tiết
Tài liệu Chứng minh hai tam giác vuông đồng dạng hay, chi tiết Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.
Dạng bài: Chứng minh hai tam giác vuông đồng dạng
A. Phương pháp giải
Hai tam giác vuông đồng dạng với nhau nếu:
Tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia.
Tam giác vuông này có hai cạnh góc vuông tỉ lệ với hai cạnh góc vuông của tam giác vuông kia.
Định lí: Nếu cạnh huyền và cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác kia thì hai tam giác vuông đó đồng dạng.
Như vậy, nếu hai tam giác vuông ΔABC và ΔA1B1C1 thỏa mãn:
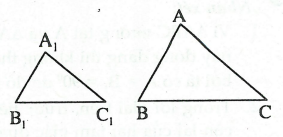
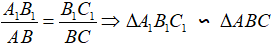
Và khi đó ta có :
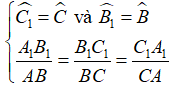
Định lí: Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
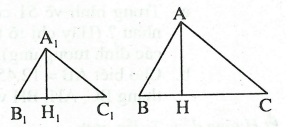Như vậy, nếu 
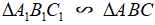với tỉ số k thì
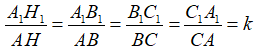
Và khi đó ta có thêm:
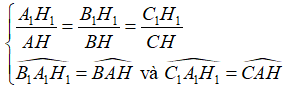
Định lí: Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Như vậy, nếu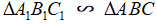 
với tỉ số k thì 
.
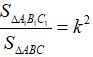B. Ví dụ minh họa
Câu 1: Cho ΔABC vuông tại A, AC = 8cm, BC = 12cm. Kẻ tia Cx vuông góc với BC. Trên Cx lấy điểm D sao cho BD =18cm. Chứng minh rằng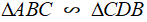 
.
Lời giải:
Xét hai tam giác vuông ΔABC và ΔBCD, ta có:
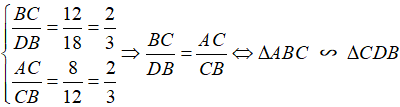
Câu 2: Cho tam giác ABC, phân giác AD. Gọi E và F lần lượt là hình chiếu của B và C lên AD. Chứng minh rằng: AE.DF=AF.DE
Lời giải:
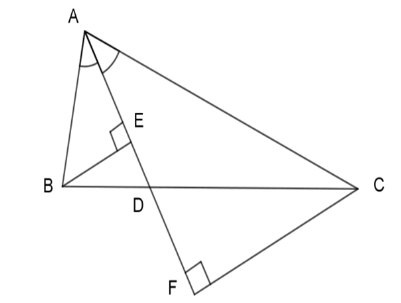
Xét hai tam giác vuông ABE và ACF có:
Xét hai tam giác vuông BDE và CDF có:
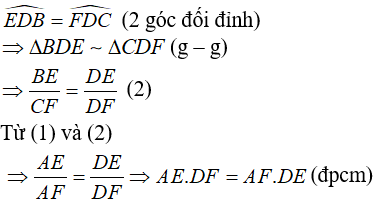
Câu 3: Cho tam giác nhọn ABC có đường cao CK. Dựng ra phía ngoài tam giác ABC hai tam giác ACE và CBF tương ứng vuông góc tại E; F và thỏa mãn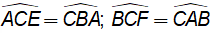 
. Chứng minh rằng: 
.
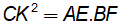Lời giải:
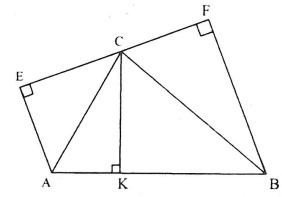
Xét ΔACK và ΔBCF có:
C. Bài tập tự luyện
Câu 1: Cho tam giác ABC vuông ở A, đường cao AH. Chứng minh rằng:
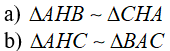
Câu 2: Cho hai tam giác vuông ABC và ABD có đỉnh góc C và D nằm trên một nửa mặt phẳng bờ AB. Gọi P là giao điểm của các cạnh AC và BD. Đường thẳng qua P vuông góc với AB tại I. Chứng minh rằng:
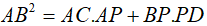
Câu 3: Cho tam giác ABC nhọn có BD và CE là hai đường cao cắt nhau tại H. Gọi M là giao điểm của AH và BC. Chứng minh rằng:
MH.MA=MB.MC
Câu 4: Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H.
a) Chứng minh rằng H là giao điểm các đường phân giác trong tam giác DEF.
b) Gọi K là giao điểm của AD và EF. Chứng minh rằng: HK.AD=AK.DH
Câu 5: Kẻ đường cao BD và CE của tam giác ABC và các đường cao DF và EG của tam giác ADE.
a) Chứng minh AD. AE = AB. AG = AC. AF
b) Chứng minh FG//BC.
Câu 6: Cho tam giác ABC vuông tại A. Điểm D trên cạnh AC. Đường thẳng qua D vuông góc với BC tại E cắt AB tại F. Chứng minh rằng:
a) DAF ∽ DEC
b) ABC ∽ EDC.
Câu 7: Giả sử AC là đường chéo lớn của hình bình hành ABCD. Từ điểm C hạ các đường vuông góc CE và CF tương ứng trên đường kéo dài của các cạnh AB và AC. Chứng minh rằng AB.AE + AD.AF = AC2.
