Các dạng toán về đường thẳng song song với đường thẳng cho trước và cách giải

Các dạng toán về đường thẳng song song với đường thẳng cho trước và cách giải

Tài liệu Các dạng toán về đường thẳng song song với đường thẳng cho trước và cách giải Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

I. Lý thuyết

1. Định nghĩa khoảng cách giữa hai đường thẳng song song

Khoảnh cách giữa hai đường thẳng song song là khoảng cách giữa một điểm tùy ý trên đường thẳng này đến đường thẳng kia.

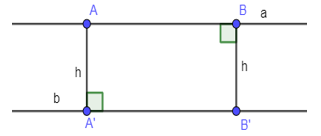
Cho hai đường thẳng a và b song song với nhau. Khi đó trên đường thẳng a lấy điểm A và trên b lấy điểm B’.

Vẽ AA^' ⊥ b (A^' ∈ b); BB^' ⊥ a (B ∈ a). Khoảng cách từ đường thẳng a đến đường thẳng b là đoạn AA’ hoặc BB’.

2. Tính chất chất các điểm cách đều một đường thẳng cho trước

Các điểm cách đường thẳng b một khoảng bằng h thì nằm trên đường thẳng song song với b và cách b một khoảng bằng h.

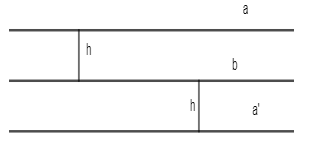
a // b // a’

a và a’ cách b một khoảng bằng h.

Nhận xét: Tập hợp các điểm cách một đường thẳng cố định một khoảng bằng h không đổi là hai đường thẳng song song với đường thẳng đó và cách đường thẳng đó một khoảng bằng h.

3. Ghi chú

- Tập hợp các điểm cách điểm O cố định một khoảng bằng r không đổi là đường tròn (O;r)

- Tập hợp các điểm cách đều hai đầu mút của đoạn một đoạn thẳng cố định là đường trung trực của đoạn thẳng đó.

- Tập hợp các điểm nằm trong góc và cách đều hai cạnh của góc là tia phân giác của góc đó.

II. Dạng bài tập và phương pháp giải

Dạng 1: Phát biểu tập hợp điểm không chứng minh

Phương pháp giải: Vận dụng các tính chất để chỉ ra hình dạng của tập hợp các điểm cùng thỏa mãn một điều kiện nào đó.

Ví dụ: Điền vào chỗ chấm

a) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 2cm là ...

b) Tập hợp đỉnh A các tam giác vuông ABC có cạnh huyền BC cố định và BC = 4cm là ...

c) Tập hợp giao điểm O của hai đường chéo của hình chữ nhật ABCD có cạnh BC cố định là ...

Lời giải:

a) Tập hợp các điểm cách đều đường thẳng a cố định một khoảng 2cm là hai đường thẳng song song với đường thẳng a và cách đều đường thẳng a một khoảng 2cm.

b) Tập hợp đỉnh A các tam giác vuông ABC có cạnh huyền BC cố định và BC = 4cm là đường tròn tâm O bán kính 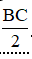với O là trung điểm của BC và bỏ đi hai điểm B, C.

c) Tập hợp giao điểm O của hai đường chéo của hình chữ nhật ABCD có cạnh BC cố định là đường trung trực của đoạn BC trừ hai điểm B, C.

Dạng 2: Vận dụng kiến thúc về đường thẳng song song với đường thẳng cho trước để chứng minh bài toàn.

Phương pháp giải: Vận dụng lí thuyết và định lý để chứng minh bài toán.

Ví dụ: Cho tam giác ABC nhọn, các đường cao BD, CE. Gọi H, K lần lượt là các chân đường cao kẻ từ B và C đến DE. Chứng minh: HE = DK

Lời giải:

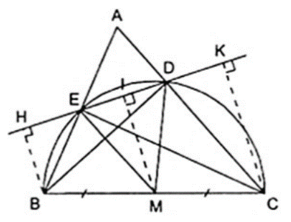
Vì BD, CF là đường cao của tam giác ABC nên

Do đó BDC vuông tại D, ΔCEB vuông tại E.

Gọi M là trung điểm của BC.

=> DM, EM là đường trung tuyến ứng với cạnh huyền ΔBDC và ΔCEB

Áp dụng tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông ta được:

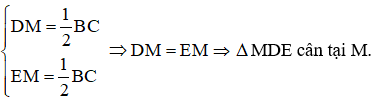
Từ giả thuyết ta có tứ giác BHKC là hình thang vuông nên vẽ MI DE thì BH // MI //CK (1) (vì cùng vuông góc với đường thẳng DE).

Mà ta có: BM = MC (2) (do ta vẽ hình trên)

Từ (1), (2) => BH, MI, CK là ba đường thẳng song song và cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK (3)

Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được MI là đường trung tuyến của tam giác MDE

=> I là trung điểm của ED

=> EI = ID (4)

Trừ theo vế đẳng thức (3) cho (4) ta được: HI – EI = IK – ID

Hay HE = DK.

Dạng 3: Tìm quỹ tích

Phương pháp giải: Vận dụng các nhận xét về tập hợp điểm.

Ví dụ: Cho tam giác ABC và một điểm M nằm trên cạnh BC. Khi điểm M di chuyển trên BC thì trung điểm I của AM di chuyển trên đường nào.

Lời giải:

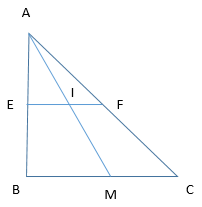
Gọi E, F là trung điểm của AB và AC. Ta sẽ chứng minh E, I, F thẳng hàng.

Do E, I lần lượt là trung điểm của AB và AM nên EI là đường trung bình của tam giác ABM

=> EI //BM EI // BC (1)

Do F, I lần lượt là trung điểm của AC và AM nên IF là đường trung bình của tam giác AMC

=> IF // MC FI // BC (2)

Từ (1) và (2) => E, I, F thẳng hàng

Mà E là trung điểm AB, F là trung điểm AC nên EF là đường trung bình của tam giác ABC

Mà E, F cố định do AB, AC cố định

Nên khi M di chuyển trên BC thì trung điểm I của AM di chuyển trên EF là đường trung bình của tam giác ABC.

III. Bài tập tự luyện

Bài 1: Điền vào chỗ chấm.

a) Tập hợp các điểm cách điểm A cố định một khoảng cho trước bằng 1cm là ...

b) Tập hợp các điểm cách đều hai đầu đoạn thẳng AB cố định là ...

c) Tập hợp các điểm nằm trong góc xOy và cách đều hai cạnh của góc là ...

Bài 2: Cho tam giác ABC và một điểm M nằm trên cạnh BC. Qua M ta kẻ đường thẳng song song với cạnh AB, cắt cạnh AC tại điểm E và đường thẳng song song với cạnh AC, cắt cạnh AB tại D. Khi M di chuyển trên BC thì trung điểm I của đoạn thẳng DE di chuyển trên đường nào?

Bài 3: Cho tam giác ABC cân tại A. Các điểm D, E theo thứ tự di chuyển trên AB, AC sao cho AD = AE. Trung điểm I của đoạn thẳng DE di chuyển trên đường nào?

Bài 4: Cho đoạn thẳng AB, điểm M chuyển động trên đoạn thẳng AB. Vẽ về cùng một phía của nửa mặt phẳng bờ AB các tam giác đều AMC và BMD. Trung điểm I của đoạn thẳng CD di chuyển trên đường nào?

Bài 5: Cho đoạn thẳng AB, điểm M chuyển động trên đoạn thẳng AB. Vẽ về một phía của nửa mặt phẳng bờ AB các tam giác AMC vuông cân tại C và BMD vuông cân tại D. Trung điểm I của đoạn CD di chuyển trên đường nào.

Bài 6: Cho tam giác ABC có D là trung điểm của AB, kẻ DE // BC ( E thuộc AC). Chứng minh AE = EC.

Bài 7: Cho tam giác ABC có trọng tâm G, E là trung điểm của AG, các đường thẳng song song với BC và qua E và G lần lượt cắt AB tại các điểm F và H. Chứng minh AF = FH = HB.

Bài 8: Cho tam giác ABC vuông tại A, M là một điểm thuộc cạnh BC. Gọi E và D lần lượt là chân các đường vuông góc kẻ từ M đến AB, AC. Tìm vị trí điểm M trên BC sao cho độ dài DE nhỏ nhất.

Bài 9: Cho đoạn thẳng AB. Kẻ tia Ax bất kỳ. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE. Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra ba phần bằng nhau.

Bài 10: Cho đoạn thẳng AB kẻ tia Ax bất kỳ. Trên Ax lấy các điểm C, D, E sao cho AC = CD = DE. Nối E với B. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia thành ba đoạn bằng nhau.