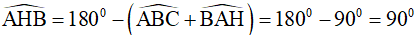Chứng minh hai góc bằng nhau, tính số đo góc trong hình bình hành
Chứng minh hai góc bằng nhau, tính số đo góc trong hình bình hành
Tài liệu Chứng minh hai góc bằng nhau, tính số đo góc trong hình bình hành Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
1. Vẽ thêm hình bình hành bằng cách xác định một đoạn thẳng có trung điểm làm một đường chéo, sau đó chọn một trong hai giải pháp sau:
- Vẽ thêm đường chéo thứ hai.
- Kẻ thêm đường thẳng song song.
2. Áp dụng định lí đường trung bình của tam giác, định lý tổng ba góc trong tam giác, tổng các góc trong tứ giác.
3. Sử dụng tính chất cặp góc ở vị trí đồng vị hoặc so le của hai đường thẳng song song.
4. Sử dụng các tính chất của hình bình hành:
- Hai góc đối bằng nhau
- Hai đường chéo cắt nhau tại trung điểm của mỗi đường
- Các cặp cạnh đối song song và bằng nhau.
B. Ví dụ minh họa
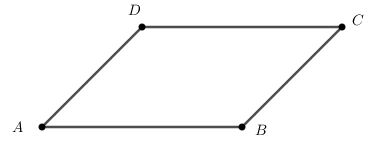
Ví dụ 1. Cho hình bình hành ABCD có 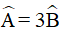 . Số đo các góc của hình bình hành là:
. Số đo các góc của hình bình hành là:
Giải
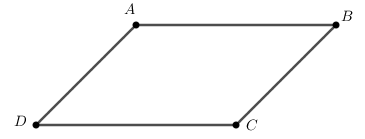
Trong hình bình hành ABCD có: 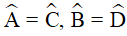 (tính chất),
(tính chất), 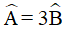 (gt)
(gt)
Theo định lí tổng các góc trong tứ giác ta có:
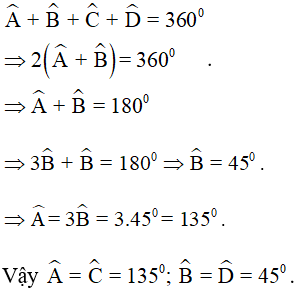
Ví dụ 2. Tính số đo các góc của hình bình hành ABCD biết 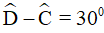 .
.
Giải
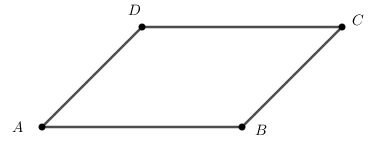
Trong hình bình hành ABCD có: 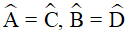 (tính chất),
(tính chất),
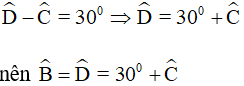
Theo định lí tổng các góc trong tứ giác ta có:
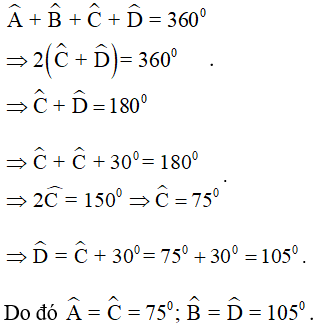
Ví dụ 3. Cho tam giác ABC (AC < AB) có 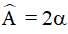 . Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E, F lần lượt là trung điểm của AD, BC. Tính góc BEF
. Trên cạnh AB lấy điểm D sao cho BD = AC. Gọi E, F lần lượt là trung điểm của AD, BC. Tính góc BEF
Giải
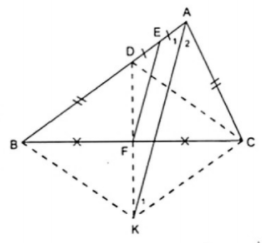
Do F là trung điểm của BC theo giả thiết nên chọn BC là một đường chéo. Vẽ thêm điểm K sao cho F là trung điểm của DK thì tứ giác BDCK có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành. Kết hợp với E là trung điểm của AD ta có FE là đường trung bình của ΔADK .
Áp dụng tính chất về cạnh vào hình bình hành BDCK và giả thiết, ta được:
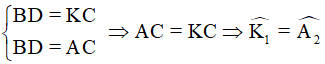
(vì trong một tam giác, đối diện với hai cạnh bằng nhau là hai góc bằng nhau). (1)
Lại có 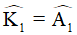 , (vì AB // CK, hai góc ở vị trí so le trong). (2)
, (vì AB // CK, hai góc ở vị trí so le trong). (2)
Từ (1), (2) suy ra
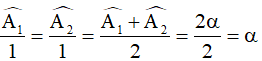
Áp dụng định lí đường trung bình vào ΔADK ta được FE//KA.
Vậy 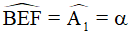 vì là góc đồng vị của FE//KA.
vì là góc đồng vị của FE//KA.
C. Bài tập vận dụng
Câu 1. Hãy chọn câu đúng. Tứ giác ABCD là hình bình hành nếu

Câu 2. Tính các góc của hình bình hành ABCD biết: 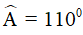 .
.
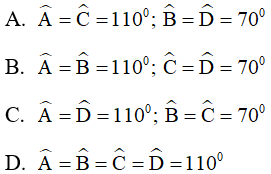
Câu 3. Tính các góc của hình bình hành ABCD biết: 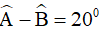 .
.
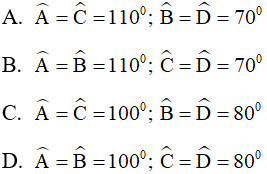
Câu 4. Cho hình bình hành ABCD có 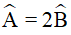 số đo các góc của hình bình hành là:
số đo các góc của hình bình hành là:
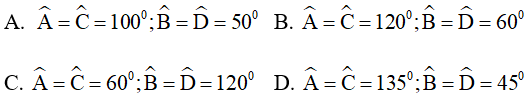
Câu 5. Tính số đo các góc của hình bình hành ABCD biết 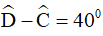 . Ta được:
. Ta được:
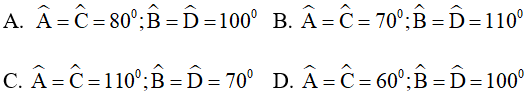
Câu 6. Hai góc kề nhau của một hình bình hành không thể có số đo là:
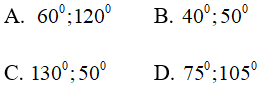
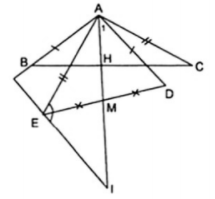
Câu 7. Cho tam giác ABC có góc A tù. Trong góc A vẽ các đoạn thẳng AD, AE sao cho AD vuông góc và bằng AB, AE vuông góc và bằng AC. Gọi M là trung điểm của DE, H là giao điểm của AM và BC. Tính 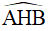
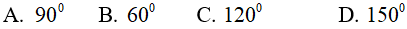

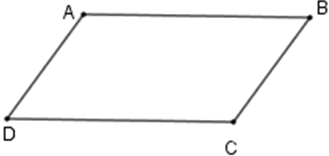
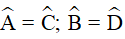 nên D đúng.
nên D đúng.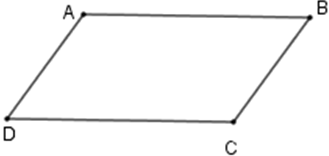
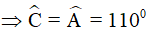 (tính chất hình bình hành)
(tính chất hình bình hành)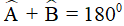 (2 góc trong cùng phía bù nhau)
(2 góc trong cùng phía bù nhau)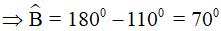
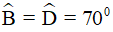 (tính chất hình bình hành)
(tính chất hình bình hành)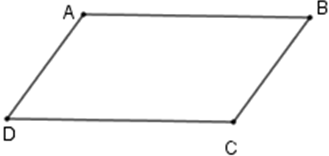
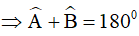 (2 góc trong cùng phía bù nhau)
(2 góc trong cùng phía bù nhau)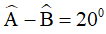 (gt)
(gt)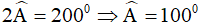
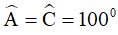 (tính chất hình bình hành)
(tính chất hình bình hành)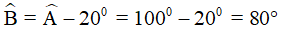
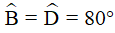 (tính chất hình bình hành)
(tính chất hình bình hành)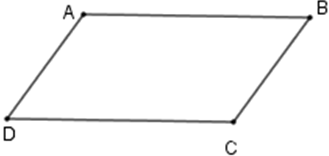
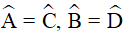 (tính chất) ,
(tính chất) , 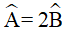
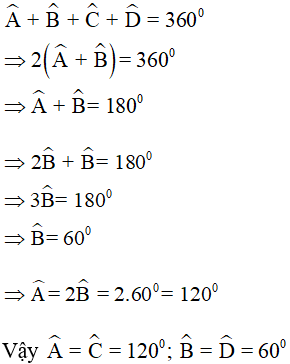
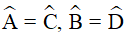 (tính chất),
(tính chất),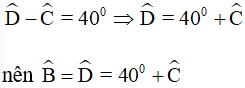
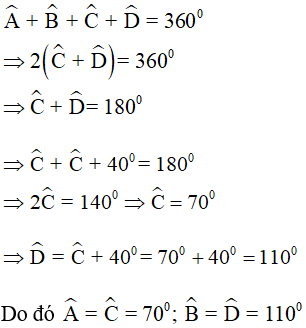
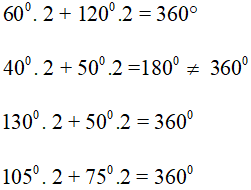
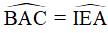 ( vì cùng bù với
( vì cùng bù với  )
)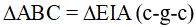 nên
nên 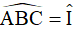 mà
mà 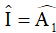 (EI//AD, 2 góc ở vị trí so le trong) nên ta có
(EI//AD, 2 góc ở vị trí so le trong) nên ta có 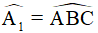 .
.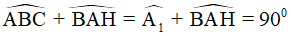 .
.