Tính giá trị biểu thức bằng cách sử dụng hằng đẳng thức cực hay
Tính giá trị biểu thức bằng cách sử dụng hằng đẳng thức cực hay
Tài liệu Tính giá trị biểu thức bằng cách sử dụng hằng đẳng thức cực hay Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

A. Phương pháp giải
Để tính giá trị của biểu thức ta cần:
+ Rút gọn biểu thức bằng cách sử dụng các hằng đẳng thức đáng nhớ, phép nhân đơn thức với đa thức, nhân đa thức với đa thức.
+ Sau đó, thay các giá trị tương ứng của biến vào biểu thức.
B. Ví dụ minh họa
Ví dụ 1. Tính giá trị biểu thức A = (2x - 2)(x2 + x + 1) - (x - 1)(x + 1) tại x = 10
A. 1899 B. 1891 C. 1991 D. 2001
Lời giải
Ta có:
A = (2x - 2)(x2 + x + 1) - (x - 1)(x + 1)
A = 2(x - 1)(x2 + x + 1) - (x2 - 1)
A = 2(x3 - 1) - x2 + 1
A = 2x3 - 2 - x2 + 1
A = 2x3 - x2 - 1
Giá trị của biểu thức với x= 10 là:
A = 2.103 - 102 - 1 = 2.1000 - 100 - 1
A = 1900 - 1 = 1899
Chọn A.
Ví dụ 2. Tính giá trị của biểu thức A = 1992 - 1
A. 39999 B. 39600 C. 27800 D. 39990
Lời giải
Ta có: A = 1992 - 1 = 1992 - 12
A = (199- 1). (199+1) = 198. 200= 39600
Chọn B
Ví dụ 3. Tính giá trị biểu thức B = (x - 1)(x2 + 1) - (x + 1)3 tại x= 100
A. -20998 B. -328791 C. -29870 D. -40202
Lời giải
Ta có:
B = (x - 1)(x2 + 1) - (x + 1)3
B = x3 + x - x2 - 1 - (x3 + 3x2 + 3x + 1)
B = x3 + x - x2 - 1 - x3 - 3x2 - 3x - 1
B = -4x2 - 2x - 2
Giá trị biểu thức tại x = 100 là:
B = -4.1002 - 2.100 - 2 = -4.10000 - 200 - 2 = -40202
Chọn D.
Ví dụ 4. Tính giá trị biểu thức A = 153 - 53
A. 3250 B. 2480 C. 3200 D. 1650
Lời giải
Ta có:
A = 153 - 53 = (15 - 5)(152 + 15.5 + 52)
A = 10.(225 + 75 + 25) = 10.325 = 3250
Chọn A.
C. Bài tập trắc nghiệm
Câu 1. Tính giá trị của biểu thức 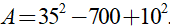
A. 252 B. 152 C. 452 D. 202
Ta có A = 352 -700 + +102 = 352 - 2.35.10 + 102.
Áp dụng hằng đẳng thức (a - b)2 = a2 - 2ab + b2
Khi đó A= (35 - 10)2 = 252
Chọn đáp án A.
Câu 2: Tính giá trị của biểu thức 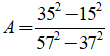
Ta có:
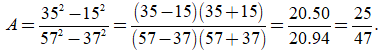
(áp dụng hằng đẳng thức a2 - b2 = (a - b)(a + b))
Vậy
Chọn A.
Câu 3. Tính giá trị biểu thức 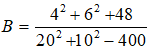
A. B = 2 B. B= 3 C. B = 1 D. B= 4
Ta có :
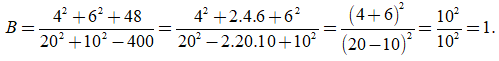
(áp dụng hằng đẳng thức (a + b)2 = a2 + 2ab + b2; (a - b)2 = a2 - 2ab + b2 )
Vậy B = 1
Chọn C.
Câu 4. Tính giá trị biểu thức A = (xy + y)(x - y) - y(x2 - y) với x = 1000 và y = 1
A. 0 B. 1000 C. -1000 D. 5000
A = (xy + y)(x - y) - y(x2 - y)
A = x2y - xy2 + xy - y2 - x2y + y2
A = -xy2 + xy = xy(-y + 1)
Tại y = 1 thì – y + 1 = -1 + 1= 0
Suy ra, tại x = 1000; y =1 thì giá trị của biểu thức đã cho là A = 1000.1 . 0= 0
Chọn A.
Câu 5. Tính giá trị của biểu thức A = (x - 2y)(x2 + 2xy + 4y2) - x(x2 + y) tại x = -32 và y= 2
A. -640 B. 320 C. 0 D. 160
A = (x - 2y)(x2 + 2xy + 4y2) - x(x2 + y)
A = x3 - (2y)3 - (x3 + xy)
A = x3 - 8y3 - x3 - xy
A = -8y3 - xy = -y(8y2 + x)
Tại x = -32 và y = 2 thì 8y2 + x = 8.22 + (-32) = 0 nên giá trị của biểu thức đã cho là 0.
Chọn C.
Câu 6. Tính giá trị biểu thức 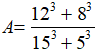
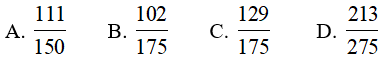
Ta có:
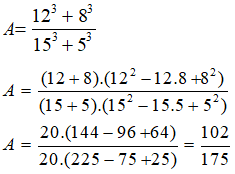
Chọn B.
Câu 7. Tính giá trị của biểu thức 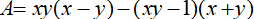
A. -15910 B. -12300 C. 23190 D. 12100
Ta có: A= xy ( x- y) – (xy – 1).(x+ y)
A = x2y - xy2 - (x2y + xy2 - x - y)
A = x2y - xy2 - x2y - xy2 + x + y
A = -2xy2 + x + y
Giá trị của biểu thức tại x = 80; y = 10 là
A = -2.80.102 + +80 + 10
A = -16000 + 90 = -15910
Chọn A
Câu 8. Tính giá trị của biểu thức A = x3 + 3xy(x + y) + y3 + 3x2 - 3y2 tại x = 8 và y = 2
A.1200 B. 1120 C. 1080 D. 1180
Ta có:
A = x3 + 3xy(x + y) + y3 + 3x2 - 3y2
A = x3 + 3x2y + 3xy2 + y3 + 3(x2 - y2)
A = (x + y)3 + 3(x + y)(x - y)
Giá trị của biểu thức tại x = 8 và y = 2 là:
A = (8 + 2)3 + 3(8 + 2)(8 - 2) = 103 + 3.10.6 = 1000 + 180 = 1180
Chọn D.
Câu 9. Tính giá trị biểu thức A = (x2 + y)(x - y) - x(x2 + y) + 10 tại x = 100; y = 1
A.-9991 B. -1001 C. -10001 D. -9999
Ta có:
A = (x2 + y)(x - y) - x(x2 + y) + 10
A = x3 - x2y + xy - y2 - x3 - xy + 10
A = -x2y - y2 + 10
Giá trị biểu thức tại x= 100; y =1 là:
A = -1002.1 - 12 + 10 = -10000 - 1 + 10 = -9991
Chọn A.
Câu 10. Tính giá trị biểu thức B = (x - xy)(xy - y) - xy(x + y) + (xy - 1)(xy + 1) tại x = 5; y= 20
A. 1001 B. -99 C. -101 D. -999
B = (x - xy)(xy - y) - xy(x + y) + (xy - 1)(xy + 1)
B = x2y - xy - x2y2 + xy2 - x2y - xy2 + x2y2 - 1
B = -xy - 1
Giá trị biểu thức tại x =5; y = 20 là:
B = -5.20- 1 = -100- 1 = -101
Chọn C.

