Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ nhất (C-C-C)

Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ nhất (C-C-C)

Tài liệu Chứng minh hai tam giác đồng dạng – trường hợp đồng dạng thứ nhất (C-C-C) Toán lớp 8 sẽ tóm tắt kiến thức trọng tâm về bài học từ đó giúp học sinh ôn tập để nắm vững kiến thức môn Toán lớp 8.

Dạng bài: Chứng minh hai tam giác đồng dạng theo trường hợp đồng dạng thứ nhất (c - c - c)

A. Phương pháp giải

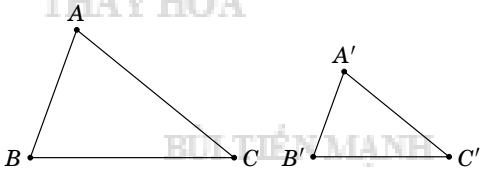Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

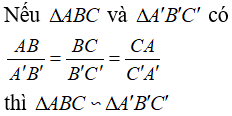
+) Xếp các cạnh của hai tam giác theo cùng một thứ tự (chẳng hạn từ nhỏ tới lớn).

+) Lập ba tỉ số, nếu chúng bằng nhau thì hai tam giác đồng dạng.

B. Ví dụ minh họa

Câu 1: Cho ΔABC vuông tại A có AB = 3cm, BC = 5cm và ΔA₁B₁C₁ vuông tại B₁ có A₁B₁ = 6cm, B₁C₁ = 8cm. Hỏi rằng hai tam giác vuông ΔABC và ΔA₁B₁C₁ có đồng dạng với nhau không? Vì sao?

Lời giải:

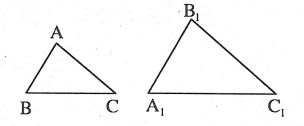Trong ΔABC vuông tại A, ta có:

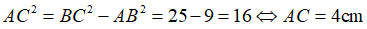
Trong ΔA₁B₁C₁ vuông tại B₁, theo Pi – ta – go, ta có:

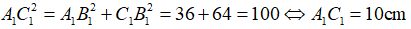
Nhận xét rằng:

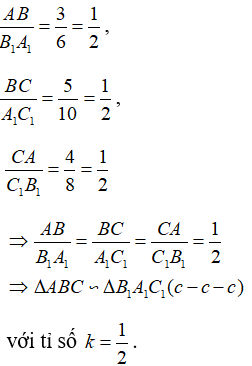
Câu 2: Cho ΔABC, điểm O ở bên trong tam giác. Gọi theo thứ tự là trung điểm của OA, OB, OC.

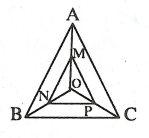a) Chứng minh rằng ΔABC đồng dạng với ΔMNP.

b) Tính chu vi của ΔMNP biết chu vi của ΔABC bằng 88cm.

Lời giải:

a) Trong ΔOAB, ta có :

M là trung điểm AO(gt)

N là trung điểm BO (gt)

⇒MN là đường trung bình ΔAOB

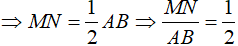
Trong ΔOAC, ta có :

M là trung điểm AO(gt)

P là trung điểm CO (gt)

⇒MP là đường trung bình ΔOAC

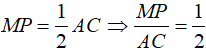
Trong ΔOBC, ta có :

N là trung điểm BO(gt)

P là trung điểm CO (gt)

⇒NP là đường trung bình ΔOBC

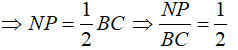
Vậy ta được:

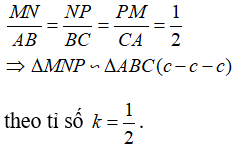
b) Ta có ngay:

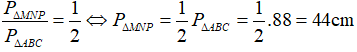
Câu 3: Cho 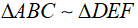theo tỉ số 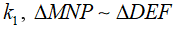theo tỉ số k₂. Chứng minh 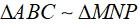theo tỉ số ?

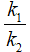Lời giải:

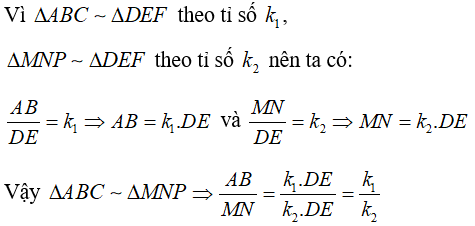
C. Bài tập tự luyện

Câu 1: Cho hai tam giác ABC và A'B'C' có kích thước như trong hình vẽ 35.

a.ΔABC và ΔA'B'C' có đồng dạng với nhau không? Vì sao?

b. Tính tỉ số chu vi của hai tam giác đó?

Câu 2: Cho ΔABC, biết AB = 6cm, BC = 10cm, CA = 8cm. Trên AB lấy điểm M sao cho AM = 4cm, trên AC lấy điểm N sao cho AN = 3cm. Chứng minh rằng ΔABC đồng dạng với ΔANM.

Câu 3: Cho ΔABC, lấy điểm M thuộc AB sao cho 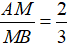. Kẻ hai đường thẳng qua M lần lượt song song với AC và BC cắt BC và AC lần lượt tại D và F.

a) Nêu tất cả các cặp tam giác đồng dạng.

b) Với mỗi cặp tam giác đồng dạng, hãy viết tỉ số đồng dạng tương ứng.

Câu 4: Cho ΔABC~ΔDEF, tỉ số đồng dạng bằng 2/3. Biết chu vi ΔABC là 24 cm. Tính chu vi ΔDEF

Câu 5: Cho ΔABC có AB = 3cm, BC = 5cm, CA = 7cm và ΔA'B'C' có A'B' = 4,5cm, B'C' = 7,5cm, C'A' = 10,5cm. Hỏi ΔABC và ΔA'B'C' có đồng dạng với nhau không? Tại sao?

Câu 6: Cho điểm M nằm trong ΔABC. Gọi G₁, G₂, G₃ lần lượt là trọng tâm các tam giác MBC, MCA, MAB. Chứng minh rằng .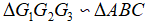

Câu 7: Cho ΔABC. Trên cạnh AB lấy các điểm I, K sao cho AI=IK=KB. Trên cạnh BC lấy các điểm E và D sao cho BD=DE=EC. Trên cạnh AC lấy điểm F và G sao cho AF=FG=GC. Gọi M là giao điểm của AD và BF, N là giao điểm của BG và CK, P là giao điểm của AE và CI. Chứng minh ΔABC~ΔNPM.

Câu 8: Cho tứ giác ABCD có AB = 2cm, BC = 10cm, CD = 12,5cm, AD = 4cm, BD = 5cm. Chứng minh rằng tứ giác ABCD là hình thang.