Các Bài toán thực tế về vận dụng định lí Pythagore lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Các Bài toán thực tế về vận dụng định lí Pythagore lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Các Bài toán thực tế về vận dụng định lí Pythagore.

Các Bài toán thực tế về vận dụng định lí Pythagore lớp 8 (bài tập + lời giải)

1. Phương pháp giải

Để giải các Bài toán thực tế về định lí Pythagore, ta thực hiện như sau:

Bước 1. Đưa các bài toán thực tế về tam giác vuông.

Bước 2. Áp dụng định lí Pythagore để tính cạnh của tam giác.

Bước 3. Kết luận độ dài khoảng cách cần tìm.

2. Ví dụ minh hoạ

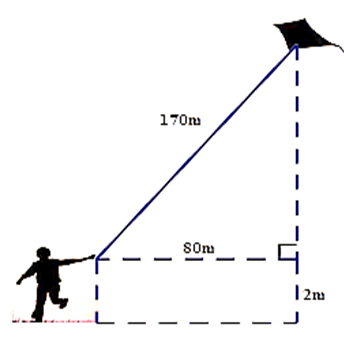
Ví dụ 1.Một bạn học sinh thả diều ngoài đồng, cho biết đoạn dây diều từ tay bạn đến diều dài 170 m và bạn đứng cách nơi diều được thả lên theo phương thẳng đứng là 80 m. Tính độ cao của con diều so với mặt đất, biết tay bạn học sinh cách mặt đất 2 m.

Hướng dẫn giải:

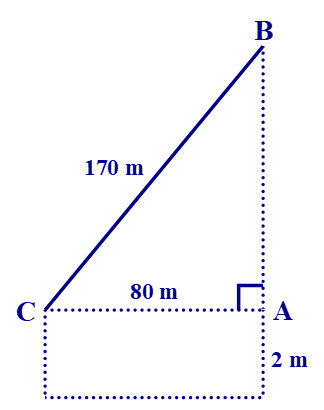
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore ta có:

AC² + AB² = BC²

Þ AB² = BC² – AC² = 170² – 80² = 22 500

Þ AB = 150 m.

Độ cao của con diều so với mặt đất là: 150 + 2 = 152 (m)

Vậy độ cao của con diều so với mặt đất là 152 m.

Ví dụ 2.Hai cây A và B được trồng dọc trên đường, cách nhau 24 m và cách đều cột đèn D. Ngôi trường C cách cột đèn D 9 m theo hướng vuông góc với đường. Tính khoảng cách từ mỗi cây đến ngôi trường.

Hướng dẫn giải:

Để tính khoảng cách từ mỗi cây đến trường, ta tính độ dài hai đoạn thẳng AC và BC.

*) Vì D cách đều A và B nên D là trung điểm của AB.

$DA=DB=\frac{AB}{2}=\frac{24}{2}=12\left(m\right)$.

*) Xét tam giác ADC vuông tại D, áp dụng định lí Pythagore ta có:

AC² = AD² + DC² = 12² + 9² = 225

$\Rightarrow$ AC = 15 m.

*) Xét tam giác ABC có CD là đường trung tuyến và CD vuông góc với AB tại D nên tam giác ABC cân tại C.

$\Rightarrow$ AB = AC = 15 m.

Vậy khoảng cách từ mỗi cây đến trường là 15 m.

3. Bài tập tự luyện

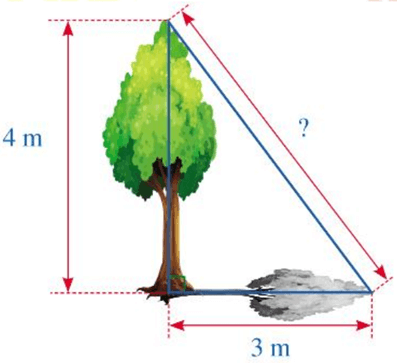
Bài 1. Hình dưới đây mô tả một cây cao 4 m. Biết rằng khi trời nắng, cây đổ bóng trên mặt đất, điểm xa nhất của bóng cây cách gốc cây một khoảng là 3 m.

Khoảng cách từ điểm xa nhất của bóng cây đến đỉnh của cây là:

A. 4 m;

B. 2 m;

C. 3 m;

D. 5 m.

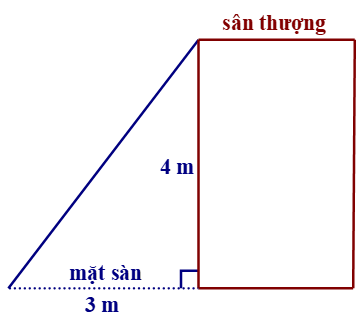
Bài 2. Bác thợ muốn xây một cầu thang bắc từ mặt sàn lên sân thượng. Biết rằng bức tường từ sàn lên sân thượng cao 4 m, chân cầu thang cách bức tường 3 m. Khi đó, chiều dài của cầu thang là:

A. 4 m;

B. 5 m;

C. 6 m;

D. 7 m.

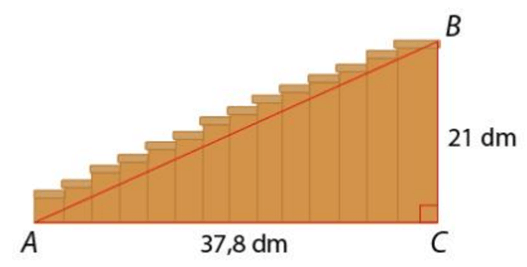
Bài 3. Một chiếc cầu thang có các kích thước như hình vẽ sau:

Tính độ dài đoạn thẳng AB.

A. AB » 43,2 dm;

B. AB » 43,3 dm;

C. AB » 44,2 dm;

D. AB » 44,3 dm.

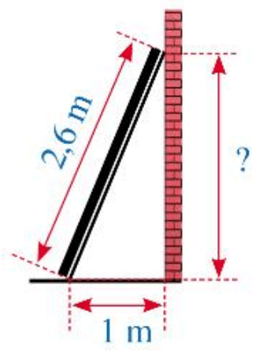
Bài 4. Hình dưới đây mô tả một thanh gỗ dài 2,6 m đặt dựa vào một bức tường thẳng đứng. Chân thanh gỗ cách mép tường một khoảng là 1 m. Khoảng cách từ điểm thanh gỗ chạm vào tường đến mặt đất là bao nhiêu mét?

A. 5,67 m;

B. 5,76 m;

C. 2,4 m;

D. 4,2 m.

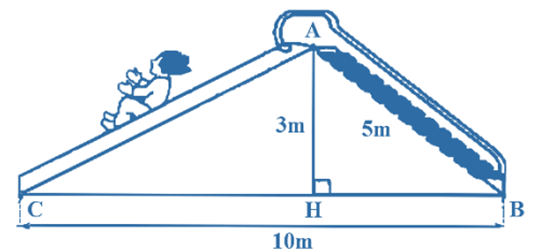
Bài 5. Cho hình vẽ:

Chiều dài đường trượt AC trong hình vẽ trên là:

A. 45 m;

B. $\sqrt{45}m$;

C. $\sqrt{27}m$;

D. 27 m.

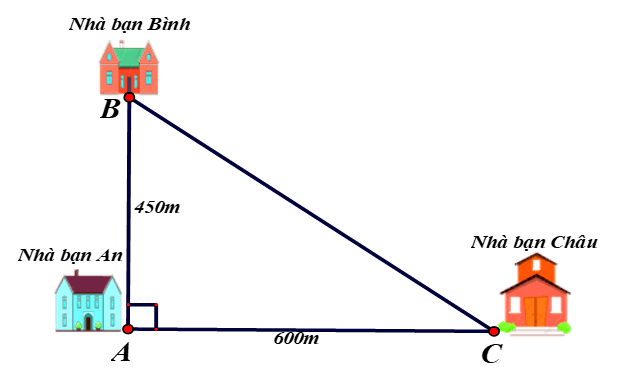
Bài 6. Nhà bạn An(vị trí A trên hình vẽ) cách nhà bạn Châu(vị trí C trên hình vẽ) 600 m và cách nhà bạn Bình (vị trí B trên hình vẽ)450 m. Biết rằng 3 vị trí: nhà An, nhà Bình và nhà Châu là 3 đỉnh của một tam giác vuông (xem hình vẽ). Hãy tính khoảng cách từ nhà Bình đến nhà Châu.

A. 300 m;

B. 450 m;

C. 600 m;

D. 750 m.

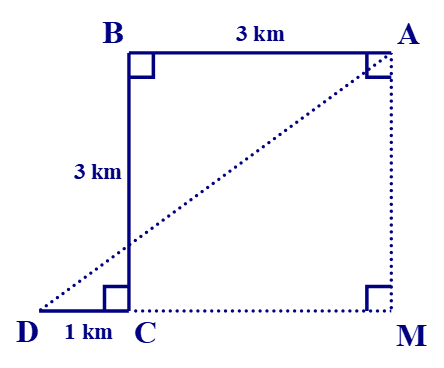
Bài 7. Để đón được một người khách, một xe taxi xuất phát từ vị trí điểm A, chạy dọc một con phố dài 3 km đến điểm B thì rẽ vuông góc sang trái, chạy được 3 km đến điểm C thì tài xế cho xe rẽ vuông góc sang phải, chạy 1 km nữa thì gặp người khách tại điểm D. Hỏi lúc đầu, khoảng cách từ chỗ người lái xe đến người khách là bao nhiêu ki-lô-mét?

A. 5 km;

B. 5 m;

C. 3 km;

D. 3 m.

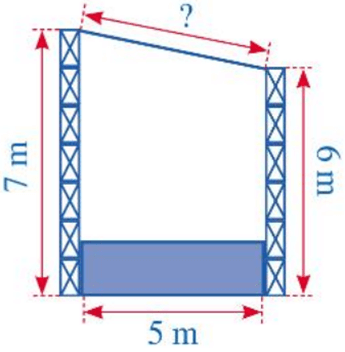
Bài 8. Cho hình vẽ:

Hình vẽ trên mô tả mặt cắt đứng của một sân khấu ngoài trời có mái che. Chiều cao của khung phía trước khoảng 7 m, chiều cao của khung phía sau là 6 m, hai khung cách nhau một khoảng 5 m. Chiều dài của mái che sân khấu khoảng … mét.

Số thích hợp để điền vào chỗ chấm là:

A. 5,0;

B. 5,1;

C. 5,2;

D. 5,3.

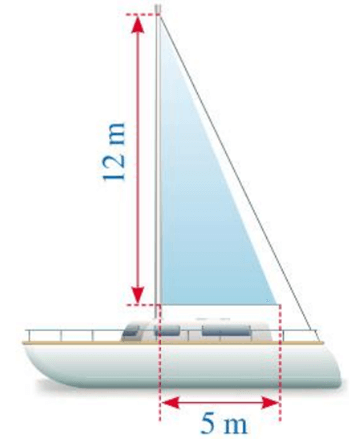
Bài 9. Hình dưới đây mô tả một cánh buồm có dạng tam giác vuông, được buộc vào cột buồm thẳng đứng, với độ dài hai cạnh góc vuông là 12 m và 5 m.

Chu vi của cánh buồm là:

A. 13 m;

B. 15 m;

C. 40 m;

D. 30 m.

Bài 10. Cho hình vẽ:

Hình vẽ trên mô tả mặt cắt dọc phần nổi trên mặt nước của một chiếc tàu thuỷ. Tính chu vi mặt cắt dọc phần nổi trên mặt nước của chiếc tàu thuỷ đó (làm tròn kết quả đến hàng phần mười).

A. 101,4 m;

B. 102,4 m;

C. 102,3 m;

D. 102,5 m.