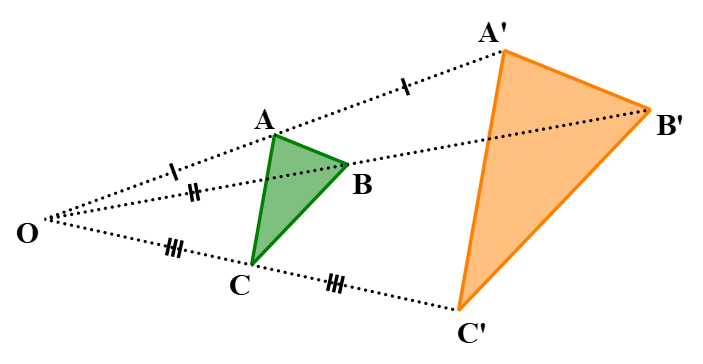Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh.

Nhận biết hai hình đồng dạng, hai hình đồng dạng phối cảnh lớp 8 (bài tập + lời giải)

1. Phương pháp giải

a) Hình đồng dạng phối cảnh

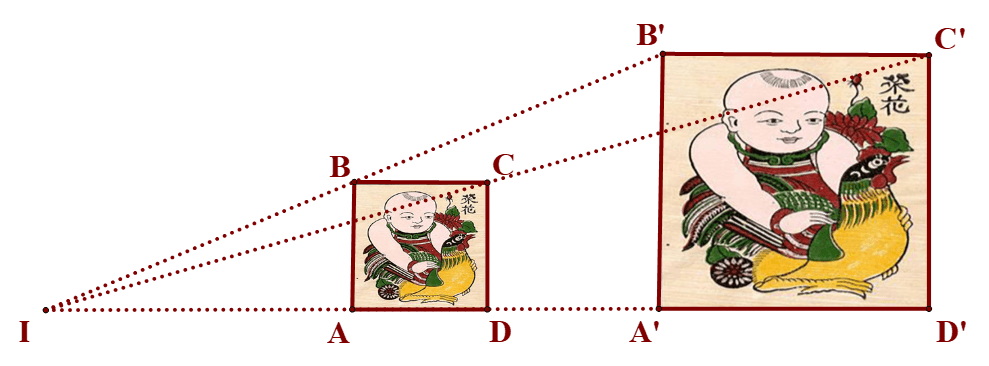
Hình 1

Quan sát Hình 1, ta thấy: Từ điểm O, “phóng to” hai lần tam giác ABC, ta sẽ nhận được tam giác A'B'C'. Tam giác A'B'C' gọi là đồng dạng phối cảnh (hay vị tự) với tam giác ABC, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số $k=\frac{A\text{'}B\text{'}}{AB}=2$ gọi là tỉ số vị tự.

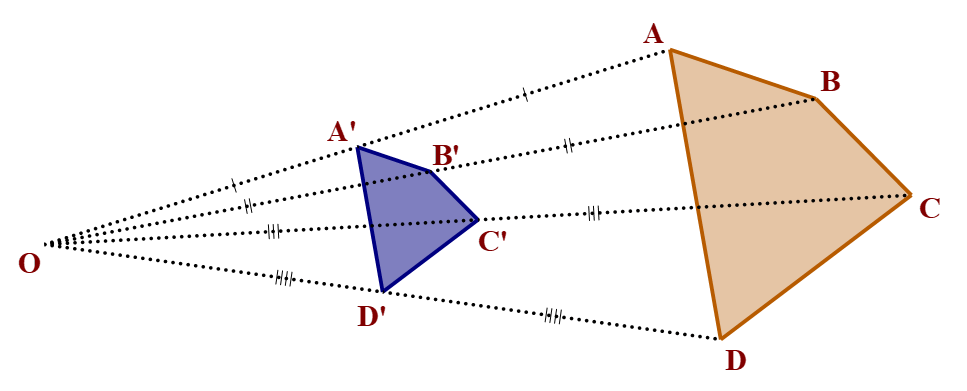
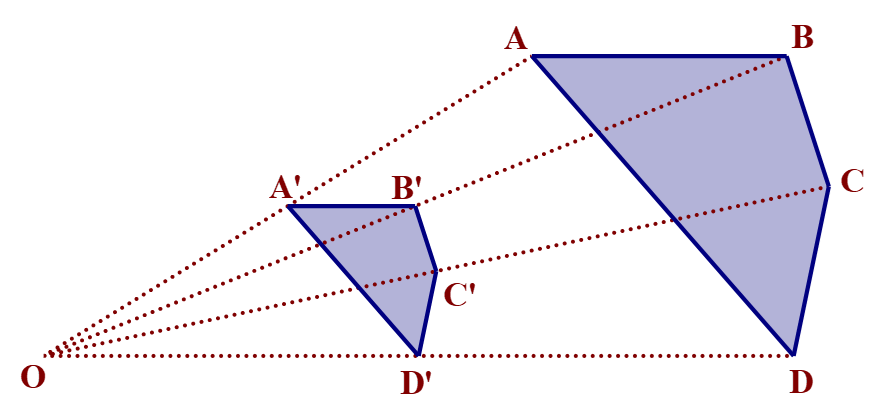
Hình 2

Quan sát hình 2, ta thấy: Từ điểm O, “thu nhỏ” hai lần tứ giác ABCD, ta sẽ nhận được tứ giác A'B'C'D'. Tứ giác A'B'C'D' gọi là đồng dạng phối cảnh (hay vị tự) với tứ giác ABCD, điểm O gọi là tâm đồng dạng phối cảnh, tỉ số $k=\frac{A\text{'}B\text{'}}{AB}=\frac{1}{2}$ gọi là tỉ số vị tự.

Tổng quát:

*) Cho H' là hình đồng dạng phối cảnh của H (tâm O) theo tỉ số k.

+ Khi k > 1, H' là hình “phóng to” của hình H theo tỉ số k.

+ Khi 0 < k < 1, H' là hình “thu nhỏ” của hình H theo tỉ số k.

*) Hình đồng dạng phối cảnh tỉ số k của đoạn thẳng AB là một đoạn thẳng A'B' (nằm trên đường thẳng song song hoặc trùng với đường thẳng AB) và A'B' = k.AB.

b) Hai hình đồng dạng

- Nếu có thể đặt hình H chồng khít lên hình H' thì ta nói hai hình H và H' là bằng nhau (hay còn gọi là hình H bằng hình H').

- Hình H' đồng dạng với hình H nếu hình H' bằng một hình nào đó đồng dạng phối cảnh với hình H.

c) Phương pháp giải

*) Để nhận dạng hai hình đồng dạng phối cảnh, ta thực hiện như sau:

Bước 1: Xác định các cặp đường thẳng cùng đi qua một điểm.

Bước 2: Xét tỉ số các cặp đoạn thẳng tương ứng xem bằng nhau hay không bằng nhau.

Bước 3: Kết luận các cặp hình đồng dạng phối cảnh.

*) Để chứng minh Hình H' đồng dạng với hình H, ta chứng minh hình H' bằng một hình nào đó đồng dạng phối cảnh với hình H.

2. Ví dụ minh hoạ

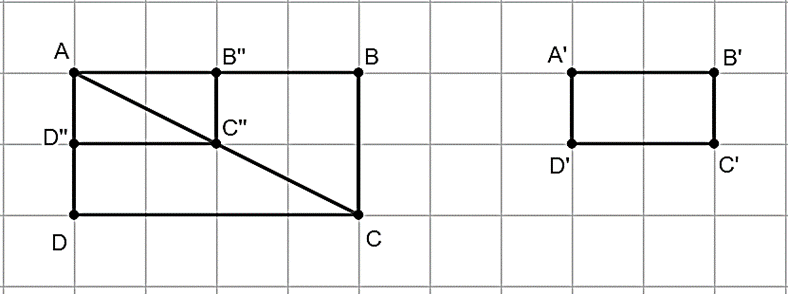
Ví dụ 1. Cho hình vẽ:

Biết các điểm A, B, C, D lần lượt là trung điểm của các đoạn thẳng OA', OB', OC', OD'. Cho biết hai hình chữ nhật ABCD và A'B'C'D' có đồng dạng phối cảnh hay không? Nếu có, hãy chỉ ra tâm đồng dạng phối cảnh.

Hướng dẫn giải:

Quan sát hình vẽ, ta thấy:

+) Bốn đường thẳng AA', BB', CC', DD' cùng đi qua điểm O;

+) Vì A, B, C, D lần lượt là trung điểm của các đoạn thẳng OA', OB', OC', OD' nên ta có $\frac{OA\text{'}}{OA}=\frac{OB\text{'}}{OB}=\frac{OC\text{'}}{OC}=\frac{OD\text{'}}{OD}$;

$\Rightarrow$ Hình chữ nhật A'B'C'D' và hình chữ nhật ABCD là đồng dạng phối cảnh và điểm O là tâm đồng dạng phối cảnh.

Ví dụ 2. Cho hai hình chữ nhật A'B'C'D' và ABCD sao cho $\frac{A\text{'}B\text{'}}{AB}=\frac{B\text{'}C\text{'}}{BC}$ . Hỏi hai hình chữ nhật A'B'C'D' và ABCD có đồng dạng hay không? Vì sao?

Hướng dẫn giải:

Trên tia AD ta lấy điểm D'' sao cho AD'' = A'D'. Qua D'' kẻ đường thẳng song song với DC, cắt tia AC tại C''. Qua C'' kẻ đường thẳng song song với BC, cắt tia AB tại B''.

Ta thấy tứ giác AB''C''D'' là hình chữ nhật và hình chữ nhật AB''C''D'' đồng dạng phối cảnh với hình chữ nhật ABCD. (1)

Áp dụng định lí Thalès trong tam giác ACD với C''D'' // CD, ta có:

$\frac{AC"}{AC}=\frac{AD"}{AD}$.

Do đó, $\frac{AB"}{AB}=\frac{AD"}{\text{AD}}=\frac{A\text{'}D\text{'}}{AD}=\frac{B\text{'}C\text{'}}{BC}=\frac{A\text{'}B\text{'}}{AB}$.

Suy ra, AB'' = A'B'.

Vì AB'' = A'B' và AD'' = A'D' nên hình chữ nhật AB''C''D'' bằng hình chữ nhật A'B'C'D' (2).

Từ (1) và (2) suy ra hai hình chữ nhật A'B'C'D' và ABCD đồng dạng.

3. Bài tập tự luyện

Bài 1. Cho các khẳng định sau:

(I) Hai hình đồng dạng phối cảnh (hay vị tự) không là hai hình đồng dạng.

(II) Nếu điểm O là tâm đồng dạng phối cảnh của hai đoạn thẳng AB và A'B' đồng dạng phối cảnh thì AB // A'B'.

(III) Hình H' gọi là đồng dạng với hình H nếu hình H bằng một hình nào đó đồng dạng phối cảnh với hình H.

Có bao nhiêu khẳng định đúng trong các khẳng định trên?

A. 0;

B. 1;

C. 2;

D. 3.

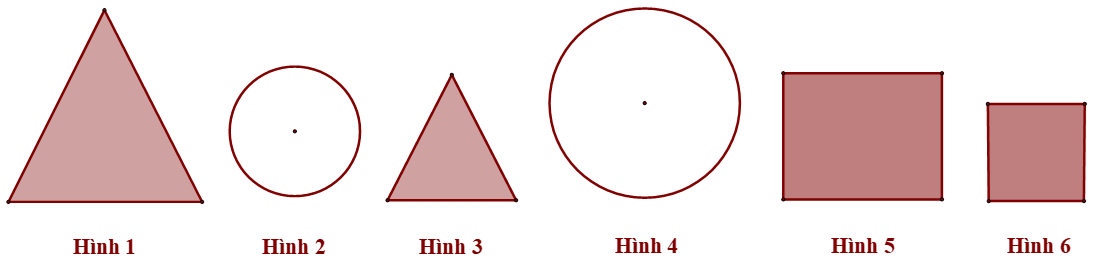
Bài 2. Cho các hình sau:

Có bao nhiêu cặp hình đồng dạng trong hình trên?

A. 1 cặp;

B. 2 cặp;

C. 3 cặp;

D. 4 cặp.

Bài 3. Phát biểu nào sau đây là đúng?

A. Hình H' gọi là đồng dạng với hình H nếu H' bằng H hoặc bằng một hình phóng to hay thu nhỏ của H;

B. Hình H' gọi là đồng dạng với hình H nếu H' lớn hơn H hoặc bằng một hình phóng to hay thu nhỏ của H;

C. Hình H' gọi là đồng dạng với hình H nếu H' bằng H hoặc lớn hơn một hình phóng to hay thu nhỏ của H;

D. Hình H' gọi là đồng dạng với hình H nếu H' nhỏ hơn H hoặc lớn hơn một hình phóng to hay thu nhỏ của H.

Bài 4. Cho hình vẽ:

Biết các điểm A, B, C, D lần lượt là trung điểm của các đoạn thẳng IA', IB', IC', ID'.

Khẳng định nào sau đây là sai?

A. Hai tứ giác ABCD và A'B'C'D' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh;

B. Hai đoạn thẳng AB và A'B' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh;

C. Hai đoạn thẳng BB' và AA' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh;

D. Hai đoạn thẳng BD và B'D' đồng dạng phối cảnh, điểm I là tâm đồng dạng phối cảnh.

Bài 5. Cho hai tứ giác A'B'C'D' và ABCD đồng dạng phối cảnh với nhau. O là tâm đồng dạng phối cảnh, tỉ số .

Biết AB = 3 cm; BC = 1,5 cm; CD = 2 cm; AD = 4 cm.

Chu vi tứ giác A'B'C'D' là:

A. 5 cm;

B. 5,25 cm;

C. 11 cm;

D. 10,5 cm.

Bài 6. Cho tam giác ABC có AB = 13 cm, BC = 14 cm, CA = 15 cm và D là một điểm phân biệt. Giả sử tam giác A'B'C' là hình đồng dạng phối cảnh của tam giác ABC với điểm D là tâm đồng dạng phối cảnh, tỉ số . Độ dài cạnh B'C' là:

A. 11,2 cm;

B. 10,4 cm;

C. 12 cm;

D. 14 cm.

Bài 7. Cho tam giác ABC có AB = 13, BC = 14, CA = 15 và E là một điểm phân biệt. Giả sử tam giác A''B''C'' là hình đồng dạng phối cảnh của tam giác ABC với điểm E là tâm đồng dạng phối cảnh, tỉ số . Chu vi của tam giác A''B''C'' là:

A. 42;

B. 43;

C. 33,5;

D. 33,6.

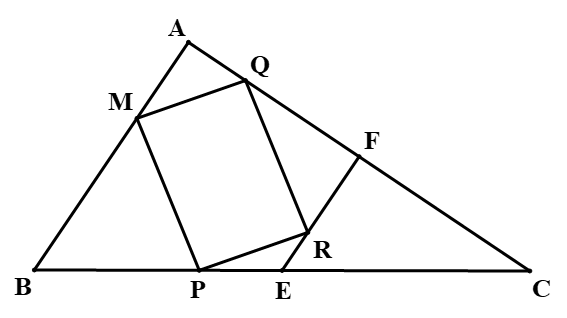
Bài 8. Cho tam giác ABC có E, F lần lượt là trung điểm của BC, AC. Các điểm M, P, R, Q lần lượt nằm trên AB, BE, EF, FA sao cho .

Cho các khẳng định sau:

(I) Hai đoạn thẳng FE và AB đồng dạng phối cảnh, điểm C là tâm đồng dạng phối cảnh.

(II) Hai đoạn thẳng MP và AE đồng dạng phối cảnh, điểm B là tâm đồng dạng phối cảnh và $\frac{BM}{BA}=\frac{BP}{BE}=\frac{3}{5}$.

(III) Hai đoạn thẳng PR và BF đồng dạng phối cảnh, điểm E là tâm đồng dạng phối cảnh.

Có bao nhiêu khẳng định đúng trong các khẳng định trên?

A. 0;

B. 1;

C. 2;

D. 3.

Bài 9. Cho tam giác ABC với trọng tâm O. Lấy điểm A', B', C' lần lượt là trung điểm của các đoạn thẳng OA, OB, OC. Khẳng định nào sau đây là đúng?

A. Hai tam giác A'B'C' và ABC đồng dạng phối cảnh và điểm O là tâm đồng dạng phối cảnh với tỉ số $\frac{2}{3}$;

B. Hai tam giác A'B'C' và ABC đồng dạng phối cảnh và điểm O là tâm đồng dạng phối cảnh với tỉ số $\frac{3}{2}$;

C. Hai tam giác A'B'C' và ABC đồng dạng phối cảnh và điểm O là tâm đồng dạng phối cảnh với tỉ số $\frac{1}{2}$;

D. Hai tam giác A'B'C' và ABC đồng dạng phối cảnh và điểm O là tâm đồng dạng phối cảnh với tỉ số $\frac{1}{3}$.

Bài 10. Cho điểm O nằm ngoài tam giác MNP. Trên các tia ON, OM, OP ta lần lượt lấy các điểm A, B, C sao cho $\frac{ON}{OA}=\frac{OM}{OB}=\frac{OP}{OC}=\frac{5}{3}$.

Khẳng định nào sau đây là đúng?

A. Tam giác MNP đồng dạng phối cảnh với tam giác ABC và điểm O là tâm đồng dạng phối cảnh;

B. Tam giác MPN đồng dạng phối cảnh với tam giác ABC và điểm O là tâm đồng dạng phối cảnh;

C. Tam giác ABC đồng dạng phối cảnh với tam giác NMP và điểm O là tâm đồng dạng phối cảnh;

D. Tam giác ABC đồng dạng phối cảnh với tam giác MNP và điểm O là tâm đồng dạng phối cảnh.