Các Bài toán thực tế về vận dụng các tam giác vuông đồng dạng lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Các Bài toán thực tế về vận dụng các tam giác vuông đồng dạng lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Các Bài toán thực tế về vận dụng các tam giác vuông đồng dạng.

Các Bài toán thực tế về vận dụng các tam giác vuông đồng dạng lớp 8 (bài tập + lời giải)

1. Phương pháp giải

Để giải các Bài toán thực tế về vận dụng các tam giác vuông đồng dạng ta thực hiện như sau:

Bước 1. Đưa các bài toán thực tế ghép vào tam giác vuông.

Bước 2. Chứng minh các cặp tam giác vuông đồng dạng.

Bước 3. Lập tỉ số, tính độ dài đoạn thẳng cần tìm.

Bước 4. Kết luận độ dài khoảng cách cần tìm.

2. Ví dụ minh hoạ

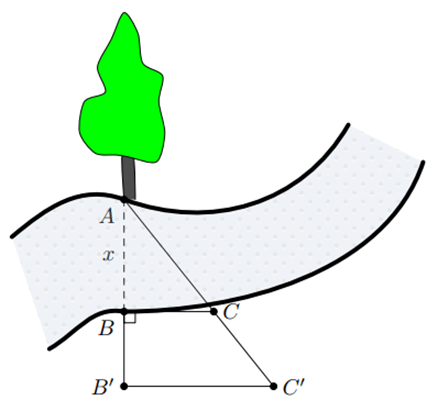
Ví dụ 1. Người ta tiến hành đo đạc các yếu tố cần thiết để tính chiều rộng của một khúc sông mà không cần phải sang bờ bên kia sông:

Biết BB' = 20 m, BC = 30 m và B'C' = 40 m. Tính độ rộng x của khúc sông.

Hướng dẫn giải:

Ta có AB' = AB + BB' = x + 20 (m).

Xét hai tam giác ABC và AB'C' có:

$\widehat{ABC}=\widehat{AB\text{'}C\text{'}}=90°$

Góc A chung.

Do đó, ∆ABC ᔕ ∆AB'C' (g.g).

Suy ra $\frac{AB}{AB\text{'}}=\frac{BC}{B\text{'}C\text{'}}$hay $\frac{x}{x+20}=\frac{30}{40}$. Suy ra 40x = 30(x + 20). Từ đó tìm được x = 60.

Vậy độ rộng của khúc sông là x = 60 m.

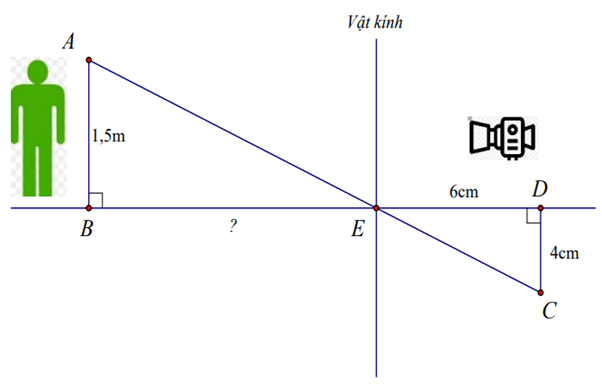
Ví dụ 2. Người ta dùng máy ảnh để chụp một người có chiều cao 1,5 m (như hình vẽ). Sau khi rửa phim thấy ảnh CD cao 4 cm. Biết khoảng cách từ phim đến vật kính của máy ảnh lúc chụp là ED = 6 cm. Hỏi người đó đứng cách vật kính máy ảnh một đoạn BE bao nhiêu xăng-ti-mét?

Hướng dẫn giải:

Đổi: 1,5 m = 150 cm

Xét tam giác ABE và tam giác CDE ta có:

$\widehat{ABE}=\widehat{CDE}=90°$

$\widehat{BEA}=\widehat{DEC}$ (2 góc đối đỉnh)

Do đó, ∆ABE ᔕ ∆CDE (g.g)

$\Rightarrow \frac{AB}{CD}=\frac{BE}{DE}$

$\Rightarrow BE=\frac{AB.DE}{CD}=\frac{150.6}{4}=225\left(cm\right)$.

Vậy người đó đứng cách vật kính máy ảnh một đoạn BE là 225 cm.

3. Bài tập tự luyện

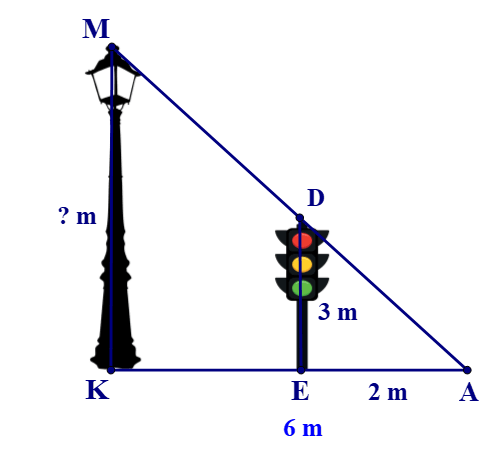
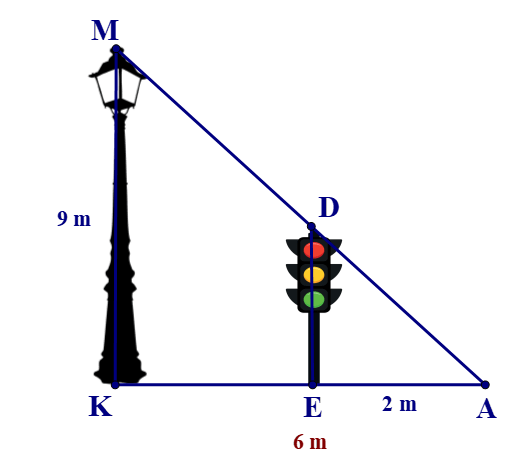
Bài 1. Bóng (AK) của một cột điện (MK) trên mặt đất dài 6 m. Cùng lúc đó một cột đèn giao thông (DE) cao 3 m có bóng (AE) dài 2 m. Tính chiều cao của cột điện (MK).

A. 3 m;

B. 6 m;

C. 9 m;

D. 12 m.

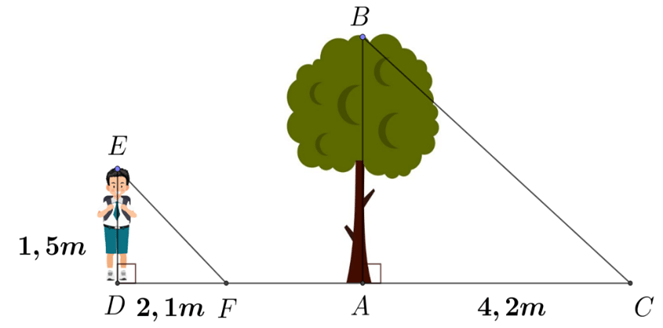
Bài 2. Một người cao 1,5 mét có bóng trên mặt đất dài 2,1 mét. Cùng lúc ấy, một cái cây gần đó có bóng trên mặt đất dài 4,2 mét.

Nhận xét nào sau đây là đúng?

A. Chiều cao của cái cây là 2 m;

B. Chiều cao của cái cây là 3,5 m;

C. Chiều cao của cái cây là 3 m;

D. Chiều cao của cái cây là 2,5 m.

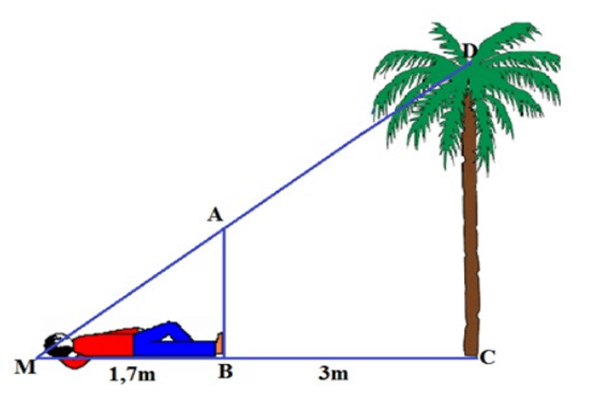
Bài 3. Bạn Hoàng muốn đo chiều cao của một cây dừa mọc thẳng đứng trong sân, bạn dùng một cây cọc AB dài 1,5 m và chiều dài thân mình để đo. Bạn nằm cách gốc cây 3 m (tính từ chân của bạn) và bạn cắm cọc thẳng đứng dưới chân mình thì bạn thấy đỉnh thân cọc và đỉnh cây thẳng hàng với nhau. Em hãy giúp bạn tính chiều cao của cây dừa, biết bạn Hoàng cao 1,7 m.

A. 4,0 m;

B. 4,1 m;

C. 4,2 m;

D. 4,3 m.

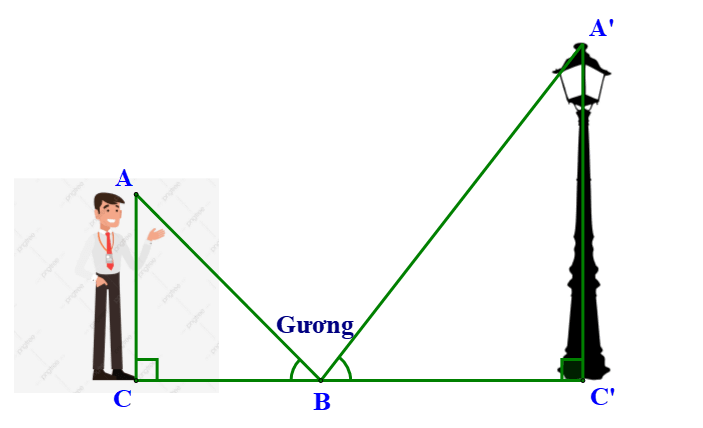
Bài 4. Để đo chiều cao của cột đèn ta làm như sau: Đặt tấm gương phẳng nằm trên mặt phẳng nằm ngang, mắt của người quan sát nhìn thẳng vào tấm gương, người quan sát di chuyển sao cho thấy được đỉnh ngọn đèn trong tấm gương và góc ABC bằng góc A'BC'. Cho chiều cao tính từ mắt của người quan sát đến mặt đất là AC = 1,6 m; khoảng cách từ gương đến chân người là BC = 0,8 m; khoảng cách từ gương đến chân cột đèn là BC' = 1,5 m. Tính chiều cao của cột đèn A'C'.

A. 2 m;

B. 2,5 m;

C. 3 m;

D. 3,5 m.

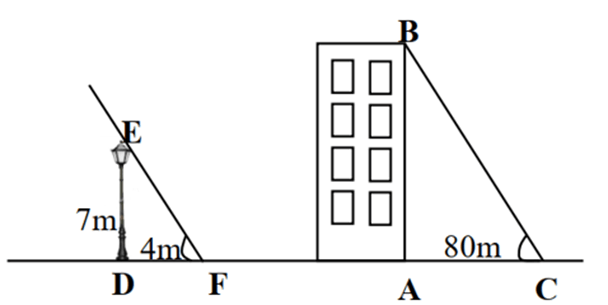
Bài 5. Một cột đèn cao 7 m có bóng trên mặt đất dài 4 m. Gần đấy có một toà nhà cao tầng có bóng trên mặt đất là 80 m (như hình vẽ). Em hãy cho biết toà nhà có bao nhiêu tầng, biết rằng mỗi tầng cao 3,5 m.

A. 40 tầng;

B. 45 tầng;

C. 30 tầng;

D. 20 tầng.

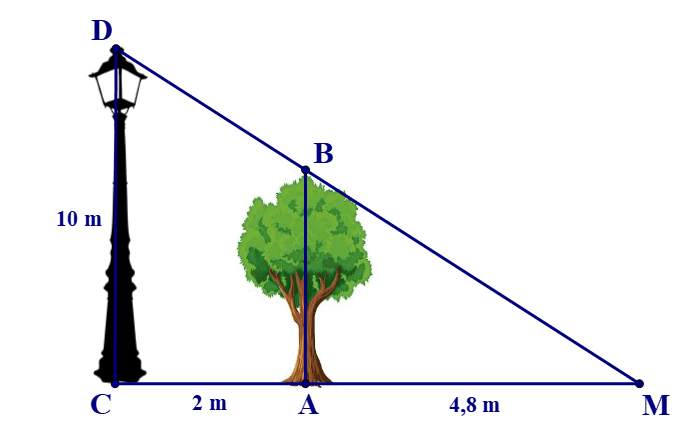
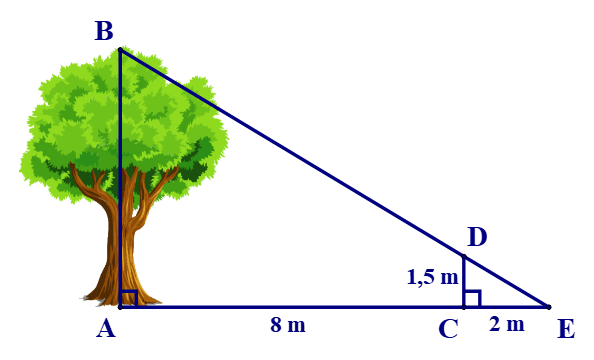
Bài 6. Một cột đèn cao 10 m chiếu sáng một cây xanh như hình bên dưới. Cây cách cột đèn 2 m và có bóng trải dài dưới mặt đất là 4,8 m. Tính chiều cao của cây xanh đó (làm tròn đến mét).

A. 5 m;

B. 6 m;

C. 7 m;

D. 8 m.

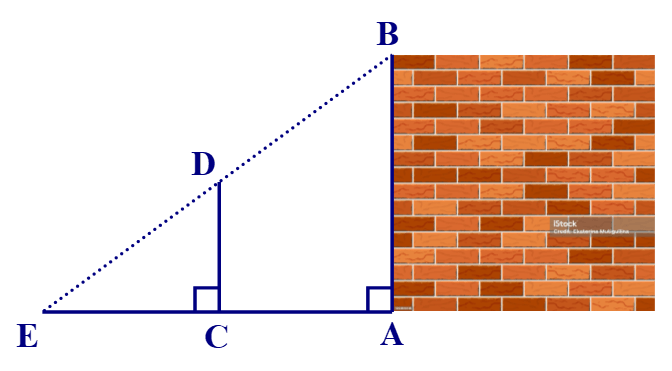
Bài 7. Một nhóm các bạn học sinh lớp 8 đã thực hành đo chiều cao AB của một bức tường như sau: Dùng một cái cọc CD đặt cố định vuông góc với mặt đất, với CD = 3 m và CA = 5 m. Sau đó, các bạn đã phối hợp để tìm được điểm E trên mặt đất là giao điểm của hai tia BD, AC và đo được CE = 2,5 m.

Tính chiều cao AB của bức tường.

A. 8 m;

B. 9 m;

C. 10 m;

D. 8,5 m.

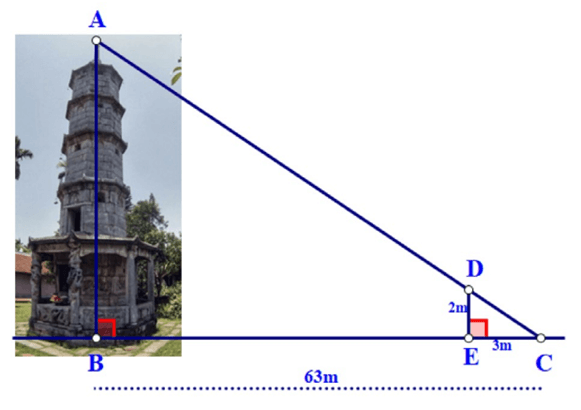
Bài 8. Bóng của một tháp trên mặt đất có độ dài BC = 63 m. Cùng thời điểm đó, một cây cột DE cao 2 m cắm vuông góc với mặt đất có bóng dài 3 m. Tính chiều cao của tháp.

A. 18 m;

B. 44 m;

C. 46 m;

D. 42 m.

Bài 9. Bóng (AK) của một cột điện (MK) cao 9 m trên mặt đất dài 6 m. Cùng lúc đó một cột đèn (DE) có bóng (AE) dài 2 m. Tính chiều cao của một đèn giao thông (DE).

A. 1 m;

B. 2 m;

C. 3 m;

D. 4 m.

Bài 10. Một người cắm một cái cọc vuông góc với mặt đất sao cho bóng của đỉnh cọc trùng với bóng của ngọn cây. Biết cọc cao 1,5 m so với mặt đất, chân cọc cách gốc cây 8 m và cách bóng của đỉnh cọc 2 m. Tính chiều cao của cây.

A. 7,5 m;

B. 15 m;

C. 30 m;

D. 12,5 m.