Chứng minh các tính chất hình học lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Chứng minh các tính chất hình học lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Chứng minh các tính chất hình học.

Chứng minh các tính chất hình học lớp 8 (bài tập + lời giải)

1. Phương pháp giải

Áp dụng định lí Pythagore chứng minh được:

+ Trong tam giác vuông cạnh huyền là cạnh lớn nhất.

+ So sánh độ dài các cạnh góc vuông, cạnh huyền tương ứng của nhiều tam giác vuông.

+ Đường thẳng vuông góc, sử dụng lí thuyết từ vuông góc đến song song, tính tổng các góc,…

2. Ví dụ minh hoạ

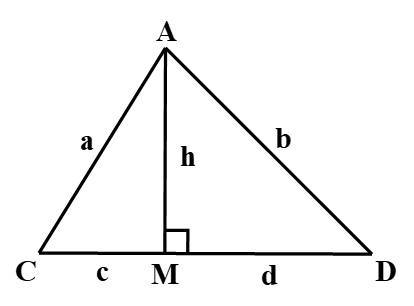
Ví dụ 1. Một chiếc cột có chiều cao h dựng thẳng đứng trên mặt đất tại điểm M, người ta kéo căng các sợi dây từ đỉnh cột (điểm A) lần lượt đến các điểm C và D trên mặt đất.

Biết rằng CM = c, DM = d và c < d. Hãy chứng minh rằng a < b.

Hướng dẫn giải:

Áp dụng định lí Pythagore cho hai tam giác vuông AMC và AMD, ta được:

AC² = AM² + CM² hay a² = h² + c²

AD² = AM² + DM² hay b² = h² + d²

Vì c < d nên c² < d² suy ra a² < b². Do đó, a < b.

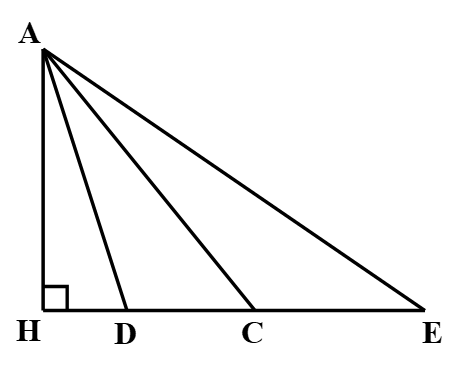
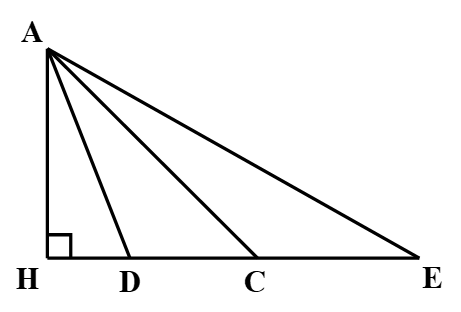
Ví dụ 2. Cho hình vẽ:

Trong các đoạn thẳng AC, AD, AE đoạn nào có độ dài lớn nhất, đoạn nào có độ dài nhỏ nhất?

Hướng dẫn giải:

Áp dụng định lí Pythagore cho ba tam giác vuông ADH, tam giác vuông ACH, tam giác vuông AEH ta được:

AD² = AH² + HD²

AC² = AH² + HC²

AE² = AH² + HE²

Quan sát hình vẽ, ta có: HD < HC < HE nên AD < AC < AE.

Vậy AE có độ dài lớn nhất, AD có độ dài nhỏ nhất.

3. Bài tập tự luyện

Bài 1. Nhận xét nào sau đây là đúng?

A. Trong tam giác vuông, cạnh huyền là cạnh lớn nhất;

B. Trong tam giác vuông, cạnh huyền là cạnh bé nhất;

C. Trong tam giác vuông, cạnh góc vuông bằng cạnh huyền;

D. Trong tam giác vuông, cạnh góc vuông lớn hơn cạnh huyền.

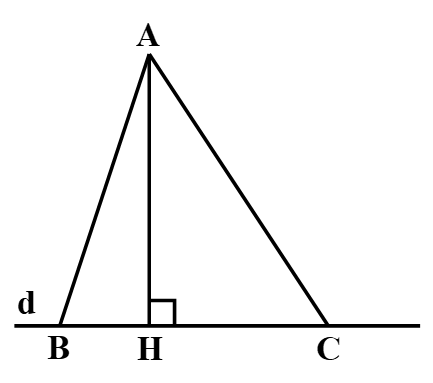
Bài 2. Cho hình vẽ:

Khẳng định nào sau đây là đúng?

A. HB > HC thì AB > AC;

B. HB > HC thì AB = AC;

C. HB < HC thì AB > AC;

D. HB = HC thì AB > AC.

Bài 3. Cho ba điểm A, B, C thẳng hàng và điểm B nằm giữa hai điểm A và C. Trên đường thẳng vuông góc với AC tại B ta lấy điểm H.

Khẳng định nào sau đây là đúng?

A. AH < BH;

B. AH < AB;

C. AH > BH;

D. AH = BH.

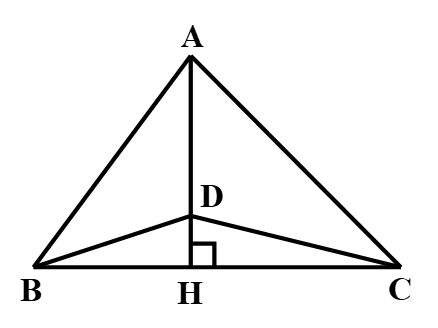
Bài 4. Cho hình vẽ sau:

Có AB < AC, khẳng định nào sau đây là đúng?

A. Nếu HB < HC thì BD > DC;

B. Nếu HB < HC thì BD < DC;

C. Nếu HB = HC thì BD < DC;

D. Nếu HB < HC thì BD = DC.

Bài 5. Cho điểm A không nằm trên d, kẻ $AH\perp d$tại H, B và C là các điểm tuỳ ý nằm trên d và khác H. Xét các khẳng định sau:

(I) AH < AB và AH < AC

(II) HB < HC

A. Chỉ có (I) đúng;

B. Chỉ có (II) đúng;

C. Cả (I) và (II) đều đúng;

D. Cả (I) và (II) đều sai.

Bài 6. Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM = 2 cm, tại M kẻ đường thẳng vuông góc với AB cắt AC tại H. Chọn khẳng định đúng.

A. BC vuông góc MH;

B. BC trùng với MH;

C. BC song song với MH;

D. Tất cả đều sai.

Bài 7. Cho tam giác ABC có độ dài các cạnh AB, BC, CA lần lượt là 4 cm, 3 cm, 5 cm. Trên tia đối của tia BA lấy điểm M sao cho BM = 2 cm, tại M kẻ đường thẳng vuông góc với AB cắt AC tại H.

Khẳng định nào sau đây là đúng?

A. $\widehat{CAB}+\widehat{CHM}=180°$;

B. $\widehat{ABM}+\widehat{CHM}=180°$;

C. $\widehat{BCH}+\widehat{CHM}=180°$;

D. $\widehat{CAB}+\widehat{BAH}=90°$.

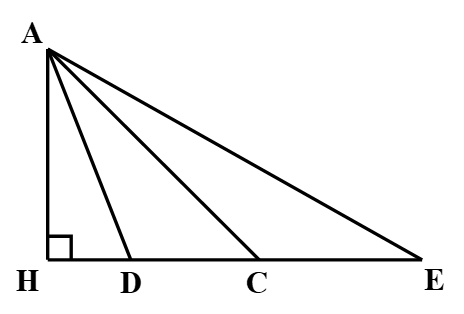
Bài 8. Cho hình vẽ:

Đoạn thẳng có độ dài ngắn nhất là:

A. AH;

B. AD;

C. AC;

D. AE.

Bài 9. Cho hình vẽ:

Nhận xét nào sau đây là đúng?

A. Vì HD < HC < HE nên AD > AC > AE;

B. Vì HD > HC > HE nên AD > AC > AE;

C. Vì HD < HC < HE nên AD < AC < AE;

D. Vì HD > HC > HE nên AD < AC < AE.

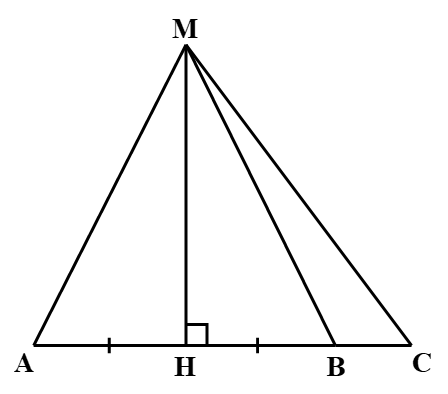
Bài 10. Cho hình vẽ sau:

Khẳng định nào sau đây là sai?

A. MA > MH;

B. HB < HC;

C. MA = MB;

D. MC < MA.