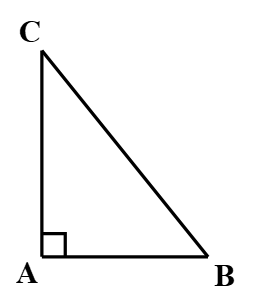Sử dụng định lí Pythagore chứng minh tam giác vuông lớp 8 (bài tập + lời giải)
Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Sử dụng định lí Pythagore chứng minh tam giác vuông lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Sử dụng định lí Pythagore chứng minh tam giác vuông.
Sử dụng định lí Pythagore chứng minh tam giác vuông lớp 8 (bài tập + lời giải)
1. Phương pháp giải
a) Định lí Pythagore
Trong một tam giác vuông, bình phương của cạnh huyền bằng tổng các bình phương của hai cạnh góc vuông.
b) Định lí Pythagore đảo
Nếu tam giác có bình phương của một cạnh bằng tổng các bình phương của hai cạnh kia thì tam giác đó là tam giác vuông.
vuông tại A.
→ Để chứng minh một tam giác khi biết độ dài ba cạnh là tam giác vuông, ta sử dụng định lí Pythagore đảo. Cụ thể kiểm tra bình phương của độ dài cạnh lớn nhất so với tổng các bình phương của hai cạnh còn lại.
2. Ví dụ minh hoạ
Ví dụ 1. Kiểm tra xem tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
a) 4 cm; 7 cm; 6 cm.
b) 6 cm; 8 cm; 10 cm.
Hướng dẫn giải:
a) Ta có:
42 + 62 = 52
72 = 49
Do đó, 42 + 62 ≠ 72.
Vậy tam giác có độ dài ba cạnh 4 cm, 7 cm, 6 cm không phải là tam giác vuông (định lí Pytagore đảo).
b) Ta có:
62 + 82 = 100
102 = 100
Do đó, 62 + 82 = 102.
Vậy tam giác có độ dài ba cạnh 6 cm, 8 cm, 10 cm không phải là tam giác vuông (định lí Pytagore đảo).
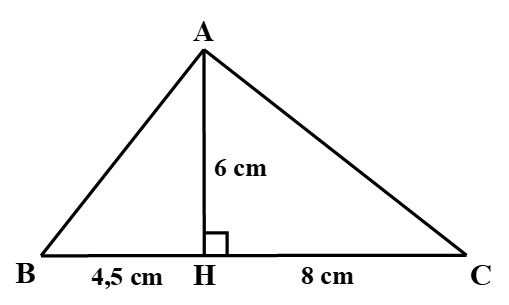
Ví dụ 2. Cho tam giác ABC, đường cao AH. Biết AH = 6 cm; BH = 4,5 cm; HC = 8 cm. Hỏi tam giác ABC là tam giác gì?
Hướng dẫn giải:
*) Xét tam giác ABH vuông tại H, áp dụng định lí Pythagore ta có:
*) Xét tam giác ACH vuông tại H, áp dụng định lí Pythagore ta có:
*) BC = BH + HC = 4,5 cm + 8 cm = 12,5 cm
Ta có:
vuông tại A (định lí Pythagore đảo).
3. Bài tập tự luyện
Bài 1. Tam giác nào là tam giác vuông trong các tam giác có độ dài ba cạnh như sau:
A. 11 cm; 7 cm; 8 cm;
B. 12 dm; 15 dm; 18 dm;
C. 9 m; 12 m; 15 m;
D. 6 m; 7 m; 9 m.
Bài 2. Cho tam giác ABC có độ dài ba cạnh AB = 6 cm, BC = 8 cm, AC = 10 cm. Khẳng định nào sau đây là đúng?
A. Tam giác ABC vuông tại A;
B. Tam giác ABC vuông tại B;
C. Tam giác ABC vuông tại C;
D. Không thể kết luận được.
Hướng dẫn giải:
Bài 3. Xét các khẳng định sau:
I) Tam giác có độ dài ba cạnh là 6 cm, 10 cm, 8 cm là tam giác vuông.
II) Tam giác có độ dài ba cạnh là 8 cm, 10 cm, 8 cm không phải là tam giác vuông.
Chọn câu trả lời đúng.
A. Chỉ có (I) đúng;
B. Chỉ có (II) đúng;
C. Cả (I) và (II) đều đúng;
D. Cả (I) và (II) đều sai.
Bài 4. Cho tam giác ABC, đường cao AH. Biết AC = 15 cm, AH = 12 cm, BH = 9 cm. Kết luận nào sau đây là đúng?
A. vuông;
B. cân;
C. tù;
D. vuông cân.
Bài 5. Cho các bộ ba số sau:
(a) 1 cm, 2 cm, 2 cm;
(b) 2 cm, 4 cm, 20 cm;
(c) 5 cm, 4 cm, 3 cm;
(d) 2 cm, 2 cm, .
Có bao nhiêu bộ ba số đo là độ dài ba cạnh của một tam giác vuông?
A. 0;
B. 1;
C. 2;
D. 3.
Bài 6. Cho tam giác ABC vuông tại A, có AB = 6 cm, AC = 8 cm. D là một điểm sao cho BD = 16 cm, CD = 24 cm. Khẳng định nào sau đây là đúng?
A. Ba điểm B, C, D thẳng hàng;
B. Tam giác BCD là tam giác vuông;
C. Tam giác BCD không thể là tam giác vuông;
D. Tam giác BCD là tam giác cân.
Bài 7. Cho tam giác DEF có , . Để tam giác DEF vuông tại D thì độ dài của cạnh DF là:
A. 7 cm;
B. ;
C. 15 cm;
D. .
Bài 8. Một khung gỗ ABCD được tạo thành từ 5 thanh nẹp có độ dài như sau:
AB = CD = 48 cm
BC = AD = 36 cm
AC = 60 cm
Kết luận nào sau đây là đúng?
A. Tứ giác ABCD là hình bình hành;
B. Tứ giác ABCD là hình thoi;
C. Tứ giác ABCD là hình chữ nhật;
D. Tứ giác ABCD là hình thang cân.
Bài 9. Một khung gỗ ABCD được tạo thành từ 5 thanh nẹp có độ dài như sau:
AB = CD = 48 cm
BC = AD = 36 cm
AC = 60 cm
Khẳng định nào sau đây là đúng?
A. ;
B. ;
C. ;
D. .
Bài 10. Cho tam giác ABH vuông tại H có AB = 20 cm, BH = 12 cm. Trên tia đối của tia HB lấy điểm C sao cho . Chọn đáp án đúng.
A. ;
B. ;
C. ;
D. .