Hai tam giác đồng dạng và tính chất của hai tam giác đồng dạng lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Hai tam giác đồng dạng và tính chất của hai tam giác đồng dạng lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Hai tam giác đồng dạng và tính chất của hai tam giác đồng dạng.

Hai tam giác đồng dạng và tính chất của hai tam giác đồng dạng lớp 8 (bài tập + lời giải)

1. Phương pháp giải

a) Định nghĩa

- Tam giác A'B'C' được gọi là đồng dạng với tam giác ABC nếu:

$\frac{\text{A'B'}}{\text{AB}}=\frac{\text{B'C'}}{\text{BC}}=\frac{\text{A'C'}}{\text{AC}};\widehat{\text{A'}}\text{=}\hat{\text{A}}\text{,}\widehat{\text{B'}}\text{=}\hat{\text{B}}\text{,}\widehat{\text{C'}}\text{=}\hat{\text{C}}$.

- Kí hiệu: ΔA'B'C' ᔕΔABC.

- Khi tam giác A'B'C' đồng dạng với tam giác ABC:

+ Ta viết ΔA'B'C' ᔕΔABC với các đỉnh được ghi theo thứ tự các góc bằng nhau.

+ Tỉ số các cạnh tương ứng $\frac{\text{A'B'}}{\text{AB}}=\frac{\text{B'C'}}{\text{BC}}=\frac{\text{A'C'}}{\text{AC}}=\text{k}$ gọi là tỉ số đồng dạng.

+ Nếu ΔA'B'C' = ΔABC thì ΔA'B'C' ᔕΔABC theo tỉ số đồng dạng là 1.

b) Tính chất

- Mỗi tam giác đồng dạng với chính nó.

- Nếu ΔA'B'C' ᔕΔABC với tỉ số đồng dạng k thì ΔABC ᔕΔA'B'C' với tỉ số đồng dạng $\frac{1}{k}$.

- Nếu ΔA"B"C" ᔕΔA'B'C' với tỉ số đồng dạng k và ΔA'B'C' ᔕΔABC với tỉ số đồng dạng m thì ΔA"B"C" ᔕΔABC với tỉ số đồng dạng k ∙ m.

2. Ví dụ minh họa

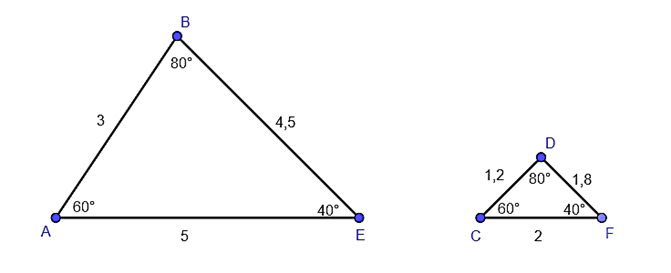
Ví dụ 1. Hai tam giác ở hình dưới đây có đồng dạng không? Vì sao?

Hướng dẫn giải:

Xét hai tam giác ABE và CDF có:

$\hat{\text{A}}\text{=}\hat{\text{C}}\text{= 60}°\text{,}\hat{\text{B}}\text{=}\hat{\text{D}}\text{= 80}°\text{,}\hat{\text{E}}\text{=}\hat{\text{F}}\text{= 40}°\text{;}$

$\frac{\text{BA}}{\text{DC}}=\frac{\text{BE}}{\text{DF}}=\frac{\text{AE}}{\text{CF}}=\frac{5}{2}$

Vậy theo định nghĩa hai tam giác đồng dạng ta có ΔABE ᔕΔCDF.

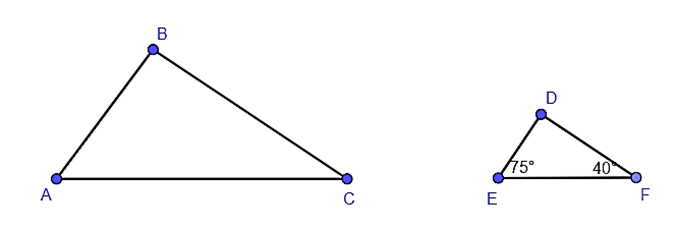
Ví dụ 2. Cho ΔABC ᔕΔEDF (hình bên dưới), biết . Tính số đo góc B.

Hướng dẫn giải:

Trong tam giác DEF có:

$\hat{\text{D}}\text{+}\hat{\text{E}}\text{+}\hat{\text{F}}=180°$ (định lí tổng 3 góc trong một tam giác).

Suy ra $\hat{\text{D}}=180°-\hat{\text{E}}-\hat{\text{F}}=180°-75°-40°=65°$.

Vì ΔABC ᔕΔEDF nên .

3. Bài tập tự luyện

Bài 1. Cho ΔMNQ ᔕΔABC, khẳng định nào sau đây là đúng?

A. ΔNMQ ᔕΔCAB;

B. ΔQMN ᔕΔCAB;

C. ΔQNM ᔕΔBAC;

D. ΔNQM ᔕΔBAC.

Bài 2. Khẳng định nào sau đây là sai?

A. Hai tam giác bằng nhau thì đồng dạng với nhau;

B. Mỗi tam giác đồng dạng với chính nó;

C. Hai tam giác đồng dạng thì bằng nhau;

D. Hai tam giác gọi là đồng dạng với nhau nếu chúng có các cặp góc tương ứng bằng nhau và các cặp cạnh tương ứng tỉ lệ.

Bài 3. ΔMNQ đồng dạng với ΔOHK khi nào?

A. $\frac{\text{MN}}{\text{OH}}=\frac{\text{NQ}}{\text{HK}}=\frac{\text{MQ}}{\text{OK}}\text{và}\hat{\text{M}}\text{=}\hat{\text{O}}\text{,}\hat{\text{N}}\text{=}\hat{\text{H}}\text{,}\hat{\text{Q}}\text{=}\hat{\text{K}}$;

B. MN // OH;

C. $\frac{\text{MN}}{\text{OH}}=\frac{\text{NQ}}{\text{OK}}=\frac{\text{MQ}}{\text{HK}}$;

D. $\hat{\text{M}}\text{=}\hat{H}\text{,}\hat{\text{N}}\text{=}\hat{O}\text{,}\hat{\text{Q}}\text{=}\hat{\text{K}}$.

Bài 4. ΔABC ᔕΔDEF với tỉ số đồng dạng là $\frac{3}{2}$. Khi đó ΔDEF ᔕΔABC theo tỉ số đồng dạng k bằng bao nhiêu?

A. $\frac{3}{2}$;

B. 3;

C. 2;

D. $\frac{2}{3}$.

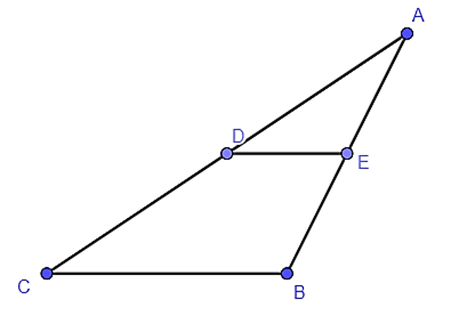
Bài 5. Cho tam giác ABC, DE là đường trung bình của tam giác (hình bên dưới). Khi đó ΔAED ᔕΔABC theo tỉ số đồng dạng k bằng:

A. $\frac{1}{2}$;

B. 2;

C. 1;

D. 0.

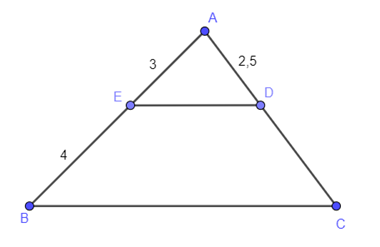
Bài 6. Cho ΔABC ᔕΔAED với số đo các cạnh như hình vẽ. Độ dài cạnh AC là

A. $\frac{15}{8}$;

B. $\frac{10}{3}$;

C. $\frac{35}{6}$;

D. $\frac{24}{5}$.

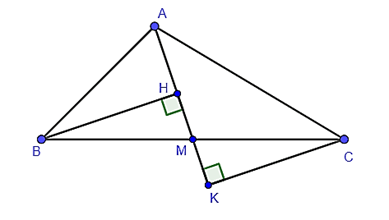
Bài 7. Cho tam giác ABC có AM là đường trung tuyến. Kẻ BH và CK lần lượt vuông góc với AM (hình bên dưới). Khi đó tam giác MBH đồng dạng với tam giác nào dưới đây?

A. Tam giác AHB;

B. Tam giác HMC;

C. Tam giác AKC;

D. Tam giác MCK.

Bài 8. Cho ΔABC ᔕΔMNQ với tỉ số đồng dạng k = 3, biết AC = 12 cm. Độ dài cạnh QM bằng:

A. 12 cm;

B. 4 cm;

C. 36 cm;

D. 6 cm.

Bài 9. Cho ΔABC ᔕΔDEF với tỉ số đồng dạng k₁ = 2, ΔDEF ᔕΔMNQ với tỉ số đồng dạng k₂ = 3. Khẳng định nào sau đây là đúng?

A. ΔMNQ ᔕΔABC với tỉ số đồng dạng k = 6;

B. ΔABC ᔕΔMNQ với tỉ số đồng dạng k = $\frac{3}{2}$;

C. ΔABC ᔕΔMNQ với tỉ số đồng dạng k = 6;

D. ΔABC ᔕΔMNQ với tỉ số đồng dạng k = $\frac{2}{3}$.

Bài 10. Cho ΔABC ᔕΔADE với tỉ số đồng dạng k, biết DE = 4, BC = 12. Tỉ số đồng dạng k bằng

A. 3;

B. $\frac{1}{3}$;

C. 2;

D. 6.