Trường hợp đồng dạng đặc biệt của hai tam giác lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Trường hợp đồng dạng đặc biệt của hai tam giác lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Trường hợp đồng dạng đặc biệt của hai tam giác.

Trường hợp đồng dạng đặc biệt của hai tam giác lớp 8 (bài tập + lời giải)

1. Phương pháp giải

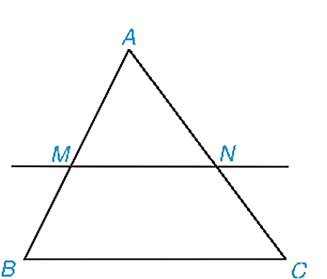
Sử dụng định lí: Nếu một đường thẳng cắt hai cạnh (hoặc phần kéo dài của hai cạnh) của một tam giác và song song với cạnh thứ ba thì nó tạo thành một tam giác mới đồng dạng với tam giác đã cho.

Trong hình vẽ trên: ∆ABC có MN // BC, M ∈ AB, N ∈ AC, khi đó ∆AMN ᔕ∆ABC.

2. Ví dụ minh họa

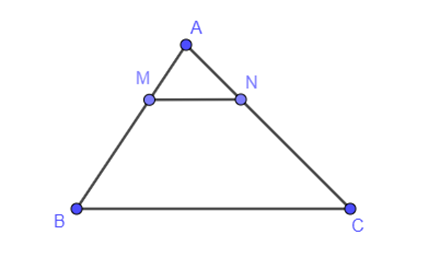
Ví dụ 1. Cho tam giác ABC, lấy hai điểm M và N lần lượt trên các cạnh AB, AC sao cho MN // BC. Viết tên các cặp góc bằng nhau.

Hướng dẫn giải:

Xét tam giác ABC, do MN // BC nên ΔAMN ᔕΔABC.

Suy ra $\widehat{\text{AMN}}\text{=}\widehat{\text{ABC}},\widehat{\text{ANM}}\text{=}\widehat{\text{ACB}}$.

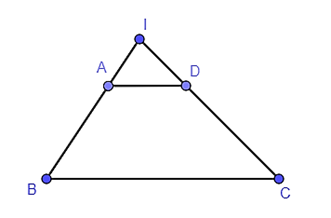
Ví dụ 2. Cho hình thang ABCD (AD // BC). Gọi I là giao điểm của AB và DC. Chứng minh ΔIAD ᔕΔIBC.

Hướng dẫn giải:

Xét tam giác IBC, do AD // BC nên ΔIAD ᔕΔIBC.

3. Bài tập tự luyện

Bài 1. Cho tam giác ABC có M, N, P lần lượt là trung điểm các cạnh AB, AC, BC. Trong hình vẽ được có bao nhiêu cặp tam giác đồng dạng?

A. 4;

B. 6;

C. 8;

D. 10.

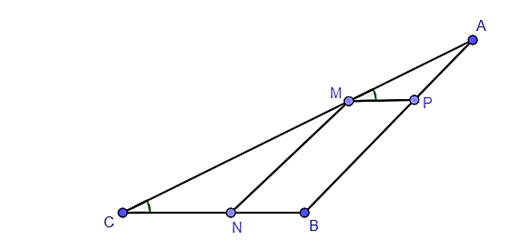
Bài 2. Cho hình vẽ sau biết MN // AB. Khẳng định nào sau đây là sai?

A. ΔAMP ᔕΔACB;

B. ΔMCN ᔕΔACB;

C. ΔAMP ᔕΔMCN;

D. Cả A, B, C đều sai.

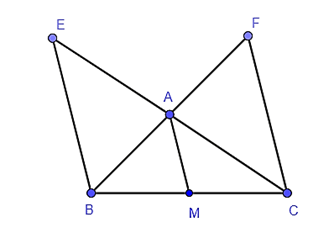
Bài 3. Cho hình vẽ, biết BE // AM // CF. Khi đó $\frac{\text{1}}{\text{BE}}+\frac{\text{1}}{\text{CF}}$ bằng

A. $\frac{\text{1}}{\text{AM}}$;

B. $\frac{\text{1}}{\text{BC}}$;

C. $\frac{2}{\text{AM}}$;

D. $\frac{2}{\text{BC}}$.

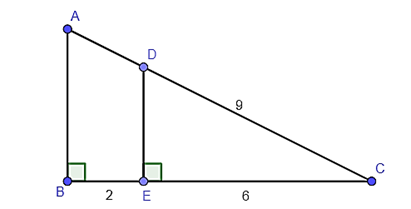
Bài 4. Cho hình dưới đây, khi đó độ dài cạnh AC là

A. 3;

B. $\frac{4}{3}$;

C. 12;

D. $\frac{16}{3}$.

Bài 5. Cho tam giác ABC và các điểm M, N lần lượt trên các cạnh AB, AC sao cho MN // BC. Khẳng định nào sau đây là đúng?

A. $\frac{\text{AM}}{\text{AB}}=\frac{\text{AN}}{\text{AC}}=\frac{\text{MN}}{\text{BC}}$;

B. $\frac{\text{AM}}{\text{AB}}=\frac{\text{AC}}{\text{AN}}=\frac{\text{MN}}{\text{BC}}$;

C. $\frac{\text{AB}}{\text{AM}}=\frac{\text{AC}}{\text{AN}}=\frac{\text{MN}}{\text{BC}}$;

D. $\frac{\text{AM}}{\text{AB}}=\frac{\text{AN}}{\text{AC}}=\frac{\text{BC}}{\text{MN}}$.

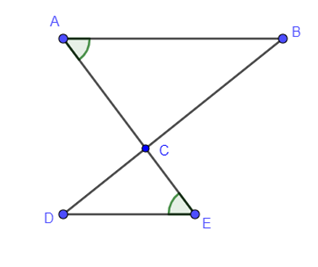
Bài 6. Cho hình sau, hãy chỉ ra hai tam giác đồng dạng và tỉ số đồng dạng của hai tam giác đó.

A. ΔCAB ᔕΔCDE với tỉ số đồng dạng $\text{k}=\frac{\text{CA}}{\text{CD}}$;

B. ΔABC ᔕΔDEC với tỉ số đồng dạng $\text{k}=\frac{\text{AB}}{\text{DE}}$;

C. ΔDEC ᔕΔBAC với tỉ số đồng dạng $\text{k}=\frac{\text{BC}}{\text{DC}}$;

D. ΔDEC ᔕΔBAC với tỉ số đồng dạng $\text{k}=\frac{\text{DE}}{\text{BA}}$.

Bài 7. Cho hình bình hành ABCD. Lấy E trên cạnh BC, tia DE cắt AB tại F. Khi đó tam giác FBE đồng dạng với tam giác nào dưới đây?

A. Tam giác FAD;

B. Tam giác DCE;

C. Cả A, B đều sai;

D. Cả A, B đều đúng.

Bài 8. Nếu tam giác MNQ có HK // MN (H ∈ NQ, K ∈ MQ) thì

A. ΔKQH ᔕΔNQM;

B. ΔKQH ᔕΔMQN;

C. ΔMNQ ᔕΔHKQ;

D. ΔMNQ ᔕΔQKH.

Bài 9. Cho tứ giác MNPQ. Đường chéo NQ chia tứ giác thành hai tam giác đồng dạng với nhau là ΔMNQ và ΔNQP. Khẳng định nào sau đây là đúng?

A. MNPQ là hình chữ nhật;

B. MNPQ là hình bình hành;

C. MNPQ là hình thang;

D. MNPQ là hình vuông.

Bài 10. Cho tam giác ABC, DE // BC (D ∈ AB, E ∈ AC). Biết AB = 5 cm, BC = 9 cm, AD = 2 cm, độ dài của ED là:

A. 3,6 cm;

B. 22,5 cm;

C. 1,1 cm;

D. 5,5 cm.