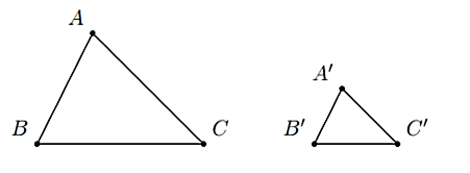Trường hợp đồng dạng thứ nhất của tam giác lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Trường hợp đồng dạng thứ nhất của tam giác lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Trường hợp đồng dạng thứ nhất của tam giác.

Trường hợp đồng dạng thứ nhất của tam giác lớp 8 (bài tập + lời giải)

1. Phương pháp giải

- Trường hợp đồng dạng thứ nhất của tam giác (cạnh – cạnh – cạnh):

Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.

∆ABC và ∆A'B'C' có $\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{A\text{'}C\text{'}}=\frac{BC}{B\text{'}C\text{'}}$ thì ∆ABC ᔕ ∆A'B'C'.

→ Để chứng minh hai tam giác đồng dạng khi biết độ dài các cạnh của nó, ta lập các tỉ số giữa các cạnh tương ứng của hai tam giác và chứng minh chúng bằng nhau.

- Áp dụng trường hợp đồng dạng thứ nhất vào tam giác vuông:

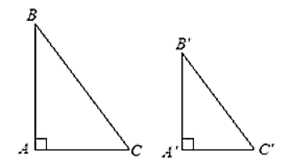
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

∆ABC và ∆A'B'C' có $\hat{A}=\widehat{A\text{'}}=90°$ và $\frac{AB}{A\text{'}B\text{'}}=\frac{BC}{B\text{'}C\text{'}}$ thì ∆ABC ᔕ ∆A'B'C'.

2. Ví dụ minh họa

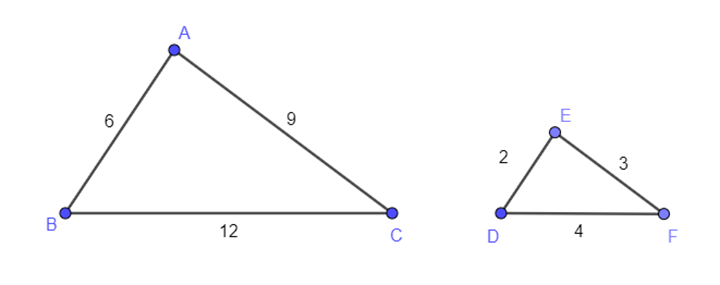
Ví dụ 1. Cho hai tam giác ABC và EDF như hình vẽ. Tam giác ABC, EDF có đồng dạng với nhau không? Vì sao?

Hướng dẫn giải:

Ta có $\frac{\text{AB}}{\text{DE}}=\frac{6}{2}=3,\frac{\text{AC}}{\text{EF}}=\frac{9}{3}=3,\frac{\text{BC}}{\text{DF}}=\frac{12}{4}=3$.

Suy ra $\frac{\text{AB}}{\text{DE}}=\frac{\text{AC}}{\text{EF}}=\frac{\text{BC}}{\text{DF}}$.

Xét hai tam giác ABC và EDF có: $\frac{\text{AB}}{\text{DE}}=\frac{\text{AC}}{\text{EF}}=\frac{\text{BC}}{\text{DF}}$.

Suy ra ΔABC ᔕΔEDF (c – c – c).

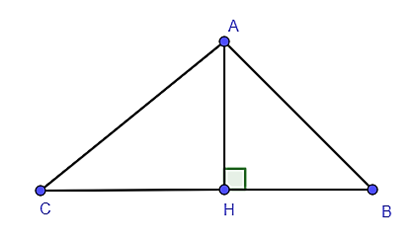
Ví dụ 2. Cho tam giác ABH vuông tại H có AB = 20 cm, BH = 12 cm. Trên tia đối của tia HB lấy điểm C sao cho $\text{AC}=\frac{5}{3}\text{AH}$. Chứng minh ΔABH ᔕΔCAH.

Hướng dẫn giải:

Ta có $\frac{\text{AB}}{\text{BH}}=\frac{20}{12}=\frac{5}{3},\frac{\text{AC}}{\text{AH}}=\frac{5}{3}$.

Suy ra $\frac{\text{AB}}{\text{BH}}=\frac{\text{AC}}{\text{AH}}$ hay $\frac{\text{AB}}{\text{AC}}=\frac{\text{BH}}{\text{AH}}$.

Xét hai tam giác ABH và CAH có:

$\widehat{\text{AHB}}=\widehat{\text{AHC}}=90°$

$\frac{\text{AB}}{\text{AC}}=\frac{\text{BH}}{\text{AH}}$

Suy ra ΔABH ᔕΔCAH (ch – cgv).

3. Bài tập tự luyện

Bài 1. Cho tam giác ABC có AB = 3 cm, AC = 5 cm, BC = 7 cm. Tam giác A'B'C' có A'B' = 6 cm, B'C' = 14 cm, A'C' = 10 cm. Khi đó tam giác BAC đồng dạng với:

A. Tam giác A'B'C';

B. Tam giác B'A'C';

C. Tam giác C'A'B';

D. Tam giác A'C'B'.

Bài 2. Cho tam giác ABC vuông tại A có BC = 10 cm, AC = 8 cm và tam giác DEF vuông tại D có EF = 5 cm, DF = 4 cm. Tỉ số chu vi của tam giác ABC và tam giác DEF là:

A. 1;

B. 2;

C. 3;

D. 4.

Bài 3. Cho tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A' có $\frac{\text{AB}}{\text{A'B'}}=\frac{\text{BC}}{\text{B'C'}}=3$. Khi đó $\frac{\text{C'A'}}{\text{CA}}$ bằng:

A. 3;

B. $\frac{2}{3}$;

C. $\frac{1}{3}$;

D. 2.

Bài 4. Cho tam giác ABC đồng dạng với tam giác DEF. Biết AB = 6 cm, BC = 10 cm, AC = 14 cm và chu vi tam giác DEF bằng 45 cm. Độ dài các cạnh của tam giác DEF là:

A. DE = 9 cm, EF = 15 cm, DF = 21 cm;

B. DE = 9 cm, EF = 21 cm, DF = 15 cm;

C. DE = 15 cm, EF = 9 cm, DF = 21 cm;

D. DE = 15 cm, EF = 21 cm, DF = 9 cm.

Bài 5. Cho tam giác ABC có AB = 4 cm, BC = 5 cm, AC = 6 cm và tam giác MNP có MN = 2 cm, NP = 3 cm, MP = 2,5 cm. Chọn đáp án đúng.

A. ΔABC ᔕΔNPM;

B. ΔABC ᔕΔMNP;

C. ΔABC ᔕΔMPN;

D. ΔABC ᔕΔNMP.

Bài 6. Tứ giác ABCD có AB = 3 cm, BC = 10 cm, CD = 12 cm, AD = 5 cm và BD = 6 cm. Tứ giác ABCD là hình gì?

A. Hình bình hành;

B. Hình thoi;

C. Hình thang;

D. Hình chữ nhật.

Bài 7. Cho tam giác ABC và một điểm O nằm trong tam giác đó. Gọi M, N, P lần lượt là trung điểm của các đoạn OA, OB, OC. Khi đó tam giác MNP đồng dạng với tam giác nào?

A. Tam giác ABC;

B. Tam giác OMN;

C. Tam giác OBC;

D. Tam giác OAB.

Bài 8. Cho tam giác ABC đồng dạng với tam giác DEF. Biết BC = 24,3 cm, CA = 32,4 cm, AB = 16,2 cm và AB – DE = 10 cm. Tính độ dài các cạnh của tam giác DEF.

A. DE = 6,2 cm, EF = 12,5 cm, DF = 9,3 cm;

B. DE = 6,2 cm, EF = 9,3 cm, DF = 12,4 cm;

C. DE = 6,2 cm, EF = 9,5 cm, DF = 11,2 cm;

D. DE = 6,2 cm, EF = 10 cm, DF = 8,9 cm.

Bài 9. Cho hình thang vuông ABCD tại A và D, AB = 6 cm, CD = 12 cm, AD = 17 cm. Trên cạnh AD lấy E, biết AE = 8 cm, EB = 10 cm, EC = 15 cm. Khi đó $\widehat{\text{BEC}}$ bằng

A. 60°;

B. 45°;

C. 90°;

D. 30°.

Bài 10. Cho tam giác ABC vuông tại A có AB = 3 cm, BC = 5 cm. Cho tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 1,5 cm. Độ dài cạnh B'C' là

A. 2 cm;

B. 2,25 cm;

C. 2,5 cm;

D. 3 cm.