Trường hợp đồng dạng thứ hai của tam giác lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Trường hợp đồng dạng thứ hai của tam giác lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Trường hợp đồng dạng thứ hai của tam giác.

Trường hợp đồng dạng thứ hai của tam giác lớp 8 (bài tập + lời giải)

1. Phương pháp giải

- Trường hợp đồng dạng thứ hai của tam giác (cạnh – góc – cạnh):

Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó bằng nhau thì hai tam giác đó đồng dạng.

∆ABC và ∆A'B'C' có $\frac{AB}{A\text{'}B\text{'}}=\frac{AC}{A\text{'}C\text{'}},\hat{A}=\widehat{A\text{'}}$ thì ∆ABC ᔕ ∆A'B'C'.

→ Để chứng minh hai tam giác đồng dạng bằng cách sử dụng trường hợp cạnh – góc – cạnh, ta thực hiện như sau:

Bước 1: Xét hai tam giác, chọn ra hai góc bằng nhau và chứng minh (nếu cần).

Bước 2: Lập tỉ số hai cạnh tạo nên mỗi góc đó rồi chứng minh hai tỉ số đó bằng nhau.

Bước 3: Kết luận hai tam giác đồng dạng (theo đúng thứ tự).

- Áp dụng trường hợp đồng dạng thứ hai vào tam giác vuông:

Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.

2. Ví dụ minh họa

Ví dụ 1. Cho tam giác ABC có AB = 6 cm, AC = 12 cm, $\widehat{\text{BAC}}=60°$ và tam giác MNP có MN = 2 cm, MP = 4 cm, $\widehat{\text{NMP}}=60°$. Chứng minh rằng ΔABC ᔕΔMNP.

Hướng dẫn giải:

Ta có $\frac{\text{AB}}{\text{MN}}=\frac{6}{2}=3,\frac{\text{AC}}{\text{MP}}=\frac{12}{4}=3$.

Suy ra $\frac{\text{AB}}{\text{MN}}=\frac{\text{AC}}{\text{MP}}$.

Xét hai tam giác ABC và MNP có: $\frac{\text{AB}}{\text{MN}}=\frac{\text{AC}}{\text{MP}}$

Suy ra ΔABC ᔕΔMNP (c – g – c).

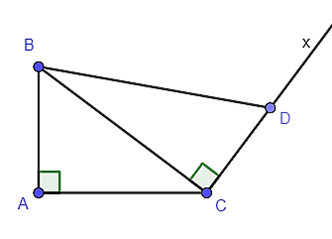
Ví dụ 2. Cho tam giác ABC vuông tại A có AC = 8 cm, AB = 6 cm, BC = 10 cm. Kẻ Cx vuông góc với BC (tia Cx và điểm A nằm khác phía so với đường thẳng BC). Lấy điểm D thộc Cx sao cho DC = $\frac{40}{3}$ cm. Chứng minh ΔABC ᔕΔCBD.

Hướng dẫn giải:

Ta có $\frac{\text{AB}}{\text{BC}}=\frac{6}{10}=\frac{3}{5},\frac{\text{AC}}{\text{CD}}=\frac{8}{\frac{40}{3}}=\frac{3}{5}$.

Suy ra $\frac{\text{AB}}{\text{BC}}=\frac{\text{AC}}{\text{CD}}$.

Xét hai tam giác ABC và CBD có:

$\widehat{\text{BAC}}=\widehat{\text{BCD}}=90°$

$\frac{\text{AB}}{\text{BC}}=\frac{\text{AC}}{\text{CD}}$

Suy ra ΔABC ᔕΔCBD (c – g – c).

3. Bài tập tự luyện

Bài 1. Cho góc xOy khác góc bẹt. Trên Ox lấy các điểm A và C, trên Oy lấy các điểm B và D sao cho OA ⋅ OD = OB ⋅ OC. Khẳng định nào sau đây là đúng?

A. ΔAOB ᔕΔCOD;

B. ΔABO ᔕΔCOD;

C. ΔBAO ᔕΔOCD;

D. ΔOBA ᔕΔDCO.

Bài 2. Cho hình thang ABCD (AB // CD), biết AB = 9 cm, BD = 12 cm, DC =16 cm. Tam giác BDC đồng dạng với tam giác nào dưới đây?

A. Tam giác ACD;

B. Tam giác ABC;

C. Tam giác ABD;

D. Cả A, B, C đều sai.

Bài 3. Cho tam giác ABC có AB = 10 cm, AC = 15 cm. Trên cạnh AB lấy D sao cho AD = 6 cm, trên cạnh AC lấy điểm E sao cho AE = 4 cm. Khẳng định nào sau đây là sai?

A. ΔABC ᔕΔAED;

B. $\widehat{\text{ABC}}=\widehat{\text{AED}}$;

C. $\widehat{\text{BCA}}=\widehat{\text{EDA}}$;

D. $\widehat{\text{AED}}=\widehat{\text{ACB}}$.

Bài 4. Cho hình thang vuông ABCD vuông tại A và D. Trên cạnh AD lấy I sao cho AB ⋅ DC = AI ⋅ DI. Khi đó $\widehat{\text{BIC}}$ bằng

A. 120°;

B. 90°;

C. 30°;

D. 75°.

Bài 5. Điền vào chỗ chấm. Cho hình thoi MNPQ có $\hat{\text{M}}=60°$. Qua P kẻ đường thẳng d bất kì cắt các tia đối của các tia NM, QM theo thứ tự tại E và F. Khi đó tam giác NQF đồng dạng với tam giác ……

A. MNQ;

B. ENQ;

C. MPF;

D. NEP.

Bài 6.Cho tam giác MNP có MN = 12 cm, MP = 15 cm, NP = 18 cm. Trên các cạnh MN, MP lần lượt lấy R, S sao cho MR = 10 cm và MS = 8 cm. Độ dài đoạn thẳng RS là

A. 12 cm;

B. 15 cm;

C. 14,2 cm;

D. 16,1 cm.

Bài 7. Cho tam giác ABC có AB = 9 cm, AC = 12 cm, BC = 7 cm. Khẳng định nào sau đây là đúng?

A. $\hat{\text{C}}=3\hat{\text{B}}$;

B. $\hat{\text{C}}=\frac{1}{3}\hat{\text{B}}$;

C. $\hat{\text{C}}=\frac{1}{2}\hat{\text{B}}$;

D. $\hat{\text{C}}=2\hat{\text{B}}$.

Bài 8. Cho tam giác MNP có MN = 18 cm, MP = 27 cm, NP = 30 cm. Gọi D là trung điểm của MN, E thuộc MP sao cho ME = 6 cm. Độ dài DE bằng

A. 8 cm;

B. 12 cm;

C. 9 cm;

D. 10 cm.

Bài 9. Cho hình thang ABCD (AB // CD), , AB = 2 cm, CD = 4,5 cm, BD = 3 cm. Khi đó BC vuông góc với

A. BD;

B. AD;

C. AC;

D. DC.

Bài 10. Cho hình bình hành ABCD, kẻ AH ⊥ CD tại H, AK ⊥ BC tại K. Tam giác KAH đồng dạng với tam giác nào dưới đây?

A. Tam giác ACK;

B. Tam giác ABH;

C. Tam giác ABC;

D. Tam giác AHC.