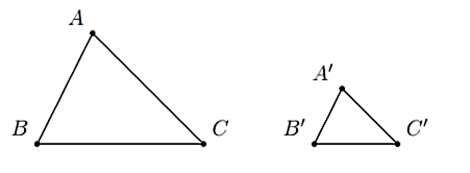Trường hợp đồng dạng thứ ba của tam giác lớp 8 (bài tập + lời giải)

Haylamdo biên soạn và sưu tầm bài viết phương pháp giải bài tập Trường hợp đồng dạng thứ ba của tam giác lớp 8 chương trình sách mới hay, chi tiết với bài tập tự luyện đa dạng giúp học sinh ôn tập, biết cách làm bài tập Trường hợp đồng dạng thứ ba của tam giác.

Trường hợp đồng dạng thứ ba của tam giác lớp 8 (bài tập + lời giải)

1. Phương pháp giải

- Trường hợp đồng dạng thứ ba của tam giác (góc – góc):

Nếu hai góc của tam giác này lần lượt bằng hai góc của tam giác kia thì hai tam giác đó đồng dạng.

∆ABC và ∆A'B'C' có $\hat{A}=\widehat{A\text{'}},\hat{B}=\widehat{B\text{'}}$ thì ∆ABC ᔕ ∆A'B'C'.

→ Để chứng minh hai tam giác đồng dạng bằng cách sử dụng trường hợp góc – góc, ta chứng minh hai tam giác có hai cặp góc bằng nhau.

- Áp dụng trường hợp đồng dạng thứ ba vào tam giác vuông:

Nếu tam giác vuông này có một góc nhọn bằng góc nhọn của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

2. Ví dụ minh họa

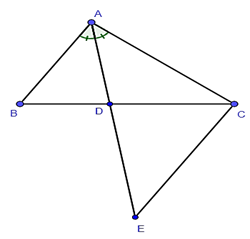
Ví dụ 1. Cho tam giác ABC có đường phân giác trong AD. Qua C kẻ đường thẳng song song với AB cắt tia AD tại E. Chứng minh ΔABD ᔕΔECD.

Hướng dẫn giải:

Vì CE // AB nên $\widehat{\text{CED}}=\widehat{\text{BAD}}$ (so le trong).

Xét hai tam giác ABD và ECD có:

$\widehat{\text{CED}}=\widehat{\text{BAD}}$

$\widehat{\text{ADB}}=\widehat{\text{EDC}}$ (đối đỉnh)

Suy ra ΔABD ᔕΔECD (g – g).

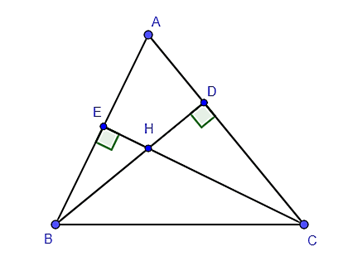
Ví dụ 2. Cho tam giác ABC có các đường cao BD và CE cắt nhau tại H. Chứng minh ΔBEH ᔕΔCDH.

Hướng dẫn giải:

Xét hai tam giác BEH và CDH có:

$\widehat{\text{BEH}}=\widehat{\text{CDH}}=90°$

$\widehat{\text{EHB}}=\widehat{\text{DHC}}$ (đối đỉnh)

Suy ra ΔBEH ᔕΔCDH (g – g).

3. Bài tập tự luyện

Bài 1. Cho tam giác ABC có AM là phân giác trong của tam giác. Kẻ tia Cx thuộc nửa mặt phẳng bờ BC không chứa A sao cho $\widehat{\text{BCx}}=\frac{1}{2}\widehat{\text{BAC}}$. Gọi N là giao điểm của Cx và AM. Khẳng định nào sau đây là đúng?

A. ΔANC ᔕΔMCN;

B. ΔANC ᔕΔAMC;

C. ΔABM ᔕΔANC;

D. ΔABM ᔕΔAMC.

Bài 2. Cho hình bình hành ABCD. Một đường thẳng bất kì đi qua A cắt BD tại E và cắt các đường thẳng BC, CD lần lượt tại F và G. Trong các khẳng định sau, khẳng định nào là sai?

A. ΔABF ᔕΔEGD;

B. ΔGCF ᔕΔGDA;

C. ΔGCF ᔕΔABF;

D. ΔABF ᔕΔGDA;

Bài 3. Cho tam giác ABC vuông tại A, đường cao AH. Khi đó BH ⋅ BC bằng

A. AB;

B. HC²;

C. AC²;

D. AB².

Bài 4. Cho tam giác ABC có đường phân giác trong AD. Gọi M và N theo thứ tự là hình chiếu của B và C trên đường thẳng AD. Khi đó tỉ số $\frac{\text{AB}}{\text{AC}}$ bằng tỉ số

A. $\frac{\text{AD}}{\text{CN}}$;

B. $\frac{\text{ND}}{\text{CN}}$;

C. $\frac{\text{BM}}{\text{CN}}$;

D. $\frac{\text{BD}}{\text{CN}}$.

Bài 5. Cho hình bình hành ABCD có AC > BD. Kẻ CE ⊥ AB tại E, CF ⊥ AD tại F, BH ⊥ AC tại H và DK ⊥ AC tại K. Khẳng định nào sau đây là đúng?

A. AD ⋅ AB + AE ⋅ AF = AC²;

B. AB ⋅ AF + AE ⋅ AD = AC²;

C. AD ⋅ AF + AE ⋅ AB = AC²;

D. AD ⋅ AF ⋅ AE ⋅ AB = AC².

Bài 6. Cho tam giác ABC và d là đường thẳng tùy ý qua B. Qua E là điểm bất kì trên AC, vẽ đường thẳng song song với AB và BC, lần lượt cắt d tại M và N. Gọi D là giao điểm của ME và BC. Đường thẳng NE cắt AB và MC lần lượt tại F và K. Khi đó tam giác AFN đồng dạng với tam giác nào dưới đây?

A. Tam giác MDC;

B. Tam giác DNC;

C. Tam giác ACM;

D. Tam giác NKB.

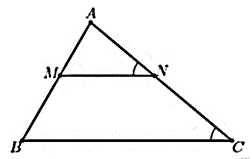
Bài 7. Cho hình vẽ sau. Khẳng định nào dưới đây là sai?

A. ΔAMN ᔕΔABC;

B. AM ⋅ AN = AC ⋅ AB;

C. MN // BC;

D. AM ⋅ AC = AN ⋅ AB.

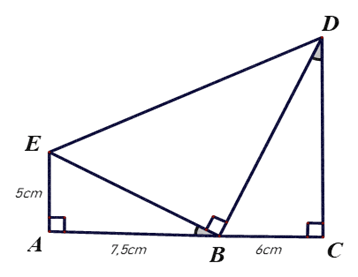
Bài 8. Cho hình vẽ, độ dài cạnh DC bằng

A. 7 cm;

B. 8 cm;

C. 9 cm;

D. 10 cm.

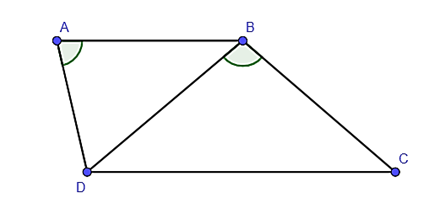
Bài 9. Cho hình thang ABCD (AB // CD) có $\widehat{\text{DAB}}=\widehat{\text{DBC}}$. Biết AB = 12 cm, DC = 18 cm. Độ dài BD (làm tròn đến hàng phần mười) là

A. 14,6 cm;

B. 14,7 cm;

C. 14,69 cm;

D. 14 cm.

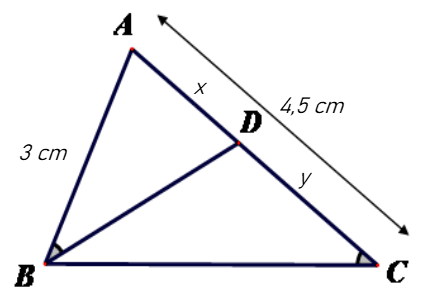
Bài 10. Cho hình vẽ sau. Độ dài x và y lần lượt là

A. x = 3 cm, y = 1,5 cm;

B. x = 1,5 cm, y = 3 cm;

C. x = 2,5 cm, y = 2 cm;

D. x = 2 cm, y = 2,5 cm.