Lý thuyết Góc ở tâm. Số đo cung hay, chi tiết | Toán lớp 9

Lý thuyết Góc ở tâm. Số đo cung hay, chi tiết

Tài liệu Lý thuyết Góc ở tâm. Số đo cung hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Góc ở tâm. Số đo cung từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Góc ở tâm

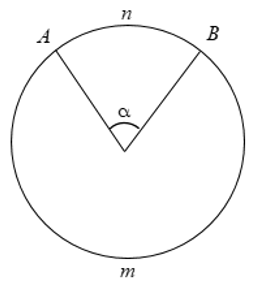
Góc có đỉnh trùng với tâm của đường tròn được gọi là góc ở tâm.

    + Hai cạnh của góc ở tâm cắt đường tròn tại hai điểm, do đó chia đường tròn thành hai cung.

     ⋅ Với các góc α ( 0 < α < 180°) thì cung nằm bên trong góc được gọi là cung nhỏ.

     ⋅ Cung nằm bên ngoài góc được gọi là cung lớn.

    + Cung AB được kí hiệu là .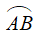

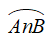
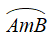
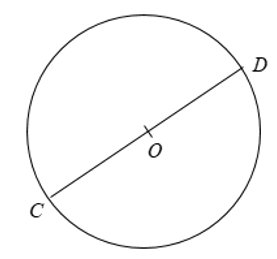
    + Cung là cung nhỏ, cung là cung lớn.

    + Với α = 180° thì mỗi cung là một nửa đường tròn.

    + Cung nằm bên trong góc gọi là cung bị chắn.

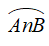
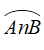
    + Cung là cung bị chắn bởi góc AOB hay góc AOB chắn cung nhỏ .

2. Số đo cung.

    + Số đo của cung nhỏ bằng số đo góc ở tâm chắn cung đó.

    + Số đo của cung lớn bằng hiệu giữa 360° và số đo cung nhỏ (có chung hai mút với cung lớn).

    + Số đo của nửa đường tròn bằng 180°

    + Kí hiệu số đo của cung AB là sđ .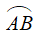

Ví dụ: Cho góc α = 100° là góc ở tâm O như hình vẽ. Tính số đo cung lớn.

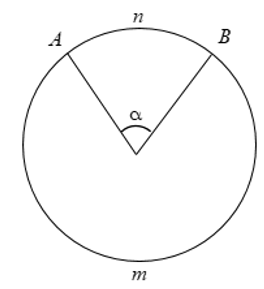
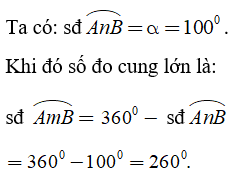
Chú ý:

    + Cung nhỏ có số đo nhỏ hơn 180°

    + Cung lớn có số đo lớn hơn 180°

    + Khi hai mút của cung trùng nhau, ta có “cung không” với số đo là 0° và cả đường tròn có số đo là 360°

3. So sánh hai cung.

    + Hai cung được gọi là bằng nhau nếu chúng có cùng số đo bằng nhau.

    + Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.

    + Kí hiệu: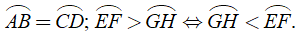

4. Khi nào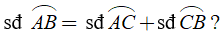

Nếu C là một điểm nằm trên cung AB thì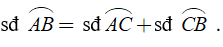

B. Bài tập tự luận

Câu 1: Cho hình vẽ sau:

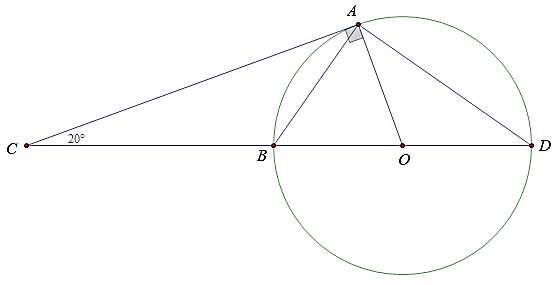
Tính số đo cung nhỏ AB, 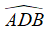từ đó so sánh cạnh AC và AD

Lời giải:

Ta có:

Câu 2: Dựa vào hình dưới, hình tính số đo của cung nhỏ AB, biết rằng B là trung điểm của OC

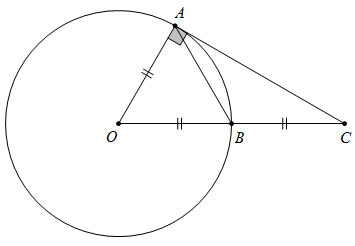
Lời giải:

Ta có tam giác ABC vuông tại A có B là trung điểm của OC

Suy ra OB = BC = AB

Mà OB = OA suy ra OB = OA = AB

Khi đó Δ OAB đều nên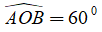

⇒ Số đo cung nhỏ AB bằng 60°