Bài tập Hệ thức lượng trong tam giác vuông cực hay, chọn lọc, có lời giải chi tiết | Toán lớp 9
Bài tập Hệ thức lượng trong tam giác vuông cực hay, chọn lọc, có lời giải chi tiết
Với Bài tập Hệ thức lượng trong tam giác vuông cực hay, chọn lọc, có lời giải chi tiết Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hệ thức lượng trong tam giác vuông từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Bài 1: Bộ ba nào sau đây không phải là độ dài 3 cạnh của tam giác vuông?
A. (6; 8; 10) B. (7; 24; 25)

Bài 2: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 5; AC = 7, BH = x, CH = y. Chỉ ra một hệ thức sai:
A. 52 = x2(x + y)2 B. 52 = x(x + y)
C. 72 = y(x + y) D. 52 + 72 = (x + y)2
Bài 3: Cho tam giác ABC vuông tại A, đường cao AH. Biết AC = 14, BC = 16, BH = x, CH = y. Chỉ ra một hệ thức sai:
A. 142 = y.16 B. 16 = x + y
C. xy = 16 D. A và B đúng
Bài 4: Cho tam giác MNP vuông tại M, đường cao MK. Biết MN = x, MP = y, NK = 2, PK = 6. Chỉ ra một hệ thức sai:
A. 82 = x2 + y2 B. x2 = 2.8
C. 6.8 = y2 D. x.y = 2.6
Bài 5: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = AC = y, AH = 5, BH = CH = x. Xác định x và y
A. x = 5; y = 5√2 B. x = √5; y = 5√2
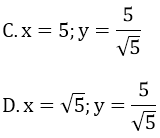
Bài 6: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 7, AC = 9, AH = x, BC = y. Chỉ ra một hệ thức sai:
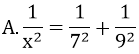
B. xy = 7.9
C. 72 + 92 = y2
D. 72 = x.y
Bài 7: Cho tam giác PQR vuông tại P, đường cao PS. Biết PS = 3, SQ = 2, SR = x, PR = y. Chỉ ra một hệ thức sai:
A. 3x = 2y B. y2 = x(x + 2)
C. x2 + 32 = y2 D. 32 = 2x
Bài 8: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = x, AC = y, AH = 2, BC = 5. Cạnh nhỏ nhất của tam giác này có độ dài là:
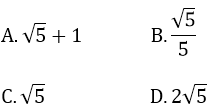
Bài 9: Cho tam giác ABC vuông tại A, sinB/sinC = ?
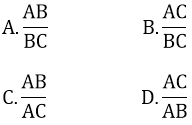
Bài 10: Cho tam giác ABC vuông tại A có góc B bằng B bằng 300, BC = 8. Độ dài AC là:
A.4 B.8√3
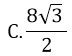
D. 2

Bài 11: Cho tam giác ABC vuông tại A. Biết AB = 6, tanB = 5/12 Độ dài AC là:
A.2 B. 5√2 C.5 D.2,5
Bài 12: Cho tam giác ABC vuông tại A. Chỉ ra một hệ thức sai:
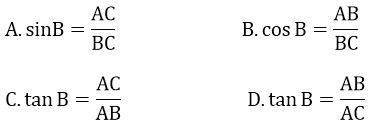
Bài 13: Cho cosα = 0,8. Tính sin α ( với α là góc nhọn)
A. sinα = 0,6 B. sinα = ±0,6
C. sinα = 0,4 D. Kết quả khác
Bài 14: Chỉ ra một hệ thức sai:
A.sin 250 = sin 700 B. tan 650.cot650 = 1
C.sin 300 = cos600 D.sin 750 = cos 750
Bài 15: Cho các biểu thức sau, biểu thức nào âm:
A. sin2 x + cos2 x B. sinx – 1
C. cosx + 1 D. sin 300
Bài 16: Cho tam giác ABC. Biết AB = 21, AC = 28, BC = 35. Tam giác ABC là tam giác gì?
A. Δ cân tại A B. Δ vuông ở A
C. Δ thường D. Cả 3 đều sai.
Bài 17:
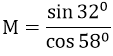
A. M = 1 B. M = -1 C. M = 0,5 D. M = √3/2
Bài 18: Cho ΔABC đều, đường cao AH. Biết HC = 3, độ dài AC và AH là:
A. AC = 3√3; AH = 4 B. AC = 6√3 ; AH = 6
C. AC = 6; AH = 3√3 D. Cả 3 đều sai
Bài 19: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 5; AC = 7. Độ dài AH là:
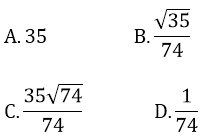
Bài 20: Cho tam giác ABC có góc B bằng 450, góc C bằng 300. Nếu AC = 8 thì AB bằng:
A. 4 B. 4√2 C. 4√3 D. 4√6

Đáp án và hướng dẫn giải
| 1. D | 2. A | 3. C | 4. D | 5. A |
| 6. D | 7. A | 8. C | 9. D | 10. A |
| 11. D | 12. D | 13. A | 14. A | 15. B |
| 16. B | 17. A | 18. C | 19. C | 20. B |
Bài 5:
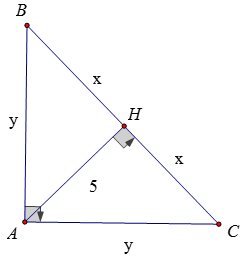
Ta có: AH2 = BH.CH ⇒ 52 = x2 ⇒ x = 5
AB.AC = AH.BC ⇔ y2 = 5.10 ⇔ y = 5√2
Bài 8:
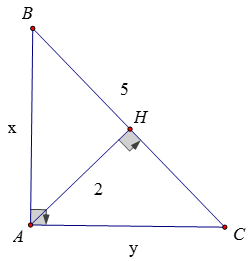
Ta có: x2 + y2 = 52 = 25 và xy = 5.2 = 10 (*)
⇒ (x + y)2 = 45 ⇒ x + y = 3√5 ⇒ x = 3√5 - y
Thay vào (*) ta được:
(3√5 - y)y = 10 ⇔ y = √5; y = 2√5
⇒ x = 2√5; x = √5
Vậy cạnh nhỏ nhất của tam giác là √5.
Bài 13:
sin2 α + cos2 α = 1 ⇒ sin2 α = 1 - 0,82 = 0,36
⇒ sinα = 0,6
Bài 17:
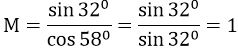
Bài 18:
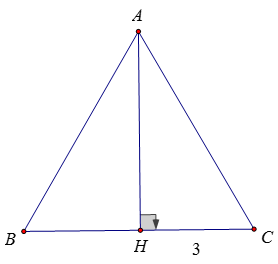
Xét tam giác AHC vuông tại H, góc ACH bằng 600 có:
AH = HC.tan600 = 3√3 (cm)
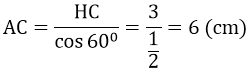

Bài 20:
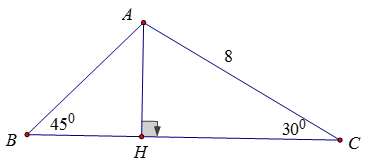
Kẻ đường cao AH của tam giác ABC
Xét tam giác AHC vuông tại H, góc ACH bằng 300 có:
AH = AC.sin300 = 4 (cm)
Xét tam giác AHB vuông tại H, góc ABH bằng 450 có:
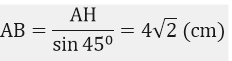
Bài 21:
Tam giác ABC vuông tại C có sinA = 2/3
sin2 A + cos2 A = 1 ⇒ cosA = √5/3
Do góc A cộng góc B bằng 900 nên
cosB = sinA = 2/3; sinB = cosA = √5/3
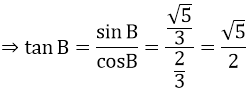
Bài 26:
Cho α, β là hai góc nhọn. Nếu α < β thì:
+) sinα < sinβ; tanα < tanβ
+) cosα > cosβ; cotα > cotβ
Do đó (I) và (III) đúng.
Bài 32:
Ta có: tanα.cotα = 1 nên sin2 α + cos2 α = tanα.cotα là đáp án đúng.
Bài 34:
cos770 = sin130
cos530 = sin370
cos270 = sin630
sin130 < sin240 < sin370 < sin570 < sin630 < sin750
⇒ cos770 < sin240 < cos530 < sin570 < cos270 < sin750
Bài 35:
Ta có: tan640 = cot260
tan470 = cot430
tan150 = cot750
cot30 > cot260 > cot370 > cot430 > cot430 > cot750
⇒ cot30 > tan640 > cot370 > tan470 > cot630 > tan150
Bài 36:
A = cos4x + cos2 x.sin2 x + sin2 x
= cos2 x(cos2 x + sin2 x) + sin2 x
= cos2 x + sin2 x = 1
Bài 21: Cho tam giác ABC vuông tại C có sinA = 2/3 thì tan B bằng
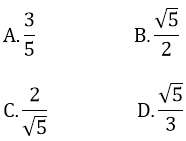
Bài 22: Cho hình 1. Chỉ ra một hệ thức sai:
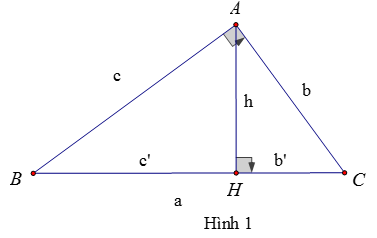
A. c2 = a.c' B. h2 = b'.c' C. b.c = a.h
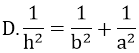
Bài 23: Cho một tam giác vuông có hai cạnh góc vuông là 6 cm và 8 cm. Độ dài đường cao xuất phát từ đỉnh góc vuông là:
A. 10 cm B. 4,8 cm C. 4,9 cm D. 5 cm
Bài 24: Đường cao của một tam giác vuông chia cạnh huyền thành hai đoạn có độ dài lần lượt là 4 và 9. Độ dài đường cao của tam giác vuông đó là:
A. 5 B. 6 C.7 D. 8
Bài 25: Gía trị của biểu thức B = cos620 - sin 280 là:
A. 0 B. 2 cos 620 C. 2 sin 280 D. 0,5

Bài 26: Ta có:
(I) sin 200 < sin300 < sin400
(II) cos 200 > cos300 > cos400
(III) tan100 < tan200 < tan300
A. Chỉ có (I) và (II) đúng B. Chỉ có (I) và (III) đúng
C. Chỉ có (II) và (III) đúng D. Cả (I), (II) và (III) đều đúng
Bài 27: ∆ABC vuông tại A, BC = 25, AC = 15. Số đo góc C bằng?
A. 510 B. 520 C. 530 D. 540
Bài 28: Cho tam giác ABC vuông tại A có BC = a, AC = b, AB = c. Khi đó:
A. b = asinB B. c = asinC C. b = acosC D. Cả 3 đều đúng
Bài 29: Với góc nhọn a ta có:
(I) 0 < sina < 1
(II) 0 < cosa < 1
(III) sin2a + cos2a = 1
A. Chỉ có (I) và (II) đúng B. Chỉ có (I) và (III) đúng
C. Chỉ có (II) và (III) đúng D. Cả (I), (II) và (III) đều đúng
Bài 30: Cho tam giác ABC vuông tại A, có 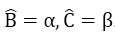
A.sin2α + cos2α = 1
B.sinα = cosβ
C.cosβ = sin(900 - α)
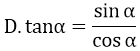
Bài 31: Trong một tam giác vuông, đường cao ứng với cạnh huyền là trung bình nhân của hai đoạn thẳng mà nó định ra trên cạnh huyền. Khẳng định trên đây ứng với công thức nào sau đây?
A. h = b.c
B. h2 = b'.c'
C. h2 = a.b
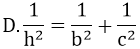
Bài 32: Cho α là góc nhọn, hệ thức nào sau đây là đúng:
A. sin2 α - cos2 α = 1
C. sin2 α + cos2 α = tanα.cotα
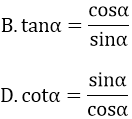
Bài 33: Góc nhọn α có cosα = 0,3865 thì số đo của góc α là:
A. 650 B. 670 C. 690 D. 710
Bài 34: Dãy số nào sau đây được sắp xếp theo thứ tự tăng dần
A. cos770 ; sin240 ; cos530 ; sin570 ; cos270 ; sin750
B. cos770 ; sin240 ; cos320 ; sin630 ; cos530 ; sin750
C. cos770 ; sin370 ; cos320 ; sin630 ; cos660 ; sin750
D. cos770 ; sin630 ; cos660 ; sin370 ; cos330 ; sin750
Bài 35: Dãy số nào sau đây được sắp xếp theo thứ tự giảm dần
A. cot30; tan640; cot370; cot630; tan470; tan150
B. cot30; cot370; tan640; tan470; cot630; tan150
C. cot30; tan470; cot630; tan640; cot370; tan150
D. cot30; tan640; cot370; tan470; cot630; tan150
Bài 36: Rút gọn biểu thức: A = cos4x + cos2x.sin2x + sin2x được kết quả là:
A.1 B.cos2 x C.sin2 x D.2
Bài 37: Một cái thang dài 4m, đặt dựa vào tường, góc giữa thang và mặt đất là 600. Khi đó, khoảng cách giữa chân thang đến tường bằng?
A. √3/2 m B. 2m C. 2√3 m D. 2√2 m
Bài 38: Cho tam giác ABC có góc A bằng 1050; góc B bằng 450; BC = 4. Tính AB
A. 0,5 B. 1 C. 1,46 D.2,07
Bài 39: Cho α + β = 900. Ta có:
A. sinα = sinβ
C. sin2 α + cos2 β = 1
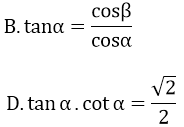
Bài 40: Tính cos2 200 + cos2 400 + cos2 500 + cos2 700
A. 1 B. 2 C.0 D. -1

Đáp án và hướng dẫn giải
| 21. B | 22. B | 23. D | 24. B | 25. A |
| 26. A | 27. C | 28. D | 29. D | 30. C |
| 31. B | 32. C | 33. B | 34. A | 35. D |
| 36. A | 37. B | 38. D | 39. B | 40. B |
Bài 21:
Tam giác ABC vuông tại C có sinA = 2/3
sin2 A + cos2 A = 1 ⇒ cosA = √5/3
Do góc A cộng góc B bằng 900 nên
cosB = sinA = 2/3; sinB = cosA = √5/3
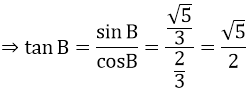
Bài 26:
Cho α, β là hai góc nhọn. Nếu α < β thì:
+) sinα < sinβ; tanα < tanβ
+) cosα > cosβ; cotα > cotβ
Do đó (I) và (III) đúng.
Bài 32:
Ta có: tanα.cotα = 1 nên sin2 α + cos2 α = tanα.cotα là đáp án đúng.
Bài 34:
cos770 = sin130
cos530 = sin370
cos270 = sin630
sin130 < sin240 < sin370 < sin570 < sin630 < sin750
⇒ cos770 < sin240 < cos530 < sin570 < cos270 < sin750
Bài 35:
Ta có: tan640 = cot260
tan470 = cot430
tan150 = cot750
cot30 > cot260 > cot370 > cot430 > cot430 > cot750
⇒ cot30 > tan640 > cot370 > tan470 > cot630 > tan150
Bài 36:
A = cos4x + cos2 x.sin2 x + sin2 x
= cos2 x(cos2 x + sin2 x) + sin2 x
= cos2 x + sin2 x = 1

