Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án | Toán lớp 9
Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án
Với Cách giải bài toán về diện tích hình học bằng cách lập phương trình cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải bài toán về diện tích hình học bằng cách lập phương trình từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải
bài toán về diện tích hình học
Bước 1: Lập phương trình.
- Chọn ẩn và đặt điều kiện cho ẩn (nếu có).
- Biểu diễn các đại lượng chưa biết theo ẩn và các đại lượng đã biết.
- Lập phương trình biểu thị mối quan hệ giữa các đại lượng.
Bước 2: Giải phương trình.
Bước 3: So sánh với điều kiện và kết luận.
Một số công thức tính diện tích thường gặp:
Diện tích tam giác: 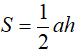
Diện tích hình vuông: S = a2 (a là độ dài cạnh góc vuông).
Diện tích hình chữ nhật: S = ab (a, b là chiều dài, chiều rộng của hình chữ nhật).
Diện tích hình tròn: S = πR2 (R là bán kính của hình tròn).
B. Các ví dụ điển hình
Ví dụ 1: Một mảnh đất hình chữ nhật có diện tích 720m2, nếu tăng chiều dài 6m và giảm chiều rộng 4m thì diện tích của mảnh vườn không đổi. Tính các kích thước của mảnh vườn đó.
Lời giải
Chọn D
Ví dụ 2:Một hình tròn nếu tăng bán kính thêm 5cm thì diện tích sẽ tăng gấp 2 lần. Tính bán kính của hình tròn đó (làm tròn đến hai chữ số thập phân).
Lời giải
Chọn A
Ví dụ 3: Tính độ dài các cạnh của một tam giác vuông, biết rằng chúng là ba số tự nhiên chẵn liên tiếp.
Lời giải
Chọn B

C. Bài tập vận dụng
Bài 1: Một tam giác vuông có cạnh huyền bằng 15cm. Chu vi của tam giác vuông bằng 36cm. Diện tích của tam giác đó là:
Lời giải:
Đáp án C
Bài 2: Một sân hình chữ nhật có chiều dài hơn chiều rộng là 3m. Nếu tăng chiều dài thêm 1m và tăng chiều rộng thêm 3m thì diện tích hình chữ nhật tăng gấp đôi. Tính chiều dài của hình chữ nhật đó.
Lời giải:
Đáp án C
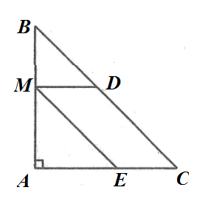
Bài 3: Cho tam giác ABC vuông cân tại A có AB = AC = 15cm. M là một điểm tùy ý thuộc AB. Từ M kẻ MD // AC, D ∈ BC và ME // BC, E ∈ AC. Tìm vị trí của điểm M để diện tích tứ giác MECD bằng 54cm2.
Lời giải:
Đáp án D
Bài 4: Một tam giác vuông có cạnh huyền bằng 15cm và diện tích bằng 54cm2. Chu vi của tam giác đó là:
Lời giải:
Đáp án A
Bài 5: Một hình chữ nhật có chu vi bằng 38cm và diện tích bằng 78cm2. Tìm chiều dài của hình chữ nhật đó.
Lời giải:
Đáp án A

Bài 6: Tìm độ dài cạnh của một tam giác đều, biết rằng nếu tăng độ dài mỗi cạnh của tam giác thêm 2cm thì diện tích của tam giác đều mới gấp 4 lần diện tích ban đầu.
Lời giải:
Đáp án C
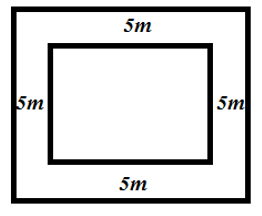
Bài 7: Trên mảnh đất hình chữ nhật có diện tích 1500m2, người ta xây một bể bơi hình chữ nhật xung quanh có lối đi dạo rộng 5m được lát gạch chống trơn. Biết diện tích của bể bơi đó bằng 50% diện tích của mảnh đất. Tính các kích thước của bể bơi.
Lời giải:
Đáp án D
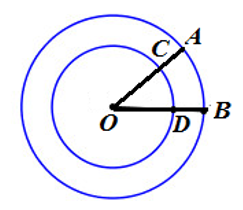
Bài 8: Hai đường tròn đồng tâm O có bán kính hơn kém nhau 5cm. Kẻ hai bán kính OA, OB của đường tròn lớn lần lượt cắt đường tròn nhỏ tại hai điểm C và D. Gọi diện tích của hình quạt tròn tạo bởi bán kính OC, OD và cung CD là S1, diện tích của hình quạt tròn tạo bởi bán kính OA, OB và cung AB là S2. Tìm đường kính của hình tròn nhỏ, biết 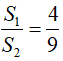
Lời giải:
Đáp án B
Bài 9: Một hình chữ nhật có chu vi là 70cm. Nếu giảm chiều rộng đi 5cm và tăng chiều dài thêm 20% thì bình phương độ dài đường chéo tăng 51cm. Tính diện tích của hình chữ nhật đó.
Lời giải:
Đáp án C
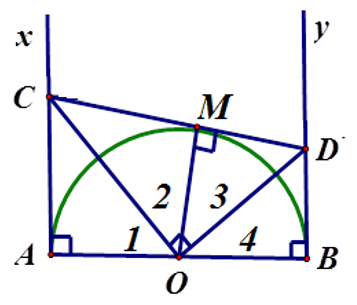
Bài 10: Cho nửa đường tròn (O) đường kính AB = 8cm. Gọi Ax, By là các tiếp tuyến tại A và B của (O). Tiếp tuyến tại điểm M tùy ý của (O) cắt Ax, By lần lượt tại C và D. Giả sử C ở vị trí để chu vi tứ giác ABCD bằng 28cm. Khi đó, diện tích tam giác AOC là:
Lời giải:
Đáp án A