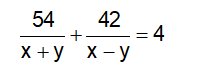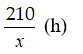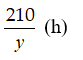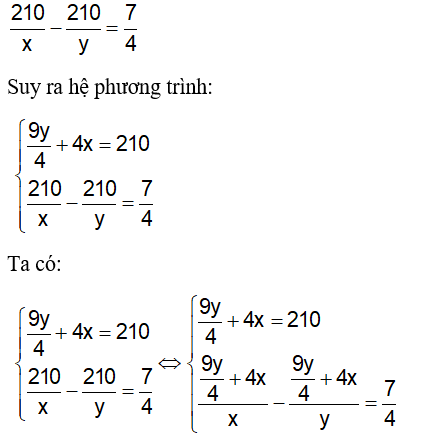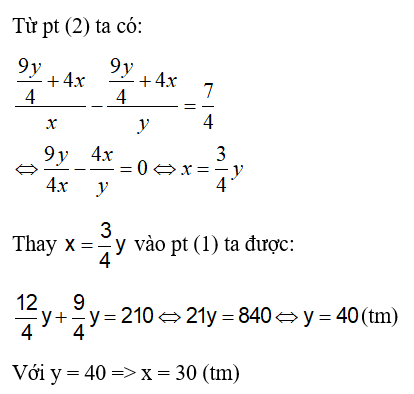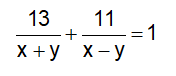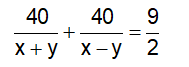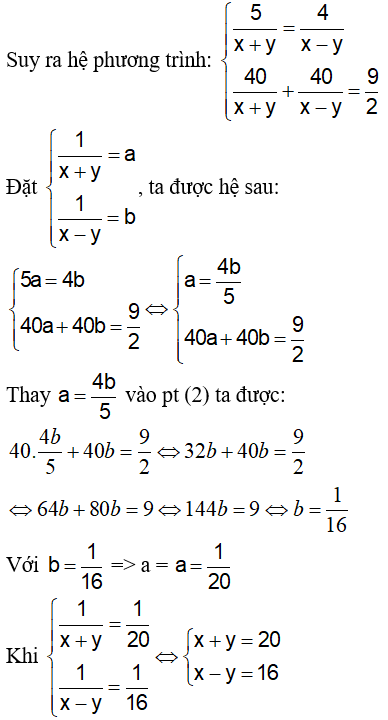Cách giải bài toán chuyển động cực hay | Giải bài toán bằng cách lập hệ phương trình | Toán lớp 9
Cách giải bài toán chuyển động cực hay | Giải bài toán bằng cách lập hệ phương trình
Với Cách giải bài toán chuyển động cực hay | Giải bài toán bằng cách lập hệ phương trình Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập chuyển động từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải
Các công thức cần nhớ:
S = V.T
Vxuôi = Vvật + Vnước, Vngược = Vvật – Vnước
B. Ví dụ minh họa
Ví dụ 1: Một ca nô dự định đi từ A đến B trong thời gian đã định. Nếu vận tốc ca nô tăng 3km/h thì ca nô đến sớm hơn 2 giờ. Nếu vận tốc ca nô giảm 3km/h thì ca nô đến muộn hơn 3 giờ. Tính chiều dài khúc sông.
Hướng dẫn giải:
Gọi vận tốc dự định của ca nô là x km/h (x >3)
Thời gian dự định đi là y giờ (y >2)
Quãng đường AB là : xy ( km)
Vì vận tốc ca nô tăng 3km/h thì ca nô đến sớm hơn 2 giờ, nên ta có phương trình:
(x +3)(y – 2) = xy
Vì vận tốc ca nô giảm 3km/h thì ca nô đến muộn hơn 3 giờ, nên ta có phương trình:
(x – 3)(y + 3) = xy
Suy ra ta có hệ phương trình:
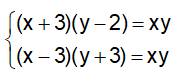
Ta có:
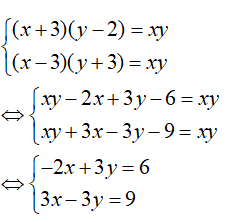
Cộng vế theo vế của hai phương trình ta được: x = 15 (tm)
Với x = 15 → y = (6 + 2.15): 3 = 12.( tm )
Vậy chiều dài khúc sông là 15 x 12 = 180 km.
Ví dụ 2: Một ca nô chạy trên sông trong 8h, xuôi dòng 81km và ngược dòng 105km. Một lần khác cũng chạy trên khúc sông đó ca nô này chạy trong 4h, xuôi dòng 54km và ngược dòng 42km. Hãy tính vận tốc xuôi và ngược dòng biết vận tốc dòng nước và vận tốc riêng của ca nô là không đổi.
Hướng dẫn giải:
Gọi vận tốc ca no khi nước yên lặng là x km/h.(x>y)
Gọi vận tốc của dòng nước là y km/h ( y > 0)
Vận tốc cano đi xuôi dòng là: x+ y ( km/h)
Vận tốc cano đi ngược dòng là: x – y ( km/h)
Vì ca nô chạy trên sông trong 8h, xuôi dòng 81km và ngược dòng 105km, ta có phương trình:
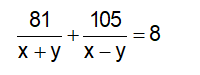
Vì ca nô chạy trên sông trong 4h, xuôi dòng 54km và ngược dòng 42km, ta có phương trình:
Cộng vế theo vế của hai phương trình trên ta được: 2x = 48 ⇔ x = 24 ( tm )
Với x = 24 → y = 3 ( tm )
Vậy vận tốc xuôi dòng là: 24 + 3 = 27 km/h
Vận tốc ngược dòng là 24 – 3 = 21km/h
Ví dụ 3: Trên quãng đường AB dài 210km tại cùng một thời điểm một xe máy khởi hành từ A đến B và một ô tô khởi hành đi từ B về A sau khi hai xe gặp nhau xe máy đi tiếp 4giờ nữa thì đến B, ô tô đi tiếp 2 giờ15 phút thì đến A. Biết rằng vận tốc của xe máy và ô tô là không đổi. Tính vận tốc của xe máy?
Hướng dẫn giải:
Gọi x, y (km/h) lần lượt là vận tốc của xe máy và ô tô ( x; y > 0)
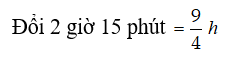
Quãng đường xe máy đi thêm 4 h và quãng đường ô tô đi trong 2 giờ 15 phút bằng độ dài quãng đường AB nên
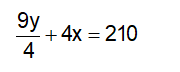
Thời gian xe máy đi hết quãng đường AB là
Thời gian ô tô đi hết quãng đường AB là
Vì ban đầu hai xe khởi hành cùng 1 lúc nên:

C. Bài tập trắc nghiệm
Câu 1: Một ca nô chạy trên sông trong 5h, xuôi dòng 78km và ngược dòng 44km. Với vận tốc dự định nếu ca nô xuôi dòng 13km và ngược dòng 11km với vận tốc dự định đó thì mất 1 giờ. Hãy tính vận tốc riêng của ca nô,biết vận tốc dòng nước và vận tốc riêng của ca nô là không đổi.
A. 24km/h
B. 36km/h
C. 72km/h
D.54km/h
Lời giải:
Đáp án: A
Gọi vận tốc ca no khi nước yên lặng là x km/h.(x>y)
Gọi vận tốc của dòng nước là y km/h (y > 0)
Vận tốc ca no đi xuôi dòng là: x+y (km/h)
Vận tốc ca no đi ngược dòng là: x-y (km/h)
Vì ca nô chạy trên sông trong 5h, xuôi dòng 78km và ngược dòng 44km, ta có phương trình:
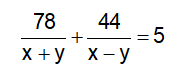
Vì ca nô chạy trên sông trong 1h, xuôi dòng 13km và ngược dòng 11km, ta có phương trình:
Cộng vế theo vế của hai phương trình trên ta được: 2x = 48 ⇔ x = 24 ( tm )
Với x = 24 → y = 2 ( tm )
Vậy vận tốc riêng của ca nô là 24km/h.
Câu 2: Một ô tô đi quãng đường AB với vận tốc 50km/h rồi đi tiếp quãng đường BC với vận tốc 45km/h. Biết quãng đường tổng cộng dài 165km và thời gian xe đi trên quãng đường AB ít hơn thời gian trên quãng đường BC là 30 phút. Tính thời gian ô tô đi trên quãng đường AB.
A. 1 giờ
B. 1,5 giờ
C. 2 giờ
D. 2,5 giờ
Lời giải:
Đáp án: B
Gọi thời ô tô đi trên quãng đường AB và BC lần lượt là x (giờ), y (giờ) (x,y > 0)
Đổi 30 phút = 0,5h
Vì tổng độ dài quãng đường là 165km, nên ta có phương trình: 50x + 45y = 165
Vì thời gian xe đi trên quãng đường AB ít hơn thời gian trên quãng đường BC là 30 phút, ta có: x + 0,5 = y

thay y = x + 0,5 vào pt (1) ta được:
50x + 45(x + 0,5) = 165 ⇔ 95x + 22,5 = 165
⇔ 95x = 142,5 ⇔ x = 1,5 ( tm )
Với x = 1,5 → y = 2 (tm )
Vậy vận tốc của ô tô trên AB là: 1,5 giờ. Chọn đáp án B.
Câu 3: Một người đi xe đạp từ địa điểm A đến B trong một thời gian đã định với vận tốc không đổi. Nếu người đó tăng vận tốc lên 3km/h thì đến B sớm hơn dự định 1 giờ. Nếu người đó giảm vận tốc 2km/h thì đến B muộn hơn dự định 1 giờ. Tính quãng đường AB.
A. 40km B. 50km C. 60km D. 70km
Lời giải:
Đáp án: C
Gọi vận tốc dự định là x (km/h), thời gian dự định là y (giờ) (x > 0, y > 0)
Độ dài quãng đường AB là : xy ( km)
Vì người đó tăng vận tốc lên 3 km/h thì sẽ đến B sớm hơn dự định 1 giờ, tức là nếu đi với vận tốc x + 3 km/h thì thời gian là y -1 giờ. Khi đó độ dài quãng đường là (x + 3)(y – 1).
Vì người đó giảm vận tốc 2 km/h thì sẽ đến B muộn hơn dự định 1 giờ, tức là nếu đi với vận tốc x-2 km/h thì thời gian là y + 1 giờ. Khi đó độ dài quãng đường là (x – 2)(y + 1).

Cộng vế theo vế của hai phương trình ta được: y = 5 (tm)
Với y = 5 → x = (2 + 2.5) = 12.( tm )
Vậy quãng đường AB là 5 x 12 = 60km.
Câu 4: Hai ô tô cùng khởi hành một lúc từ 2 tỉnh A và B cách nhau 400km đi ngược chiều và gặp nhau sau 5giờ. Nếu vận tốc của mỗi xe không thay đổi nhưng xe đi chậm xuất phát trước xe kia 40 phút thì 2 xe gặp nhau sau 5 giờ 22 phút kể từ lúc xe chậm khởi hành. Tính vận tốc xe chạy chậm.
A. 44 B. 54 C. 60 D. 36
Lời giải:
Đáp án: D
Gọi vận tốc của xe nhanh là x (km/h), vận tốc của xe chậm là là y (km/h)(x,y>0)
Hai xe cùng khởi hành một lúc và đi ngược chiều sau 5h gặp nhau, nên ta có phương trình: 5(x+y) = 400

Thay x = 80 – y vào pt (2) ta được:
141(80 – y) + 161y = 12000
⇔ 11280 – 141y + 161y = 12000 ⇔ 20y = 720 ⇔ y = 36
Với y = 36 → x = 80 – 36 = 44 (tm).
Vậy vận tốc xe chạy chậm là 36 km/h.
Câu 5: Một chiếc thuyền xuôi dòng, ngược dòng trên khúc sông dài 40km hết 4 giờ 30 phút. Biết thời gian xuôi dòng 5km bằng thời gian ngược dòng 4km. Tính vận tốc dòng nước?
A. 1 B. 2 C. 3 D. 4
Lời giải:
Đáp án: B
Gọi vận tốc của thuyền khi dòng nước yên lặng là: x (km/h), (x > y)
Vận tốc của dòng nước là y (km/h), (y > 0)
Vận tốc của thuyền khi xuôi dòng là: x + y ( km/h)
Vận tốc của thuyền khi ngược dòng là: x - y ( km/h)
Vì thời gian xuôi dòng 5km bằng thời gian ngược dòng 4km, nên ta có phương trình:
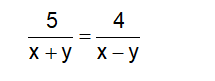
Vì thuyền xuôi dòng, ngược dòng trên khúc sông dài 40km hết 4 giờ 30 phút = 9/2 giờ, ta có:
Cộng vế theo vế của hai phương trình trên ta được: 2x = 36 ⇔ x = 18 ( tm )
Với x = 18 → y = 2 ( tm )
Vậy vận tốc của dòng nước là 2 km/h.

Câu 6: Một ô tô đi từ A đến B với tốc xác định, trong thời gian đã định. Nếu vận tốc giảm 10km/h thì thời gian tăng lên 45 phút, nếu vận tốc tăng 10km/h thì thời gian giảm 30 phút. Thời gian dự định của ô tô?
A. 1 B.2 C. 3 D.4
Lời giải:
Đáp án: C
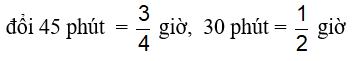
Gọi vận tốc dự đinh của ô tô là x (km/h), ( x > 10)
Thời gian dự định của ô tô là y (km/h) ( y > 0,5)
Vì vận tốc giảm 10km/h thì thời gian tăng lên 45 phút, nên ta có:
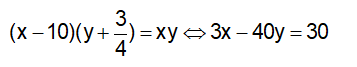
Vì vận tốc tăng 10km/h thì thời gian giảm 30 phút, nên ta có:
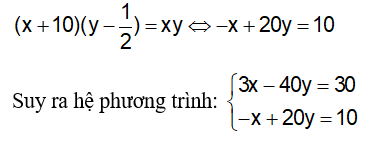
Nhân pt (2) với 3 ta được: –3x + 60y = 30, rồi cộng với pt (1) ta được:
20y = 60 ⇔ y = 3 ( tm)
Với y = 2 → x = 50 ( tm)
Vậy thời gian dự đinh của ô tô là: 3 giờ.
Câu 7: Một ô tô và xe đạp chuyển động từ hai đầu một quãng đường, Sau 3 giờ thì hai xe gặp nhau, nếu chuyển động cùng chiều và xuất phát tại cùng một địa điểm thì sau 1 giờ hai xe cách nhau 28km. Tính vận tốc xe đạp biết quãng đường dài 156 km.
A. 12 B. 24 C. 36 D. 42
Lời giải:
Đáp án: A
Gọi vận tốc của xe đạp và ô tô lần lượt là x (km/h) và y (km/h), ( x, y > 0)
Vì sau 3 giờ thì hai xe gặp nhau, nên ta có phương trình: 3x + 3y = 156
Vì sau 1 giờ hai xe cách nhau 28km, khi xuất phát tại một điểm, ta có phương trình: y – x = 28
Suy ra hệ phương trình:
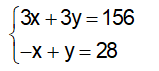
Nhân pt (2) với 3 ta được: –3x + 3y = 84, rồi cộng với pt(1) ta được:
6y = 240 ⇔ y = 40 (tm )
Với y = 40 → x = 12 (tm )
Vậy vận tốc của xe đạp là 12 km/h
Câu 8: Một ô tô dự định đi từ A đến B với thời gian nhất định. Nếu chạy với vận tốc 35km/h thì đến B chậm hơn 2 giờ so với dự định. Nếu chạy với vận tốc 50km/h thì đến B sớm hơn 1 giờ so với dự định. Tính quãng đường AB?
A. 250 B. 350 C. 420 D. 360
Lời giải:
Đáp án: B
Gọi quãng đường AB là x (km), thời gian dự định ô tô đi từ A đến B là y (giờ), ( x > 0, y > 1)
Vì nếu chạy với vận tốc 35km/h thì đến B chậm hơn 2 giờ so với dự định, ta có phương trình:
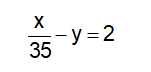
Vì nếu chạy với vận tốc 50km/h thì đến B sớm hơn 1 giờ so với dự định, ta có:
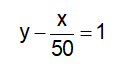
Suy ra hệ phương trình:
Cộng pt(1) và pt (2) ta được:
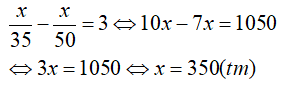
Với x = 350 => y = 8 (tm )
Vậy quãng đường AB dài 350km
Câu 9: Hai ca nô đi ngược chiều nhau và khởi hành cùng lúc trên dòng sông dài 85km. Sau 1 giờ 40 phút thì gặp nhau. Tính vận tốc thật của mỗi ca nô, biết rằng vận tốc ca nô xuôi dòng lớn hơn vận tốc ca nô ngược dòng là 9km/h, và vận tốc dòng nước là 3km/h.
A. 27km/h và 24km/h
B. 30km/h và 36km/h
C. 36km/h và 40km/h
D. 42km/h và 48km/h
Lời giải:
Đáp án: A
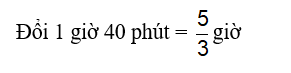
Gọi vận tốc thật của ca nô xuôi dòng là x (km/h), (x > 3)
Vận tốc ca nô ngược dòng là y (km/h),(y > 3)
Vì hai ca nô đi ngươc chiều nhau và khời hành cùng lúc trên dòng sông dài 85km, ta có:
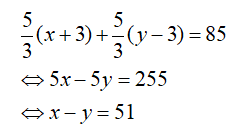
Vì vận tốc ca nô xuôi dòng lớn hơn vận tốc ca nô ngược dòng là 9km/h, ta có:
(x+3)-(y-3)=9 ⇔ x-y=3
Suy ra hệ phương trình:
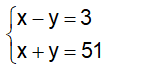
Cộng hai phương trên với nhau ta được: 2x = 54 ⇔ x = 27 (tm)
Với x = 27 → y = 24 ( tm)
Vậy vận tốc thực của ca nô xuôi dòng là 27km/h và vận tốc ca nô ngược dòng là 24km/h.
Câu 10: Hai tỉnh A và B cách nhau 180km, cùng một lúc ô tô đi từ A đến B và xe máy đi từ B về A. Hai xe gặp nhau tại thị trấn C, từ C đến B ô tô đi hết 2 giờ còn từ C về A xe máy đi hết 4 giờ 30 phút. Tính vận tốc của ô tô, biết rằng hai xe chạy trên AB không đổi.
A. 24km/h
B. 48km/h
C. 36km/h
D. 54km/h
Lời giải:
Đáp án: C
Đổi 4 giờ 30 phút = 4,5 giờ
Gọi vận tốc của ô tô là x (km/h), vận tốc của xe máy là y (km/h), (x, y > 0)
Vì hai xe gặp nhau tại thị trấn C, từ C đến B ô tô đi hết 2 giờ còn từ C về A xe máy đi hết 4 giờ 30 phút = 4,5 h , ta có phương trình: 2x + 4,5y = 180.
Vì hai xe đi cùng một lúc và gặp nhau tại thị trấn C nên thời gian hai xe đến C là như nhau, ta có:
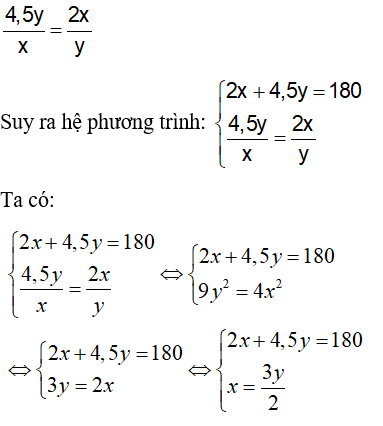
Thay x = 1,5 y vào pt (1) ta có:
2.(1,5 y) + 4,5y = 180 ⇔ 3y + 4,5y = 180 ⇔ 7,5 y = 180 ⇔ y = 24 ( tm )
Với y = 24 → x = 36 ( tm)
Vậy vận tốc của ô tô là 36 km/h.