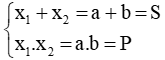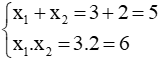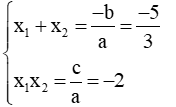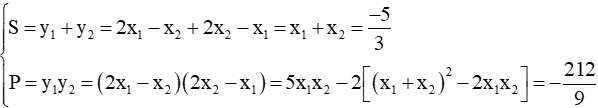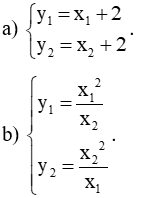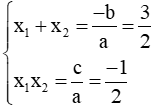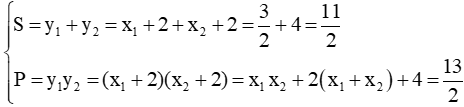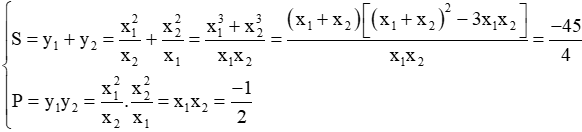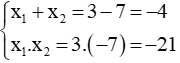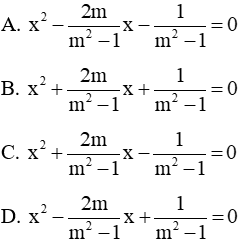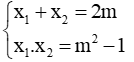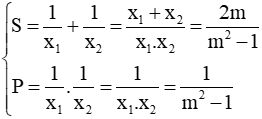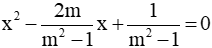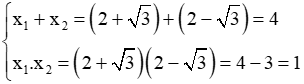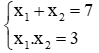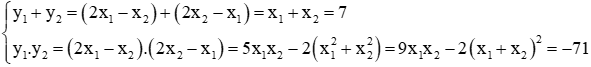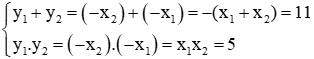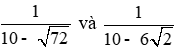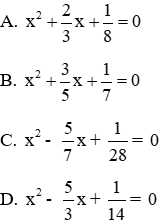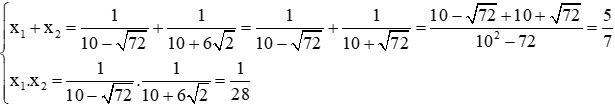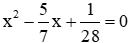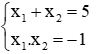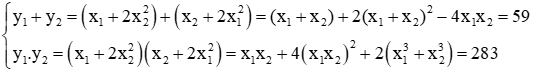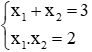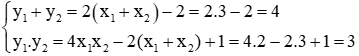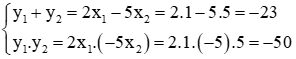Cách lập phương trình bậc hai khi biết hai nghiệm của phương trình đó | Toán lớp 9

Cách lập phương trình bậc hai khi biết hai nghiệm của phương trình đó

Với Cách lập phương trình bậc hai khi biết hai nghiệm của phương trình đó Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập lập phương trình bậc hai khi biết hai nghiệm của phương trình đó từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

- Bài toán: Lập phương trình bậc hai ẩn x có 2 nghiệm: x₁ = a, x₂ = b

- Cách giải:

+ Tính

+ Kết luận: x₁, x₂ là nghiệm của phương trình x² - Sx + P = 0

Ví dụ 1: Lập phương trình bậc hai ẩn x có 2 nghiệm: x₁ = 3, x₂ = 2

Giải

Ta có:

Suy ra x₁ = 3, x₂ = 2 là hai nghiệm của phương trình x² - 5x + 6 = 0

Ví dụ 2: Gọi x₁, x₂ là hai nghiệm của phương trình: 3x² + 5x - 6 = 0. Không giải phương trình hãy lập phương trình bậc hai ẩn y có hai nghiệm y₁, y₂ thỏa mãn y₁ = 2x₁ - x₂ và y₂ = 2x₂ - x₁.

Giải

Xét phương trình có 3x² + 5x - 6 = 0 có a.c = 3.(-6) < 0 nên phương trình đã cho có hai nghiệm phân biệt.

Theo Vi-et ta có:

Vậy phương trình bậc hai có hai nghiệm y₁, y₂ là: .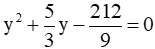

Ví dụ 3: Gọi x₁, x₂ là hai nghiệm của phương trình: 2x²-3x-1 = 0. Không giải phương trình hãy lập phương trình bậc hai ẩn y có hai nghiệm y₁, y₂ thỏa mãn

Giải

Xét phương trình 2x²-3x-1 = 0 có a.c = 2.(-1) = -2 < 0 nên phương trình đã cho có hai nghiệm phân biệt.

Theo hệ thức Vi-et ta có:

a) Ta có:

Vậy phương trình bậc hai có hai nghiệm y₁, y₂ là: .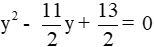

b) Ta có:

Vậy phương trình bậc hai có hai nghiệm y₁, y₂ là: .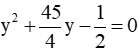

B. Bài tập

Câu 1: Phương trình bậc hai ẩn x có hai nghiệm là 3 và -7

A. x² + 4x – 21 = 0

B. x² - 4x – 21 = 0

C. x² + 4x + 21 = 0

D. x² - 4x + 21 = 0

Giải

Ta có:

Suy ra x₁ = 3, x₂ = -7 là hai nghiệm của phương trình x² + 4x - 21 = 0

Đáp án đúng là A

Câu 2: Phương trình bậc hai ẩn x có hai nghiệm là 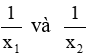biết x₁, x₂ là hai nghiệm của phương trình x² - 2mx + m² - 1 = 0 là

Giải

Vì x₁, x₂ là hai nghiệm của phương trình: x² - 2mx + m² - 1 = 0 nên

Ta có:

Với hai nghiệm là 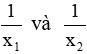thì

Suy ra hai số 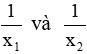là nghiệm của phương trình

Đáp án đúng là D

Câu 3: Phương trình bậc hai ẩn x có hai nghiệm là

A. x² + 4x – 1 = 0

B. x² - 4x – 1 = 0

C. x² + 4x + 1 = 0

D. x² - 4x + 1 = 0

Giải

Ta có:

Suy ra 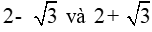là hai nghiệm của phương trình x² - 4x + 1 = 0

Đáp án đúng là D

Câu 4: Lập phương trình bậc hai ẩn y có hai nghiệm y₁ = 2x₁ – x₂ và y₂ = 2x₂ – x₁, biết x₁, x₂ là hai nghiệm của phương trình x² - 7x + 3 = 0

A. y² + 7y + 71 = 0

B. y² – 7y - 71 = 0

C. y² – 7y + 71 = 0

D. y² + 7y - 71 = 0

Giải

Phương trình x² - 7x + 3 = 0 có ∆ = (-7)² – 4.1.3 = 37 > 0 nên có 2 nghiệm x₁, x₂

Ta có:

Với hai nghiệm y₁ = 2x₁ – x₂ và y₂ = 2x₂ – x₁ thì

Suy ra y₁, y₂ là hai nghiệm của phương trình y² - 7y - 71 = 0

Đáp án đúng là B

Câu 5: Biết x₁, x₂ là hai nghiệm của phương trình x² + 11x + 5 = 0. Lập phương trình bậc hai ẩn y có hai nghiệm là số đối của x₁, x₂

A. y² + 8y + 1 = 0

B. y² - 7y - 21 = 0

C. y² - 11y + 5 = 0

D. y² + y - 1 = 0

Giải

Phương trình x² + 11x + 5 = 0 có hai nghiệm x₁, x₂ nên

Với hai nghiệm y₁ = -x₁ và y₂ = -x₂ thì

Suy ra y₁, y₂ là hai nghiệm của phương trình y² – 11y + 5 = 0

Đáp án đúng là C

Câu 6: Phương trình bậc hai ẩn x có hai nghiệm là

Giải

Ta có:

Suy ra 2 số đã cho là hai nghiệm của phương trình:

Đáp án đúng là C

Câu 7: Lập phương trình bậc hai ẩn y có hai nghiệm y₁ = x₁ + 2x₂² và y₂ = x₂ + 2x₁², biết x₁, x₂ là hai nghiệm của phương trình x² - 5x - 1 = 0

A. y² - 59y + 283 = 0

B. y² - 17y + 171 = 0

C. y² - 7y + 370 = 0

D. y² + 8y - 17 = 0

Giải

Phương trình x² - 5x - 1 = 0 có hai nghiệm x₁, x₂ nên

Với hai nghiệm y₁ và y₂ thì:

Suy ra y₁, y₂ là hai nghiệm của phương trình y² - 59y + 283 = 0

Đáp án đúng là A

Câu 8: Lập phương trình bậc hai ẩn y có hai nghiệm y₁ = 2x₁-1 và y₂ = 2x₂-1, biết x₁, x₂ là hai nghiệm của phương trình x² - 3x + 2 = 0

A. y² - 5y + 3 = 0

B. y² - 4y + 3 = 0

C. y² - 2y + 4 = 0

D. y² + 8y - 7 = 0

Giải

Phương trình x² - 3x + 2 = 0 có hai nghiệm x₁, x₂ nên

Với hai nghiệm y₁ và y₂ thì

Vậy y₁, y₂ là nghiệm của phương trình y² – 4y + 3 = 0

Đáp án B

Câu 9: Lập phương trình bậc hai ẩn y có hai nghiệm y₁ = 2x₁ và y₂ = -5x₂, biết x₁, x₂ là hai nghiệm của phương trình x² - 6x + 5 = 0 (x₁ < x₂)

A. y² - 23y + 50 = 0

B. y² - 23y + 5 = 0

C. y² + 23y - 50 = 0

D. y² + 23y - 7 = 0

Giải

Phương trình x² - 6x + 5 = 0 có a + b + c = 1 – 6 + 5 = 0 nên có hai nghiệm x₁ = 1, x₂ = 5

Với hai nghiệm y₁ và y₂ thì

Vậy y₁, y₂ là nghiệm của phương trình y² + 23y - 50 = 0

Đáp án C