Lý thuyết Công thức nghiệm của phương trình bậc hai hay, chi tiết | Toán lớp 9

Lý thuyết Công thức nghiệm của phương trình bậc hai hay, chi tiết

Tài liệu Lý thuyết Công thức nghiệm của phương trình bậc hai hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Công thức nghiệm của phương trình bậc hai từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Công thức nghiệm

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) và biệt thức Δ = b² - 4ac

    + Nếu Δ > 0 thì phương trình có hai nghiệm phân biệt

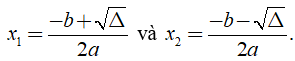
    + Nếu Δ = 0 thì phương trình có nghiệm kép là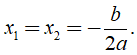

    + Nếu Δ < 0 thì phương trình vô nghiệm.

Chú ý: Nếu phương trình ax² bx + c = 0 (a ≠ 0) có a và c trái dấu, tức là ac < 0. Khi đó ta có Δ = b² - 4ac > 0 ⇒ Phương trình luôn có hai nghiệm phân biệt

2. Ví dụ cụ thể

Câu 1: Giải phương trình x² - 5x + 4 = 0

Hướng dẫn:

    + Tính Δ = (-5)² - 4.4.1 = 25 - 16 = 9 > 0

    + Do Δ > 0 , phương trình có hai nghiệm là:

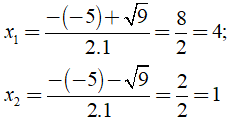
Vậy phương trình có hai nghiệm là x₁ = 4; x₂ = 1

Câu 2: Giải phương trình 5x² - x + 2 = 0

Hướng dẫn:

    + Tính Δ = (-1)² - 4.5.2 = -39 < 0

    + Do Δ < 0, phương trình đã cho vô nghiệm

Vậy phương trình đã cho vô nghiệm

Câu 3: Giải phương trình x² - 4x + 4 = 0.

Hướng dẫn:

    + Tính Δ = (-4)² - 4.4.1 = 16 - 16 = 0.

    + Do Δ = 0, phương trình có nghiệm kép là x₁ = x₂ = -4/(2.1) = 2

Vậy phương trình có nghiệm kép là x = 2

B. Bài tập tự luận

Câu 1: Giải phương trình x² + 14x + 49 = 0; x² - 2x - 5 = 0

Lời giải:

Câu 2: Cho phương trình -x² + 2x + 2017²⁰¹⁷ = 0 . Không giải phương trình, hãy cho biết phương trình đã cho có bao nhiêu nghiệm?

Lời giải:

Ta có: Δ=b² - 4ac

Nhận thấy: b² > 0; ac = -2017²⁰¹⁷ < 0 ⇒ -4ac > 0

Do đó: Δ = b² - 4ac > 0

⇒ Phương trình đã cho có hai nghiệm phân biệt

Vậy phương trình đã cho có hai nghiệm phân biệt