Tổng hợp lý thuyết Chương 2 Hình học 9 hay, chi tiết | Toán lớp 9
Tổng hợp lý thuyết Chương 2 Hình học 9 hay, chi tiết
Tài liệu Tổng hợp lý thuyết Chương 2 Hình học 9 hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Chương 2 Hình học từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Định nghĩa về đường tròn
Đường tròn tâm O bán kính R > 0 là hình gồm các điểm cách điểm O một khoảng R kí hiệu là (O; R) hay (O).
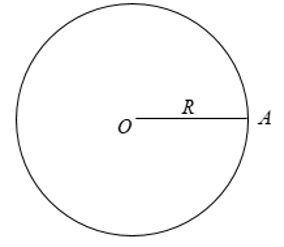
Nếu A nằm trên đường tròn (O; R) thì OA = R.
Nếu A nằm trong đường tròn (O; R) thì OA < R.
Nếu A nằm ngoài đường tròn (O; R) thì OA > R.
2. Quan hệ vuông góc giữa đường kính và dây
+ Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy.
+ Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
3. Liên hệ giữa dây và khoảng cách từ tâm đến dây
+ Trong một đường tròn:
⋅ Hai dây bằng nhau thì cách đều tâm.
⋅ Hai dây cách đều tâm thì bằng nhau.
+ Trong hai dây của một đường tròn:
⋅ Dây nào lớn hơn thì dây đó gần tâm hơn.
⋅ Dây nào gần tâm hơn thì dây đó lớn hơn.

4. Vị trí tương đối của đường thẳng và đường tròn
Cho đường tròn (O; R) và đường thẳng Δ. Đặt d = d(O, Δ).
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa d và R |
| Đường thẳng và đường tròn cắt nhau | 2 | d < R |
| Đường thẳng và đường tròn tiếp xúc nhau | 1 | d = R |
| Đường thẳng và đường tròn không giao nhau | 0 | d > R |
5. Dấu hiệu nhận biết tiếp tuyến của đường tròn
+ Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
+ Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn.
6. Tính chất của hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
+ Điểm đó cách đều hai tiếp điểm.
+ Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
+ Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
7. Đường tròn nội tiếp tam giác
+ Đường tròn tiếp xúc với ba cạnh của một tam giác được gọi là đường tròn nội tiếp tam giác, còn tam giác được gọi là ngoại tiếp đường tròn.
+ Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong tam giác.
8. Đường tròn bàng tiếp tam giác
+ Đường tròn tiếp xúc với một cạnh của một tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia được gọi là đường tròn bàng tiếp tam giác.
+ Với một tam giác, có ba đường tròn bàng tiếp.
+ Tâm của đường tròn bàng tiếp tam giác trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, hoặc là giao điểm của đường phân giác góc A và đường phân giác ngoài tại B (hoặc C).
9. Tính chất đường nối tâm
+ Đường nối tâm của hai đường tròn là trục đối xứng của hình gồm cả hai đường tròn đó.
+ Nếu hai đường tròn cắt nhau thi hai giao điểm đối xứng với nhau qua đường nối tâm.
+ Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
10. Vị trí tương đối của hai đường tròn
Cho hai đường tròn (O; R) và (O'; r). Đặt OO' = d.
| VTTĐ của hai đường tròn | Số điểm chung | Hệ thức giữa d với R và r |
| Hai đường tròn cắt nhau | 2 | R - r < d < R + r |
| Hai đường tròn tiếp xúc nhau: - Thiếp xúc ngoài - Tiếp xúc trong | 1 |
d = R + r d = R - r |
| Hai đường tròn không giao nhau: - Ở ngoài nhau - (O) đựng (O') | 0 |
d > R + r d < R - r |
11. Tiếp tuyến chung của hai đường tròn
+ Tiếp tuyến chung của hai đường tròn là đường thẳng tiếp xúc với cả hai đường tròn đó.
+ Tiếp tuyến chung ngoài là tiếp tuyến chung không cắt đoạn nối tâm.
+ Tiếp tuyến chung trong là tiếp tuyến chung cắt đoạn nối tâm.

B. Bài tập tự luận
Câu 1: Chứng minh rằng đường tròn ngoại tiếp tam giác vuông có tâm chính là trung điểm của cạnh huyền
Lời giải:
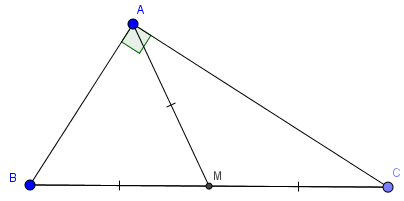
Xét tam giác ABC vuông tại A
Gọi M là trung điểm của BC nên MB = MC = 1/2 BC
Theo tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông ta có:
AM = 1/2 BC
Suy ra: MA = MB =MC = 1/2 BC
⇒ Đường tròn ngoại tiếp tam giác ABC có tâm là trung điểm của cạnh huyền
Câu 2: Cho hình chữ nhật ABCD có AB = 10, BC = 8. Chứng minh rằng A, B, C, D cùng thuộc một đường tròn và tính bán kính của đường tròn đó
Lời giải:
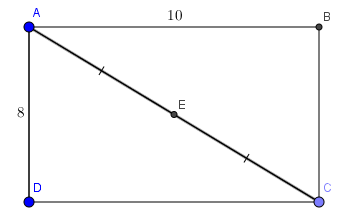
Gọi E là giao điểm của AC và BD.
Theo tính chất hình chữ nhật ta có:
EA = EB = EC = ED.
Do đó A, B, C, D cùng thuộc đường tròn tâm E và bán kính EA
Ta có: 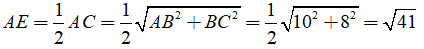
Câu 3: Cho đường tròn tâm O bán kính là 5, dây AB = 8
a) Tính khoảng cách từ O đến AB
b) Gọi I là điểm thuộc dây AB sao cho AI = 1 , kẻ dây CD đi qua I vuông góc với AB. Chứng minh rằng AB = CD
Lời giải:
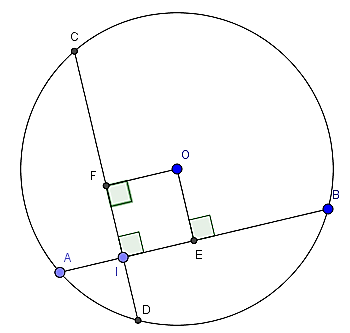
a) Gọi E là hình chiếu của O lên AB
Khoảng cách từ O đến AB chính là độ dài đoạn OE
Ta có: 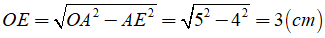
b) Gọi F là hình chiếu của O lên CD
Khi đó khoảng cách của O đến CD chính là OF
Tứ giác OFIE có ba góc vuông nên là hình chữ nhật
Do đó: OF = EI = AE - AI = 4 - 1 = 3
Suy ra OE = OF theo định lí 1 nên AB = CD
Câu 4: Cho đường tròn (O; R) . Vẽ hai đường tròn bán kính OA, OB. Trên bán kính OA, OB lấy các điểm M, N sao cho OM = ON. Vẽ dây CD đi qua MN (M giữa C và N)
a) Chứng minh: CM = DN
b) Giả sử 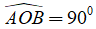
Lời giải:
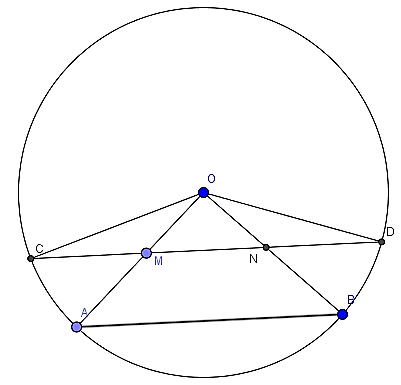
Câu 5: Cho hình thang vuông ABCD có A^=B^= 90°; BC = 2AD = 2a. Gọi H là hình chiếu vuông góc của B lên AC , M là trung điểm của HC . Tìm tâm và bán kính đường tròn ngoại tiếp tam giác BDM
Lời giải:
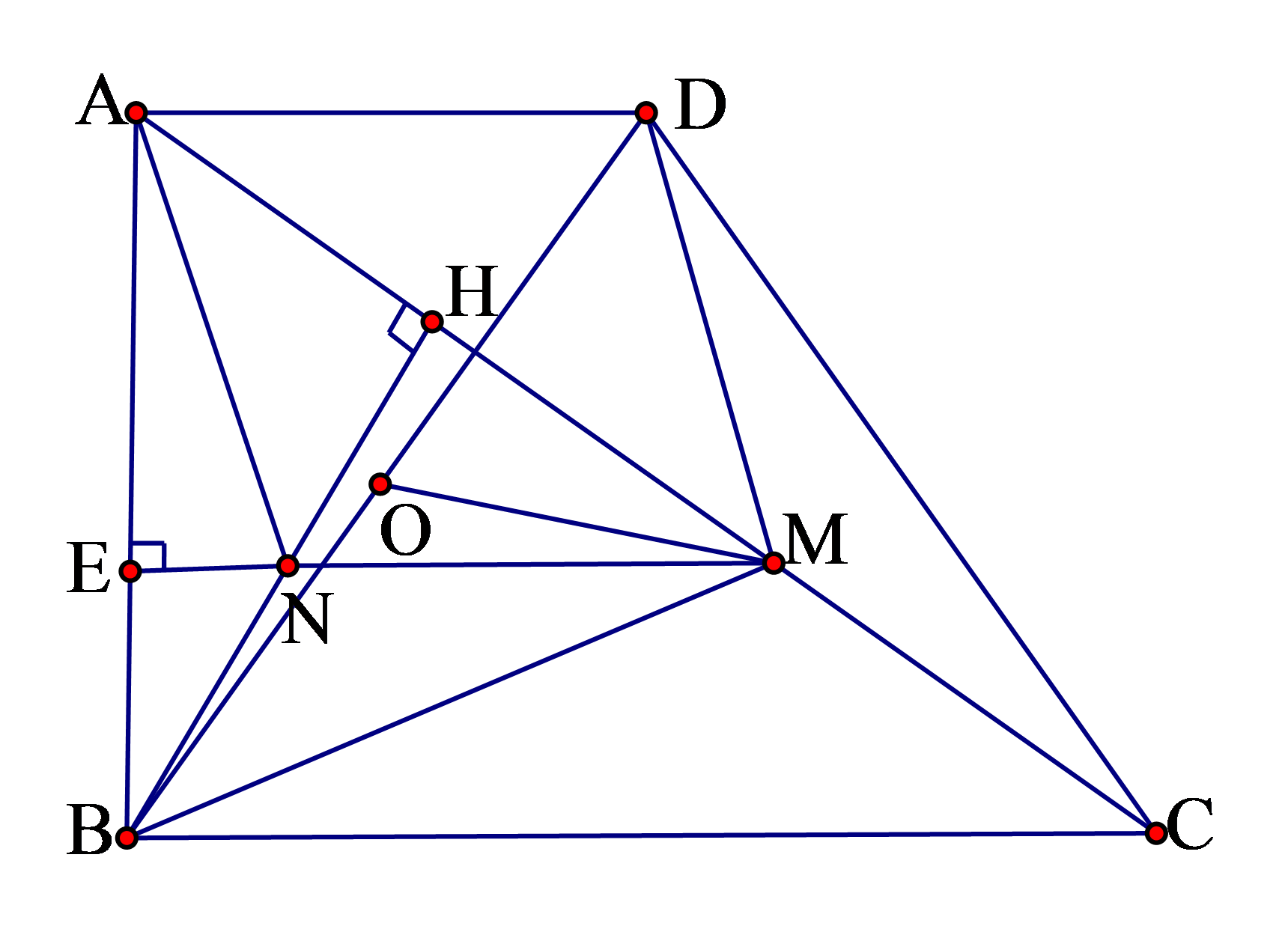
Gọi N là trung điểm của BH thì MN là đường trung bình của tam giác HBC
Suy ra MN ⊥ AB , mặt khác BH ⊥ AM ⇒
N là trực tâm của tam giác ABM
Suy ra AN ⊥ BM .
Do MN // BC; MN = 1/2 BC ⇒ MN // AD; MN = AD
Nên ADMN là hình bình hành suy ra AN // DM.
Từ đó ta có: DM ⊥ BM hay tam giác DBM vuông tại M nên tâm vòng tròn ngoại tiếp tam giác DBM là trung điểm O của BD.
Ta có:
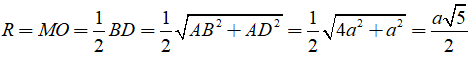

Câu 6: Cho hình thang vuông ABCD (A^=B^= 90°) có O là trung điểm của AB và góc 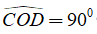
Lời giải:
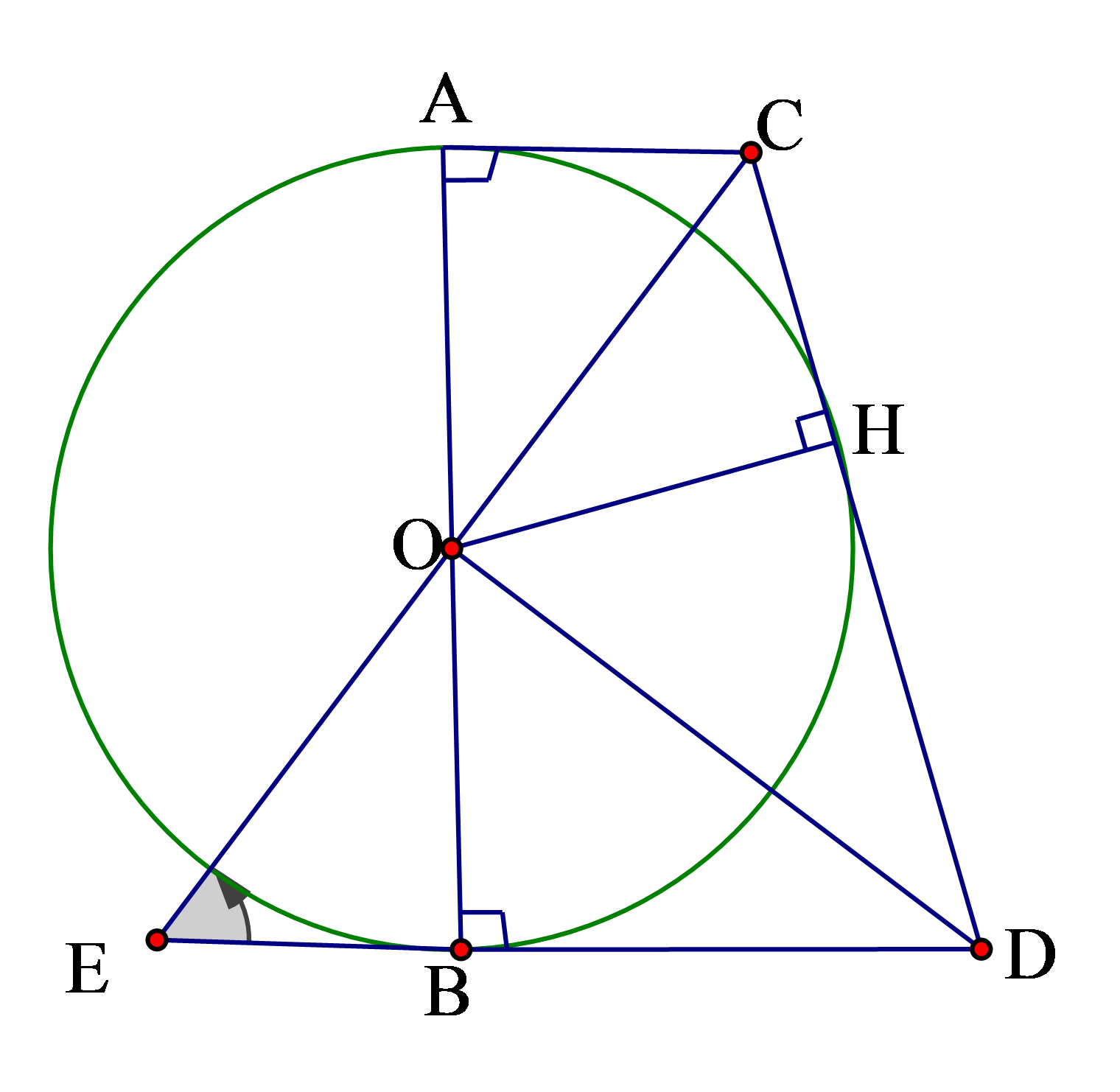
Kéo dài OC cắt BD tại E vì suy ra .

Do đó CD là tiếp tuyến của đường tròn đường kính AB.
Câu 7: Cho tam giác ABC ngoại tiếp đường tròn tâm I bán kính r. Giả sử (I; r) tiếp xúc với các cạnh AB, BC, CA lần lượt tại D, E, F . Đặt AB = c, BC = a, AC = b, AD = x, BE = y, CF = z.
a) Hãy tính x, y, z theo a, b, c
b) Chứng minh S = p.r (trong đó S là diện tích tam giác p là nữa chu vi tam giác, r là bán kính vòng tròn ngoại tiếp tam giác.
c) Chứng minh: 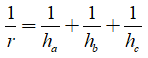
Lời giải:
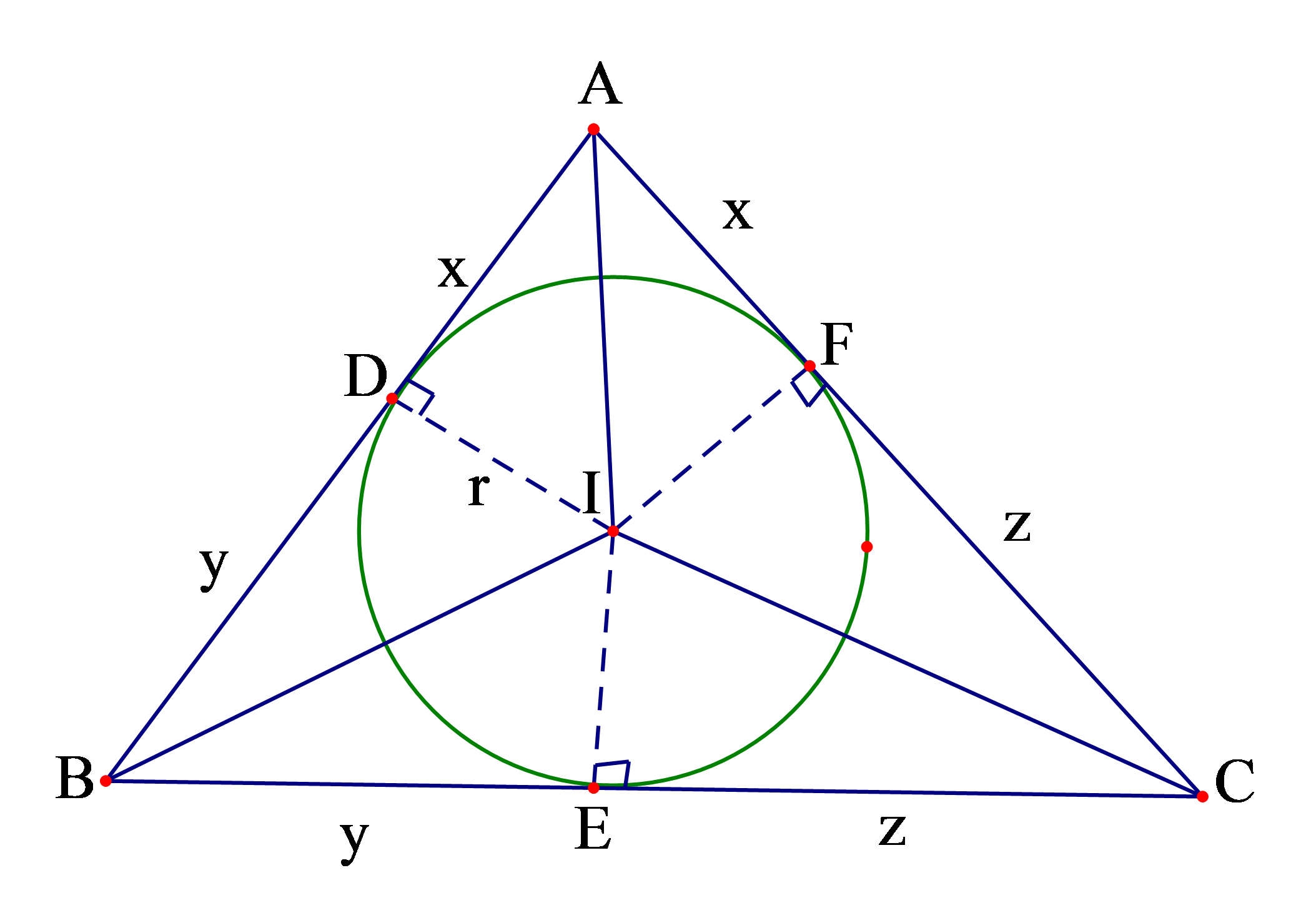
a) Từ giả thiết ta có:
AB = c, BC = a, AC = b, AD = x, BE = y, CF = z.
Từ đó suy ra
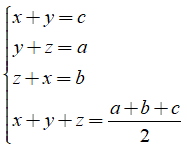
Lần lượt trừ từng vế phương trình (4) của hệ cho các phương trình ta thu được:
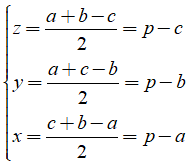
b)Ta có:
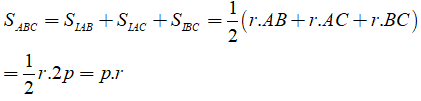
c) Ta có:
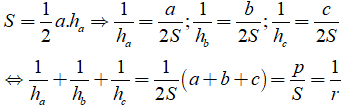
Câu 8: Cho tam giác ABC vuông tại A (AB < AC) đường cao AH. Gọi E là điểm đối xứng với B qua H. Đường tròn tâm O đường kính EC cắt AC tại K. Chứng minh HK là tiếp tuyến của đường tròn (O) .
Lời giải:
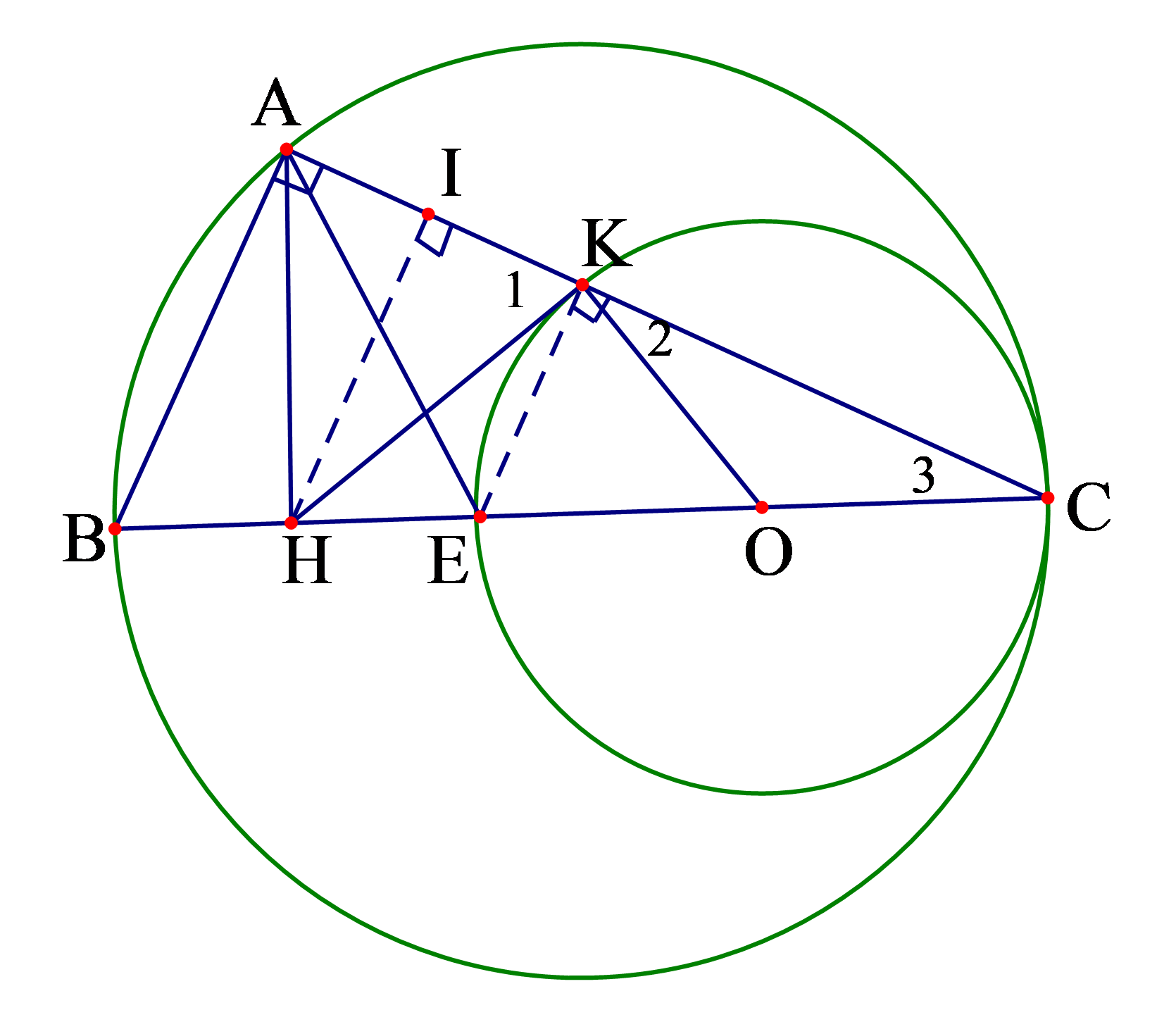
Vì tam giác EKC có một cạnh EC là đường kính của (O) nên 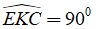
Kẻ HI ⊥ AC ⇒ BA // HI // EK .
Lại có: H là trung điểm BE
suy ra AI = IK từ đó ta có tam giác AHK cân tại H (vì có HI là đường cao đồng thời đường trung tuyến).

Câu 9: Cho tam giác ABC vuông tại A đường cao AH. Vẽ đường tròn tâm A bán kính AH kẻ các tiếp tuyến BD, CE với (A) (D, E là các tiếp điểm khác H). Chứng minh DE tiếp xúc với đường tròn đường kính BC.
Lời giải:
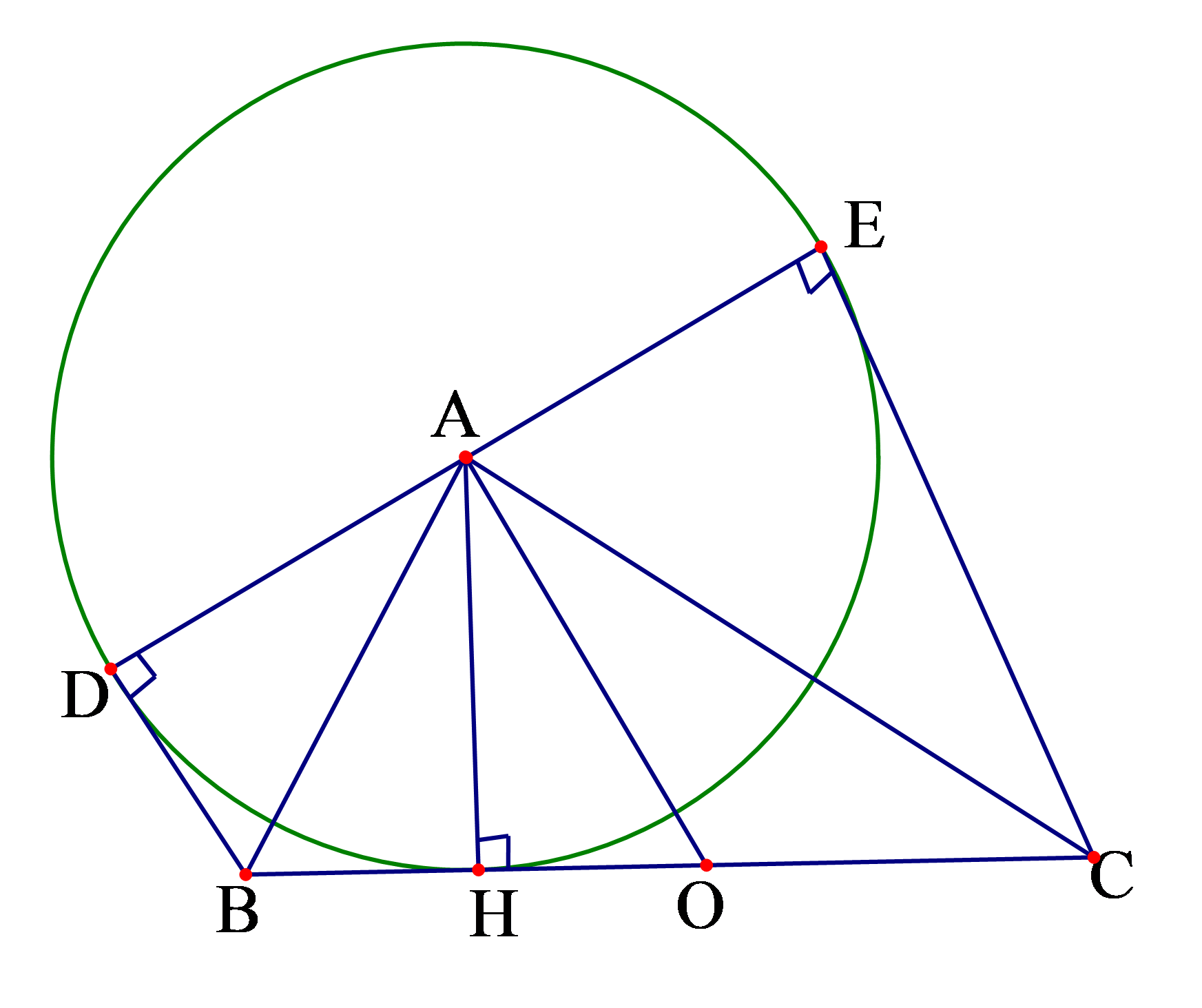
Theo tính chất của hai tiếp tuyến cắt nhau ta có: .
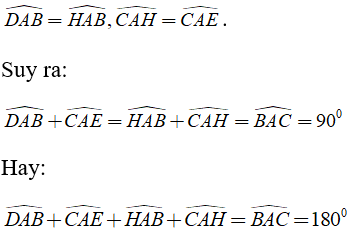
Gọi O là trung điểm của BC thì O là tâm đường tròn ngoại tiếp tam giác ABC.
Mặt khác AD = AE nên OA là đường trung bình của hình thang vuông BDEC suy ra OA ⊥ DE tại A.
Nói cách khác DE là tiếp tuyến của đường tròn (O).
Do đó DE tiếp xúc với đường tròn đường kính BC.
Câu 10: Cho nửa đường tròn tâm O đường kính AB. Vẽ các tia Ax vuông góc với AB, By vuông góc với AB ở cùng phía với nửa đường tròn. I là một điểm thuộc trên nửa đường tròn. Tiếp tuyết tại I cắt Ax, By tại C và D.
a) CMR: Tam giác COD là tam giác vuông
b) Tìm vị trí điểm I để chu vi tứ giác ACDB là nhỏ nhất. Tính chu vi theo R.
Lời giải:
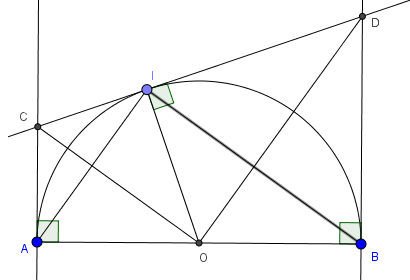
a) Ta có tam giác IAB vuông tại I
Gọi E là giao điểm của AI và CO, F là giao điểm của IB và OD

b) Vì tiếp tuyến tại A và I cắt nhau tại C nên CA = CI
Tương tự: DB = DI
Khi đó: AC + BD = IC + ID = CD
Ta lại có: CD ≥ AB vì AB là đoạn vuông góc với hai đường thẳng song song là AC và BD
Khi đó: Chu vi tứ giác ACDB là:
AC + BD + CD + AB = 2CD + AB ≥ 3AB = 3R
Câu 11: Cho tam giác ABC cân tại A nội tiếp đường tròn (O) . Các tiếp tuyến của (O) vẽ từ A và C cắt nhau tại M. Trên tia AM lấy điểm D sao cho AD = BC . Chứng minh: AC, BD, OM đồng quy
Lời giải:
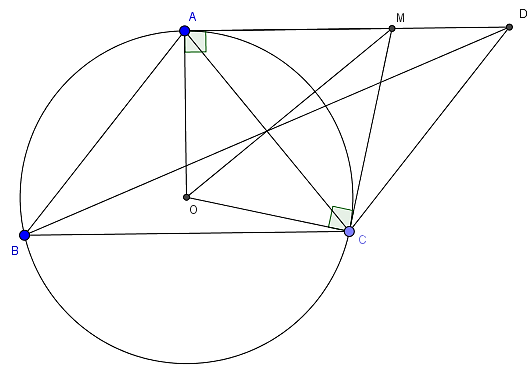
Trước tiên, ta chứng minh ABCD là hình bình hành
Ta có AO vuông góc với BC, AO vuông góc với AD nên AD // BC
Mà AD = BC ⇒ ABCD là hình bình hành
Gọi E là giao điểm của AC và OM
Theo tính chất của hai tiếp tuyến cắt nhau thì E là trung điểm của AC (do tam giác MAC cân tại M, có ME là đường cao)
Do ABCD là hình bình hành nên đường chéo sẽ đi qua trung điểm của mỗi đường
Nên BD đi qua điểm E
Do đó AC, BD, OM đồng quy tại E


