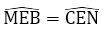Bài tập về đường tròn chọn lọc, có lời giải | Toán lớp 9

Bài tập về đường tròn chọn lọc, có lời giải

Với Bài tập về đường tròn chọn lọc, có lời giải Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Bài 1: Cho một đường tròn (O) và một điểm M nằm ngoài (O). Tia MO cắt (O) tại A, B (A nằm giữa M và O. Chứng minh rằng:

    a) MA là khoảng cách nhỏ nhất từ M tới các điểm của (O)

    b) MB là khoảng cách lớn nhất từ M tới các điểm của (O)

Bài 2: Cho đường tròn (O) đường kính AD = 2R; gọi I là trung điểm của OD. Qua I kẻ dây BC vuông góc với AD

    a) Chứng minh tam giác ABC là tam giác đều

    b) Tính độ dài các cạnh của tam giác ABC theo R

Bài 3: Cho tam giác ABC cân tại A, các đường cao AD và BE cắt nhau tại H. Gọi M và N lần lượt là trung điểm của AB và CH. Chứng minh rằng:

    a) MD ⊥ BE

    b) Bốn điểm M, N, D, E cùng nằm trên một đường tròn.

Bài 4: Cho đường tròn (O; 5cm). Hai dây AB và CD song song với nhau. Tính khoảng cách giữa AB và CD biết AB = 6cm, CD = 8cm.

Bài 5: Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi H là giao điểm của đường trung tuyến CM với OA. Gọi G là trọng tâm của tam giác AMC. Chứng minh rằng:

    a) OM ⊥ GH

    b) OG ⊥ CM

Bài 6: Cho đường tròn (O; R) và một điểm A cố định trên đường tròn, B là một điểm di động trên đường tròn. Gọi M là một điểm trên AB sao cho 3AM = 2AB. Chứng minh rằng khi điểm B di động trên đường tròn (O) thì điểm M di động trên một đường tròn cố định.

Bài 7: Cho đường tròn (O) đường kính AB; C là điểm di động trên đường tròn; H là hình chiếu của C trên AB. Trên OC lấy điểm M sao cho OM = OH

    a) Điểm M chạy trên đường nào?

    b) Kéo dài BC một đoạn CD = CB. Điểm D chạy trên đường nào?

Đáp án và hướng dẫn giải

Bài 1:

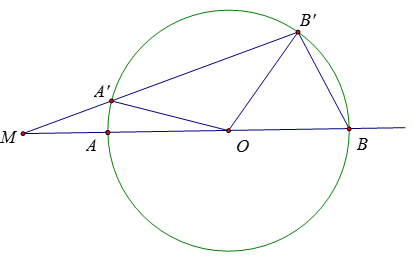
    Từ M kẻ cát tuyến bất kì cắt (O) tại A’, B’. Gọi bán kính của (O) là R.

    a) Trong ΔMA’O có:

    MO < OA’ + MA’ (Theo bất đẳng thức tam giác)

    ⇔ MA + AO < MA' + OA'

    ⇔ MA + R < MA' + R

    ⇔ MA < MA'

    Do kẻ cát tuyến MA’B’ bất kì, mà MA < MA’ nên MA là khoảng cách nhỏ nhất từ M tới (O).

    b) ΔOBB' cân tại O

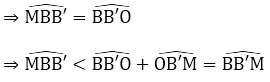
    Xét tam giác MBB’ có:

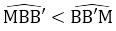
    ⇒ MB' < MB (góc đối diện với cạnh lớn hơn thì lớn hơn và ngược lại)

    Do kẻ cát tuyến MA’B’ bất kì, mà MB’ < MB nên MB là khoảng cách lớn nhất từ M tới (O).

Bài 2:

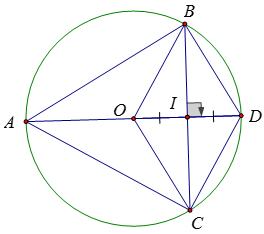
    a) Đường kính AD vuông góc với dây BC tại I nên I là trung điểm của dây BC

    Tứ giác OBDC có:

    I là trung điểm của BC và OD

    OD ⊥ BC

    ⇒ Tứ giác OBDC là hình thoi

    ⇒ BD = OB = R

    Mặt khác: do ΔABD có OA = OB = OD = R nên ΔABD vuông tại B.

    ΔABD có cạnh góc vuông BD = 1/2 AD ⇒ góc BAD bằng 30⁰

    ΔABC có AI ⊥ BC và IB = IC ⇒ ΔABC cân tại A

    ⇒ AI cũng đồng thời là đường phân giác của góc A

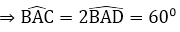
    ΔABC cân có một góc bằng 60⁰

    ⇒ ΔABC đều

    b) Trong ΔABD vuông tại D có:

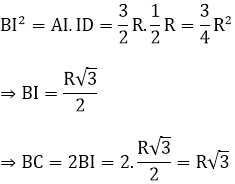
Bài 3:

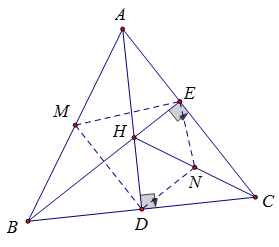
    a) Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông

    Trong tam giác AED vuông tại E có EM là trung tuyến

    ⇒ MB = ME = AB/2

    Trong tam giác BEC vuông tại E có ED là trung tuyến

    ⇒ BD = DE = BC/2

    ⇒ MD là đường trung trực của BE, do đó MD ⊥ BE

    b) Ta có DN là đường trung bình của tam giác BHC nên DN // BE

    ⇒ MD ⊥ DN, góc MDN bằng 90⁰

    Vì H là trực tâm của tam giác ABC nên CH⊥ AB

    Do đó: 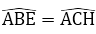(cùng phụ với góc BAC )(1)

    ΔMBE cân nên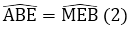

    ΔNCE cân nên 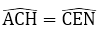(3)

    Từ (1), (2) và (3) suy ra

    Ta có:

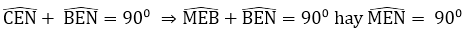
    Hai tam giác vuông MDN và MEN chung cạnh huyền MN nên bốn điểm M, N, D, E cùng nằm trên một đường tròn có đường kính là MN

Bài 4:

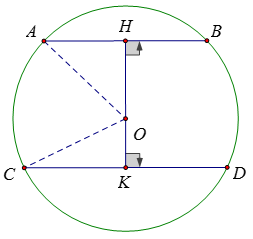
    Vẽ OH ⊥ AB; OK ⊥ CD

    Do AB // CD nên 3 điểm H, O, K thẳng hàng

    AH = 3cm; CK = 4 cm; R = 5 cm

    Áp dụng định lí Pytago vào các tam giác vuông AHO, CKO ta được:

    OH = 4 cm; OK = 3 cm

    * Nếu O nằm giữa H và K thì HK = 7 cm

    * Nếu O không nằm giữa H và K thì HK = 1 cm

Bài 5:

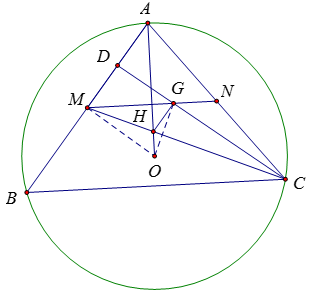
    a) Gọi D là giao điểm của CG với AB, N là giao điểm của MG với AC

    Ta có H là trọng tâm của tam giác ABC; G là trọng tâm của tam giác AMC

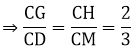
    ⇒ AB // GH

    Mặt khác OM ⊥ AB (tính chất đường kính và dây cung)

    ⇒ OM ⊥ GH

    b) Ta có: MN là đường trung bình của tam giác ABC nên MN // BC

    mà OA ⊥ BC nên OA ⊥ MN

    Xét tam giác OMG có H là giao điểm của hai đường cao nên MH là đường cao thứ ba, do đó MH ⊥ OG hay OG ⊥ CM

Bài 6:

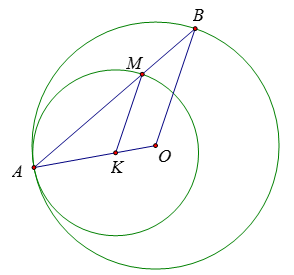
    Gọi K là điểm trên bán kính OA sao cho 3AK = 2AO

    Do A, O cố định nên K cố định

    Xét ΔAMK và ΔABO có:

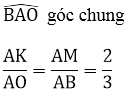
    ⇒ ΔAMK ~ ΔABO (c.g.c)

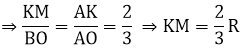
    Do đó, M ∈ (K; 2/3R)

Bài 7:

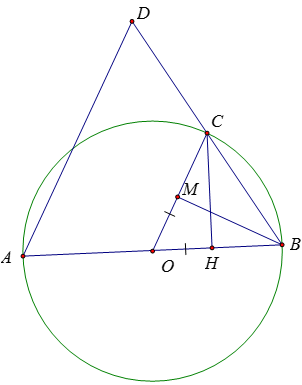
    a) Xét ΔOMB và ΔOHC có:

    OM = OH

    góc O chung

    OB = OC

    ⇒ ΔOMB = ΔOHC (c.g.c)

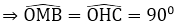
    Vậy M chạy trên đường tròn đường kính OB

    b) Vì C ∈ (O) ⇒ góc ACB bằng 90⁰ hay AC ⊥ DB

    Mà CD = CB ⇒ Tam giác ADB có AC vừa là đường cao vừa là trung tuyến nên ΔABD cân tại A

    ⇒ AD = AB = 2R

    Vậy D chạy trên đường tròn (A; 2R)