Lý thuyết Liên hệ giữa dây và khoảng cách từ tâm đến dây hay, chi tiết | Toán lớp 9
Lý thuyết Liên hệ giữa dây và khoảng cách từ tâm đến dây hay, chi tiết
Tài liệu Lý thuyết Liên hệ giữa dây và khoảng cách từ tâm đến dây hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Liên hệ giữa dây và khoảng cách từ tâm đến dây từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Định lý 1
Trong một đường tròn:
a) Hai dây bằng nhau thì cách đều tâm.
b) Hai dây cách đều tâm thì bằng nhau.
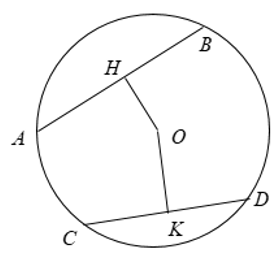
Áp dụng vào hình vẽ như sau:
Ta có OH ⊥ AB; OK ⊥ CD.
AB = CD ⇔ OH = OK
2. Định lý 2

Trong hai dây của một đường tròn:
a) Dây nào lớn hơn thì dây đó gần tâm hơn.
b) Dây nào gần tâm hơn thì dây đó lớn hơn.
Áp dụng vào hình vẽ như sau:
Ta có: OA = OB = OC = OD = R
OH < OK ⇒ AB > CD
Do
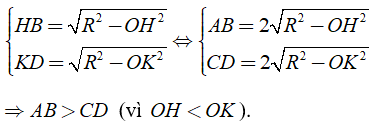

3. Ví dụ cụ thể
Câu 1: Cho đường tròn tâm O có bán kính là 5cm, dây AB dài 8cm.
a) Tính khoảng cách từ tâm O đến dây AB.
b) Gọi I là điểm thuộc dây AB sao cho AI = 1cm. Kẻ dây CD qua I vuông góc với AB. Chứng minh rằng CD = AB
Hướng dẫn:
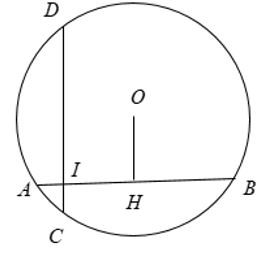
a) Gọi H là trung điểm của AB.
AH = HB = AB/2 = 4 cm
⇒ OH ⊥ AB.
Khi đó:
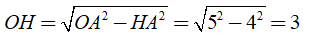
b)Điểm I nằm giữa A và H nên: AI + IH = AH
suy ra: IH = AH – AI = 4 - 1= 3 cm
Từ O kẻ OK ⊥ CD.
Ta có OKIH là hình chữ nhật mà có OH = IH = 3cm ⇒ OKIH là hình vuông
Nhận xét: Khoảng cách từ O đến AB bằng khoảng cách từ O đến CD nên
Giải thích:
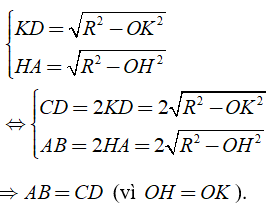

B. Bài tập tự luận
Câu 1: Cho đường tròn tâm O bán kính là 5, dây AB = 8
a) Tính khoảng cách từ O đến AB
b) Gọi I là điểm thuộc dây AB sao cho AI = 1 , kẻ dây CD đi qua I vuông góc với AB. Chứng minh rằng AB = CD
Lời giải:
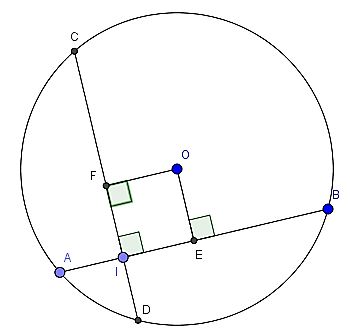
a) Gọi E là hình chiếu của O lên AB
Khoảng cách từ O đến AB chính là độ dài đoạn OE
Ta có: 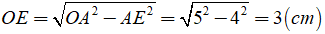
b) Gọi F là hình chiếu của O lên CD
Khi đó khoảng cách của O đến CD chính là OF
Tứ giác OFIE có ba góc vuông nên là hình chữ nhật
Do đó: OF = EI = AE - AI = 4 - 1 = 3
Suy ra OE = OF theo định lí 1 nên AB = CD
Câu 2: Cho đường tròn (O; R) . Lấy các điểm A và B trên đường tròn. Trên bán kính OA, OB lấy các điểm M, N sao cho OM = ON . Vẽ dây CD đi qua MN; M giữa C và N
a) Chứng minh: CM = DN
b) Giả sử 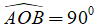
Lời giải:
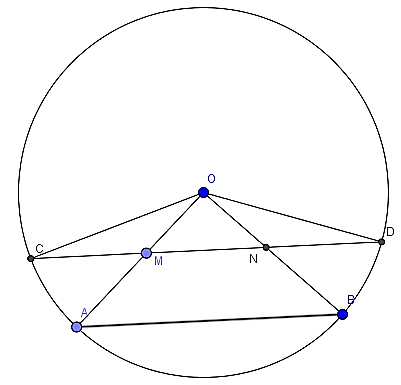
a) Xét hai tam giác COM và DON có:
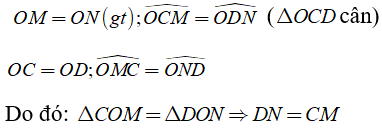
b) Gọi H là hình chiếu vuông góc của O lên MN


