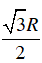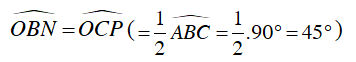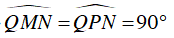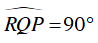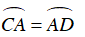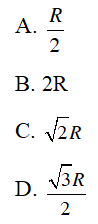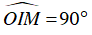Cách chứng minh nhiều điểm cùng thuộc một đường tròn cực hay | Toán lớp 9

---

Cách chứng minh nhiều điểm cùng thuộc một đường tròn cực hay

Với Cách chứng minh nhiều điểm cùng thuộc một đường tròn cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập chứng minh nhiều điểm cùng thuộc một đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

+ Chứng minh các điểm cùng cách đều một điểm O một khoảng bằng R. Khi đó các điểm đó sẽ thuộc đường tròn tâm O, bán kính R.

+ Sử dụng cung chứa góc: Chứng minh các điểm liên tiếp cùng nhìn một đoạn AB cố định dưới một góc α bằng nhau. Hay chính là các điểm đó cùng thuộc một cung chứa góc α dựng trên đoạn AB, nên các điểm đó cùng thuộc một đường tròn chứa cung chứa góc α dựng trên đoạn AB.

B. Ví dụ minh họa

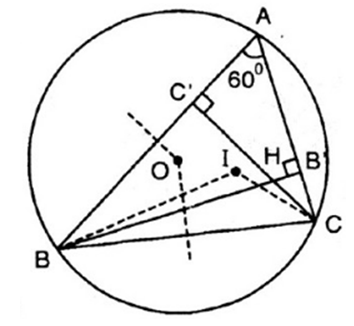
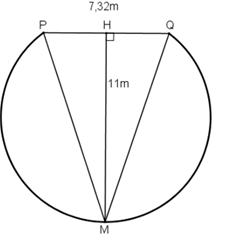
Ví dụ 1 : Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp tam giác ABC với A = 60^o. Gọi H là giao điểm của các đường cao BB' và CC'. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn.

Hướng dẫn giải

+ Xét trên đường tròn (O):

là góc ở tâm chắn cung BC

là góc nội tiếp chắn cung BC

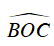
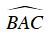
+ Tứ giác AC’HB’ có:

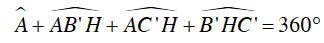
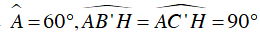
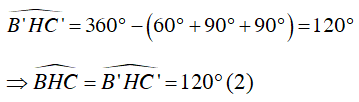
Mà ( BB’, CC’ là các đường cao)

+ Do I là tâm đường tròn nội tiếp tam giác ABC

Suy ra BI, CI lần lượt là các tia phân giác của .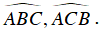

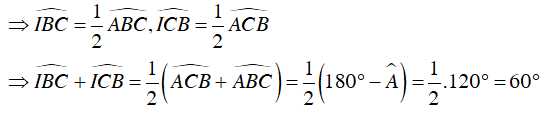
Xét tam giác IBC, ta có: 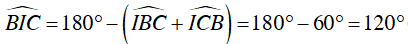(3)

Từ (1), (2) và (3)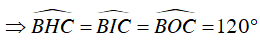

Do đó, H, I và O cùng nhìn BC cố định dưới một góc 120^o.

Suy ra, H, I và O thuộc cung chứa góc 120^o dựng trên đoạn BC.

⇒ B, O, I, H, C cùng thuộc đường tròn chứa cung 120^o dựng trên đoạn BC.

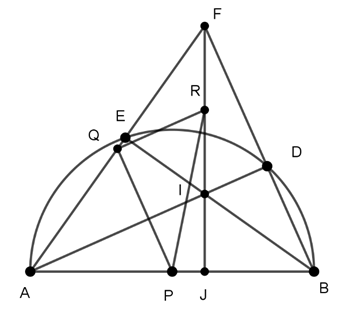
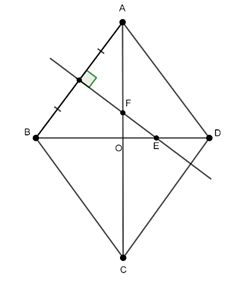
Ví dụ 2 : Cho nửa đường tròn đường kính AB trên đó lấy hai điểm D và E ( E nằm giữa A và D). AD cắt BE tại I, AE cắt BD tại F.

a. Chứng minh IF ⊥ AB tại J

b. Gọi P, Q, R lần lượt là trung điểm của AB, AF, IF. Chứng minh 4 điểm J, P, Q, R cùng nằm trên một đường tròn.

Hướng dẫn giải

a. Ta có D, E thuộc đường tròn đường kính AB

⇒ ( góc nội tiếp chắn nửa đường tròn)

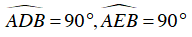
⇒ AD, BE là đường cao của tam giác AFB

Mà BE giao AD tại I

⇒ I là trực tâm của tam giác AFB

⇒ IF là đường cao của tam giác AFB

⇒ IF ⊥ AB tại J (đpcm)

b. ΔPJR vuông tại J (IJ ⊥ AB) ⇒ 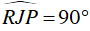⇒ J nằm trên đường tròn đường kính PR (*)

P, Q là trung điểm của AB và BF ⇒ PQ là đường trung bình của ΔABF

⇒ PQ // BF

Mà AD BF

⇒ AD ⊥ PQ

R, Q là trung điểm IF và BF ⇒ RQ là đường trung bình của ΔIFA

⇒ RQ // AD

Mà AD ⊥ PQ

⇒ RQ ⊥ PQ

⇒

⇒ Q nằm trên đường tròn đường kính PR (**)

Từ (*) và (**) suy ra bốn điểm P, Q, R, J cùng nằm trên đường tròn đường kính PR.

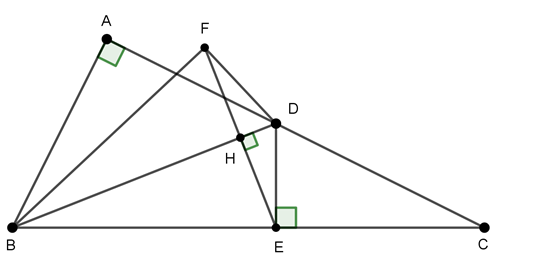
Ví dụ 3 : Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó.

Hướng dẫn giải

ΔBAD có góc A bằng 90^o A nằm trên đường tròn đường kính BD.

ΔBED có góc E bằng 90^o (E là hình chiếu của D lên BC) ⇒ E nằm trên đường tròn đường kính BD.

F đối xứng với E qua BD nên F cũng nằm trên đường tròn đường kính BD (tính chất đối xứng của đường tròn).

Vây 5 điểm A, B, E, D, F cùng nằm trên đường tròn đường kính BD tâm O là trung điểm của BD.

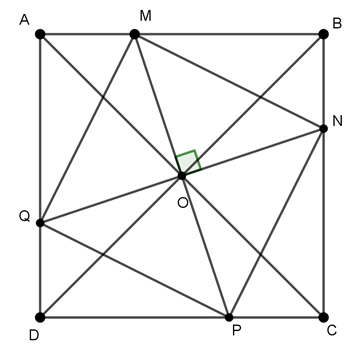
Ví dụ 4 : Cho hình vuông ABCD, hai đường chéo cắt nhau tại O. Qua O vẽ hai đường thẳng vuông góc với nhau cắt các cạnh AB, BC, CD, DA lần ượt tại M, N, P, Q. Chứng minh 4 điểm M, N, P, Q cùng thuộc một đường tròn.

Hướng dẫn giải

+ Xét ΔAMO và ΔCPO , ta có:

(hai góc so le trong)

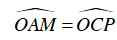
OA = OC (tính chất hình vuông)

(hai góc đối đỉnh)

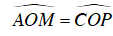
⇒ ΔAMO = ΔCPO (g – c – g)

⇒ OM = OP (hai cạnh tương ứng) (1)

+ Chứng minh tương tự với cặp ΔBNO và ΔDQO

⇒ ON = OQ (hai cạnh tương ứng) (2)

+ Xét ΔBNO và ΔCPO , ta có:

OB = OC (tính chất hình vuông)

(hai góc cùng phụ với )

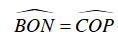
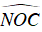
⇒ ΔBNO = ΔCPO (g – c – g)

⇒ ON = OP (3)

+ Tứ giác MNPQ, có OM = OP, ON = OQ

⇒ MNPQ là hình bình hành ( theo dấu hiệu nhận biết)

Từ (1), (2) và (3) suy ra: MP = QN

⇒ MNPQ là hình chữ nhật

⇒

Do đó M và P cùng thuộc đường tròn đường kính QN

Vậy M, N, P, Q cùng thuộc một đường tròn đường kính QN.

Ví dụ 5 : "Góc sút" của quả phạt đền 11 mét là bao nhiêu độ? Biết rằng chiều rộng cầu môn là 7,32m. Hãy chỉ ra hai vị trí khác trên sân có cùng "góc sút" như quả phạt đền 11 mét.

Hướng dẫn giải

Gọi vị trí đặt quả bóng để sút phạt đền là M, và bề ngang cầu môn là PQ thì M nằm trên đường trung trực của PQ.

Gọi H là trung điểm của PQ, ta có: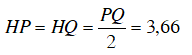

Gọi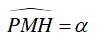

Do M nằm trên đường trung trực của PQ nên MH vuông góc PQ.

Tam giác MPH vuông tại H, áp dụng tỉ số lượng giác trong tam giác vuông ta có:

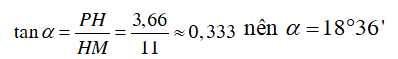
Vậy góc sút phạt đền là 2α ≈ 37^o12’

+ Vẽ cung chứa góc 37^o12’ dựng trên đoạn thẳng PQ. Bất cứ điểm nào trên cung vừa vẽ cũng có cùng “góc sút” như quả phạt đền 11m.

C. Bài tập trắc nghiệm

Câu 1 : Cho tam giác ABC cân tại A, các đường cao AI, BK, CL cắt nhau tại H. Khi đó:

a. Bốn điểm A, B, K, H nằm trên một đường tròn

b. Bốn điểm B, L, K, H nằm trên một đường tròn

c. Bốn điểm B, C, K, L nằm trên một đường tròn

d. Bốn điểm A, C, L, H nằm trên một đường tròn

Hướng dẫn giải

Đáp án C

+ B, H, K cùng nằm trên một đường thẳng nên bốn điểm A, B, K, H không cùng nằm trên một đường tròn; bốn điểm B, L, K, H cùng không cùng nằm trên một đường tròn.

+ C, L, H cùng nằm trên một đường thẳng nên bốn điểm A, C, L, H không cùng nằm trên một đường tròn.

+ Ta có: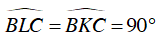

Suy ra K, L cùng thuộc đường tròn đường kính BC, nên bốn điểm B, C, L, K cùng nằm trên một đường tròn.

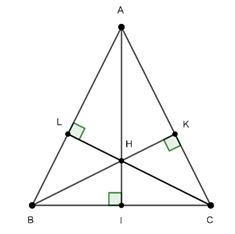
Câu 2 : Cho nửa đường tròn đường kính AB trên đó lấy hai điểm D và E (D nằm giữa A và E). AD cắt BE tại I, AE cắt BD tại F, IF cắt AB tại J. Gọi P, Q, R, M và N lần lượt là trung điểm của AB, BF, IF, BI và IA. Khi đó 8 điểm Q, R, E, N, J, P, M , D cùng nằm trên đường tròn:

A. đường kính PR

B. đường kính DQ

C. đường kính SE

D. đường kính JR

Hướng dẫn giải

Đáp án A

+ Ta có: Ta có D, E thuộc đường tròn đường kính AB

⇒ ( góc nội tiếp chắn nửa đường tròn)

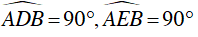
⇒ AD, BE là đường cao của tam giác AFB

Mà BE giao AD tại I

⇒ I là trực tâm của tam giác AFB

⇒ IF là đường cao của tam giác AFB

⇒ IF ⊥ AB tại J (đpcm)

+ ΔPJR vuông tại J (IJ ⊥ AB) ⇒ 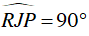⇒ J nằm trên đường tròn đường kính PR (*)

P, Q là trung điểm của AB và BF ⇒ PQ là đường trung bình của ΔABF

⇒ PQ // BF

Mà AD ⊥ BF

⇒ AD ⊥ PQ

R, Q là trung điểm IF và BF ⇒ RQ là đường trung bình của ΔIFA

⇒ RQ // AD

Mà AD ⊥ PQ

⇒ RQ ⊥ PQ

⇒

⇒ Q nằm trên đường tròn đường kính PR (**)

Từ (*) và (**) suy ra bốn điểm P, Q, R, J cùng nằm trên đường tròn đường kính PR.

Mà 8 điểm Q, R, E, N, J, P, M , D cùng nằm trên đường tròn

Suy ra 8 điểm Q, R, E, N, J, P, M , D cùng nằm trên đường tròn đường kính PR.

Câu 3 : Cho hình thoi ABCD, đường trung trực của cạnh AB cắt BD tại E và cắt AC tại F. Khi đó.

A. E là tâm của đường tròn ngoại tiếp tam giác ABD

B. F là tâm của đường tròn ngoại tiếp tam giác ABD

C. E là tâm của đường tròn ngoại tiếp tam giác BCD

D. F là tâm của đường tròn ngoại tiếp tam giác ABC

Hướng dẫn giải

Đáp án B

Vì ABCD là hình thoi

⇒ AC ⊥ BC , O là trung điểm của BD

Hay AC là đường trung trực của BD

Xét tam giác ABD, hai đường trung trực cắt nhau tại F

Do đó, F là tâm đường tròn ngoại tiếp tam giác ABD.

Câu 4 : Cho nửa đường tròn đường kính AB trên đó lấy hai điểm D và E ( D nằm giữa A và E). AD cắt BE tại I, AE cắt BD tại F, FI cắt AB tại J. Chọn phát biểu sai.

A. I, D, E, F cùng thuộc một đường tròn

B. I, D, B, J cùng thuộc một đường tròn

C. I, J, E, A cùng thuộc một đường tròn

D. I, J, F, D cùng thuộc một đường tròn

Hướng dẫn giải

Đáp án D

Vì I, J, F nằm trên cùng một đường thẳng nên bốn điểm I, J, F, D không cùng thuộc một đường tròn.

Câu 5 : Cho hình chữ nhật ABCD có AB = 8cm, BC = 6cm. Độ dài bán kính của đường tròn đi qua 4 điểm A, B, C, D bằng:

A. 5cm

B. 8cm

C. 6cm

D. 10cm

Hướng dẫn giải

Đáp án A

Vì ABCD là hình chữ nhật nên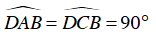

⇒ A, C cùng thuộc đường tròn đường kính BD

⇒ A, B, C, D cùng thuộc đường tròn đường kính BD

Gọi O là trung điểm của BC.

Xét tam giác ABD vuông tại A, ta có:

BD² = AB² + BD² = 8² + 6² = 100

⇒ DB = 10cm

⇒ .

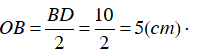
Vậy bán kính đường tròn đi qua 4 điểm là 5 cm.

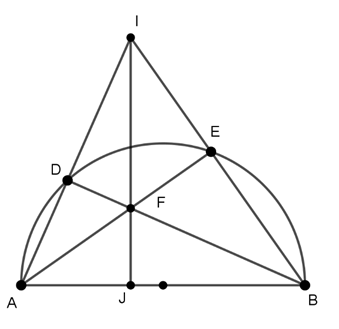
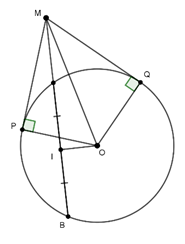
Câu 6 : Từ điểm M nằm bên ngoài đường tròn (O), kẻ cát tuyến MAB đi qua O và các tiếp tuyến MC, MD. Gọi K là giao điểm của AC và BD. Bốn điểm nào sau đây cùng thuộc một đường tròn

A. B, C, M, K thuộc cùng một đường tròn.

B. D, M, A, B cùng thuộc một đường tròn.

C. M, A, O, B cùng thuộc một đường tròn.

D. D, M, C, A cùng thuộc một đường tròn.

Hướng dẫn giải

Đáp án A

Ta có tiếp tuyến tại C cắt tiếp tuyến tại D tại M. Khi đó:

MC = MD (tính chất hai tiếp tuyến cắt nhau)

⇒ M thuộc vào trung trực của CD

OC = OD = R

⇒ O thuộc vào trung trực của CD

Do đó, MO là đường trung trực của CD hay AB là đường trung trực của CD.

⇒

Suy ra 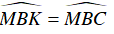(hai góc nội tiếp chắn hai cung bằng nhau)

Mặt khác 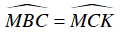(góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung CA)

Do đó :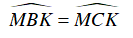

⇒ Hai đỉnh liên tiếp B, C cùng nhin cạnh MK dưới góc bằng nhau

Nên B,C thuộc cùng một cung chứa góc dựng trên đoạn MK nên M, C, B, K cùng thuộc một đường tròn .

Câu 7 : Cho tam giác ABC vuông tại A. Qua C kẻ đường thẳng vuông góc với phân giác trong góc 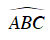tại D. Bốn điểm A, B, C, D cùng nằm trên đường tròn có tâm là:

A. M trung điểm của AB

B. N là trung điểm của BD

C. P là trung điểm của AC

D. Q là trung điểm của BC

Hướng dẫn giải

Đáp án D

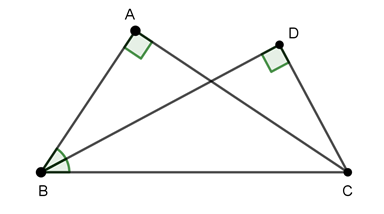
Ta có :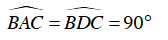

⇒ A, D cùng thuộc đường tròn đường kính BC

Do đó bốn điểm A, B, C, D cùng thuộc một đường tròn có tâm là trung điểm của BC.

Câu 8 : Lấy một điểm M nằm ngoài một đường tròn (O;R) sao cho 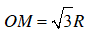. Từ M kẻ hai tia tiếp tuyến MQ, MP ( P, Q là các tiếp điểm ) và một cát tuyến MAB ( A nằm giữa M và B). Gọi I là trung điểm của AB. Bán kính đường tròn đi qua 5 điểm M, P, I, O, Q là:

Hướng dẫn giải

Đáp án D

Ta có I là trung điểm của AB

⇒ OI ⊥ AB tại I

⇒

Ta lại có : 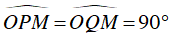( MP, MQ là tiếp tuyến của (O))

⇒

Suy ra P, Q, I cùng thuộc đường tròn đường kính OM, có tâm là trung điểm của OM

Do đó 5 điểm P, Q, I, O, M cùng thuộc đường tròn đường kính OM, có bán kính bằng .