Các dạng bài tập Phương trình quy về phương trình bậc hai cực hay, có đáp án | Toán lớp 9

Các dạng bài tập Phương trình quy về phương trình bậc hai cực hay, có đáp án

Với Các dạng bài tập Phương trình quy về phương trình bậc hai cực hay, có đáp án Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Phương trình quy về phương trình bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Giải phương trình trùng phương: Cho phương trình ax⁴ + bx² + c = 0 (a ≠ 0) (1)

Bước 1: Đặt x² = t (ĐK t ≥ 0), ta được phương trình bậc hai ẩn t: at² + bt + c = 0 (a ≠ 0) (2)

Bước 2: Giải phương trình bậc hai ẩn t.

Bước 3: Giải phương trình x² = t để tìm nghiệm .

Bước 4: Kết luận.

Biện luận số nghiệm của phương trình trùng phương

+) Phương trình (1) có 4 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm dương phân biệt.

+) Phương trình (1) có 3 nghiệm phân biệt ⇒ phương trình (2) có 1 nghiệm dương và một nghiệm t = 0.

+) Phương trình (1) có 2 nghiệm phân biệt ⇒ phương trình (2) có 2 nghiệm trái dấu hoặc có nghiệm kép dương.

+) Phương trình (1) có duy nhất 1 nghiệm ⇒ phương trình (2) có nghiệm kép x = 0 hoặc có một nghiệm x = 0 và một nghiệm âm.

+) Phương trình (1) vô nghiệm ⇒ phương trình (2) vô nghiệm hoặc có hai nghiệm âm.

Giải phương trình chứa ẩn ở mẫu

Bước 1: Tìm điều kiện xác định.

Bước 2: Quy đồng, khử mẫu, rút gọn đưa về dạng phương trình bậc hai.

Bước 3: Giải phương trình bậc hai.

Bước 4: So sánh với điều kiện và kết luận.

Giải phương trình tích: Cho phương trình A(x).B(x)...C(x) = 0 (1), trong đó A(x).B(x)...C(x) là các phương trình ẩn x.

Bước 1: Biến đổi tương đương A(x).B(x)...C(x) = 0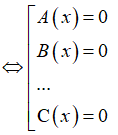

Bước 2: Lần lượt giải các phương trình A(x) = 0; B(x) = 0;... C(x) = 0.

Bước 3: Kết luận.

B. Các ví dụ điển hình

Ví dụ 1: Số nghiệm của phương trình x⁴ - 6x² + 8 = 0 là:

Lời giải

Chọn D

Ví dụ 2: Phương trình x⁴ + 2(m + 1)x² + m² = 0 vô nghiệm khi:

Lời giải

Chọn B

Ví dụ 3: Cho phương trình x⁴ - 2(m + 1)x² + 2m + 3 = 0 là tham số. Tìm số tự nhiên m nhỏ nhất để phương trình có bốn nghiệm phân biệt.

Lời giải

Chọn A

Ví dụ 4: Giải phương trình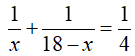

Lời giải

Chọn A

Ví dụ 5: Cho phương trình . Chọn khẳng định đúng về nghiệm của phương trình: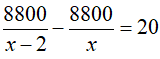

Lời giải

Chọn D

Ví dụ 6: Giải phương trình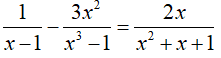

Lời giải

Chọn

Ví dụ 7: Tập nghiệm của phương trình (x² + 3x - 1)(3x² + 7x + 4) = 0 là:

Lời giải

Chọn C

Ví dụ 8: Phương trình (x² + 3x + 2)(3x² + 5x + 2) = 0 có:

Lời giải

Chọn C

Ví dụ 9: Tìm m để phương trình (x² + 2x + m)(x² + mx + 2) = 0 có ba nghiệm phân biệt.

Lời giải

Chọn D