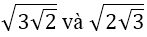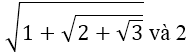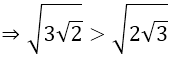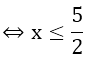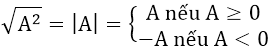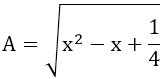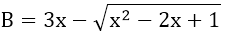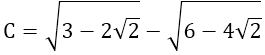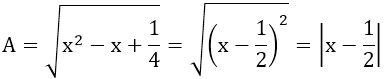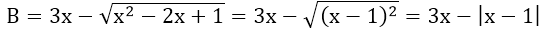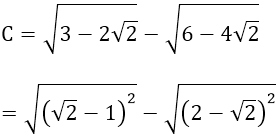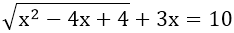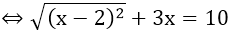Các dạng bài tập Toán 9 Chương 1 phần Đại số cực hay có đáp án | Toán lớp 9
Các dạng bài tập Toán 9 Chương 1 phần Đại số cực hay có đáp án
Với Các dạng bài tập Toán 9 Chương 1 phần Đại số cực hay có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 1 phần Đại số từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

I. Các dạng bài tập
- Các dạng toán về căn bậc hai lớp 9
- Liên hệ giữa căn bậc hai và hằng đẳng thức
- Liên hệ giữa phép nhân, phép chia và phép khai phương
- Bài Toán về biến đổi đơn giản biểu thức căn bậc 2
- Căn bậc ba
- Sử dụng biểu thức nhân liên hợp để giải toán chứa căn bậc hai, căn bậc ba
- Giải phương trình chứa dấu căn
- Lý thuyết Chương 1: Căn bậc hai, Căn bậc ba Xem chi tiết
- Chủ đề: Căn bậc hai Xem chi tiết
- Lý thuyết Căn bậc hai Xem chi tiết
- Dạng 1: So sánh căn bậc hai số học Xem chi tiết
- Dạng 2: Tìm điều kiện để √A có nghĩa Xem chi tiết
- Dạng 3: Rút gọn biểu thức chứa căn bậc hai (dạng √(A2)) Xem chi tiết
- Dạng 4: Tìm giá trị nhỏ nhất, giá trị lớn nhất của biểu thức chứa căn Xem chi tiết
- Bài tập tổng hợp về Căn bậc hai Xem chi tiết
- Chủ đề: Liên hệ phép nhân, phép chia với phép khai phương Xem chi tiết
- Bài tập Liên hệ phép nhân, phép chia với phép khai phương Xem chi tiết
- Chủ đề: Biến đổi đơn giản biểu thức chứa căn bậc hai Xem chi tiết
- Bài tập Biến đổi đơn giản biểu thức chứa căn bậc hai Xem chi tiết
- Chủ đề: Căn bậc ba Xem chi tiết
- Bài tập tổng hợp về Căn bậc ba Xem chi tiết
- Chủ đề: Dùng biểu thức liên hợp để giải toán Xem chi tiết
- Bài tập Dùng biểu thức liên hợp để giải toán Xem chi tiết
- Chủ đề: Giải phương trình chứa dấu căn Xem chi tiết
- Bài tập Giải phương trình chứa dấu căn Xem chi tiết
- Bài tập trắc nghiệm Toán 9 Căn bậc hai (có đáp án) Xem chi tiết
II. Lý thuyết & Trắc nghiệm theo bài học
- Lý thuyết Bài 1: Căn bậc hai (hay, chi tiết)
- Trắc nghiệm Bài 1: Căn bậc hai
- Lý thuyết Bài 2: Căn thức bậc hai và hằng đẳng thức (hay, chi tiết)
- Trắc nghiệm Bài 2: Căn thức bậc hai và hằng đẳng thức
- Lý thuyết Bài 3: Liên hệ giữa phép nhân và phép khai phương (hay, chi tiết)
- Trắc nghiệm Bài 3: Liên hệ giữa phép nhân và phép khai phương
- Lý thuyết Bài 4: Liên hệ giữa phép chia và phép khai phương (hay, chi tiết)
- Trắc nghiệm Bài 4: Liên hệ giữa phép chia và phép khai phương
- Lý thuyết Bài 5: Bảng căn bậc hai (hay, chi tiết)
- Trắc nghiệm Bài 5: Bảng căn bậc hai
- Lý thuyết Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai (hay, chi tiết)
- Trắc nghiệm Bài 6: Biến đổi đơn giản biểu thức chứa căn thức bậc hai
- Lý thuyết Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo) (hay, chi tiết)
- Trắc nghiệm Bài 7: Biến đổi đơn giản biểu thức chứa căn thức bậc hai (tiếp theo)
- Lý thuyết Bài 8: Rút gọn biểu thức chứa căn thức bậc hai (hay, chi tiết)
- Trắc nghiệm Bài 8: Rút gọn biểu thức chứa căn thức bậc hai
- Lý thuyết Bài 9: Căn bậc ba (hay, chi tiết)
- Trắc nghiệm Bài 9: Căn bậc ba
- Tổng hợp Lý thuyết Chương 1 Đại Số 9 (hay, chi tiết)
- Tổng hợp Trắc nghiệm Chương 1 Đại Số 9
Cách So sánh căn bậc hai số học
Phương pháp giải
Dựa vào tính chất: Nếu a, b ≥ 0 thì a < b ⇔ √a < √b
Ví dụ minh họa
Ví dụ 1:So sánh các số sau:
a) 9 và √80
b) √15 - 1 và √10
Hướng dẫn:
a) Ta có: 9 = √81. Vì √81 > √80 nên 9 > √80
b) Ta có: √15 - 1 < √16 - 1 = 3
√10 > √9 = 3
Vậy √15-1 < √10
Ví dụ 2:So sánh các số sau
a)
b) √10 + √5 + 1 và √35
c)
Hướng dẫn:
a) (3√2)2 = 32.(√2)2 = 9.2 = 18
(2√3)2 = 22.(√3)2 = 4.3 = 12
⇒ (3√2)2 > (2√3)2 ⇒ 3√2 > 2√3
b) Ta có: √10 + √5 + 1 > √9 + √4 + 1 = 6
mà √35 < √36 = 6
⇒ √10 + √5 + 1 > √35
c) Ta có: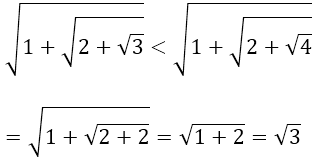
mà √3 < √4 = 2
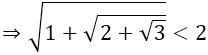
Tìm điều kiện để căn A có nghĩa
Phương pháp giải
√A có nghĩa ⇔ A ≥ 0
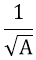
Ví dụ minh họa
Ví dụ 1: Tìm x để căn thức 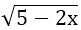
Hướng dẫn:
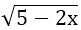
Ví dụ 2: Tìm x để căn thức 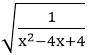
Hướng dẫn:
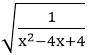
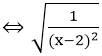
⇔ (x - 2)2 > 0 ⇔ x ≠ 2.
Cách Rút gọn biểu thức chứa căn bậc hai
Phương pháp giải
Vận dụng hằng đẳng thức:
Ví dụ minh họa
Ví dụ 1: Rút gọn các biểu thức sau:
a)
b)
c)
Hướng dẫn:
a)
Nếu x ≥ 1/2 thì A = x - 1/2
Nếu x < 1/2 thì A = 1/2 - x
b)
Nếu x ≥ 1 thì B = 3x - (x - 1) = 2x + 1
Nếu x < 1 thì B = 3x + (x - 1) = 4x - 1.
c)
= √2 - 1| - |2 - √2| = √2 - 1 - (2 - √2) = 2√2 - 3.
Ví dụ 2: Tìm x, biết:
Hướng dẫn:
⇔ |x - 2| + 3x = 10 (1)
Nếu x ≥ 2 thì |x - 2| = x - 2. Khi đó, phương trình (1) trở thành:
x - 2 + 3x = 10 ⇔ 4x = 12 ⇔ x = 3 (thuộc khoảng đang xét)
Nếu x < 2 thì |x - 2| = 2 - x. Khi đó, phương trình (1) trở thành:
2 - x + 3x = 10 ⇔ 2x = 8 ⇔ x = 4 (không thuộc khoảng đang xét)
Vậy giá trị x thỏa mãn là x = 3.