Lý thuyết Dấu hiệu nhận biết tiếp tuyến của đường tròn hay, chi tiết | Toán lớp 9
Lý thuyết Dấu hiệu nhận biết tiếp tuyến của đường tròn hay, chi tiết
Tài liệu Lý thuyết Dấu hiệu nhận biết tiếp tuyến của đường tròn hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Dấu hiệu nhận biết tiếp tuyến của đường tròn từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.
1. Tính chất của tiếp tuyến
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.
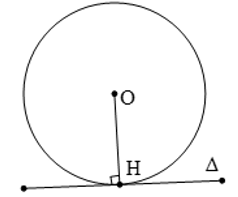
Trong hình vẽ Δ là tiếp tuyến ⇒ Δ ⊥ OH (H là tiếp điểm).
2. Dấu hiệu nhận biết tiếp tuyến của đường tròn.
Để nhận biết một đường thẳng là tiếp tuyến của một đường tròn ta có hai dấu hiệu sau:
+ Dấu hiệu 1: Đường thẳng và đường tròn chỉ có một điểm chung (định nghĩa tiếp tuyến).
+ Dấu hiệu 2: Đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó.
Cụ thể bằng các hiểu sau:
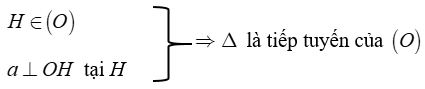
3. Ví dụ cụ thể
Câu 1: Cho tam giác ABC có AB = 3cm; Ac = 4cm; BC = 5cm. Vẽ đường tròn (B; BA). Chứng minh rằng AC là tiếp tuyến của đường tròn
Hướng dẫn:
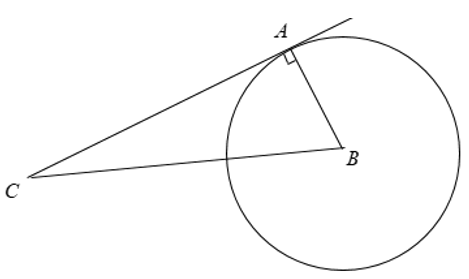
Ta có: AB2 + AC2 = BC2
⇒ ΔABC là tam giác vuông tại A.
hay AC ⊥ AB
Áp dụng dấu hiệu nhận biết của tiếp tuyến ta có:
+ AC với đường tròn (B) có một điểm chung là A.
+ Đường thẳng AC đi qua A và vuông góc với bán kính BA.
⇒ AC là tiếp tuyến của đường tròn (B; BA)
B. Bài tập tự luận
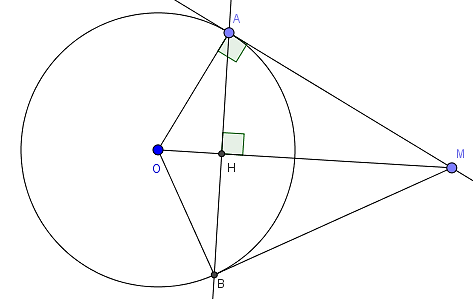
Câu 1: Cho đường tròn (O; 12), điểm M cách O 20. Vẽ tiếp tuyến AM với A là tiếp điểm
a) Tính MA
b) Vẽ dây AB vuông góc với OM. Chứng minh MB là tiếp tuyến
Lời giải:
a) Áp dụng định lý Py – ta – go ta có:
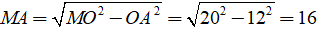
b) Gọi H là giao điểm của AB với OM
Xét hai tam giác OAH và OBH là hai tam giác vuông tại H
Có: OH chung; OA = OB = R
⇒ ΔOAH = ΔOBH nên HA = HB
Tam giác MAB có MH vừa là đường cao vừa là đường trung tuyến nên MAB cân tại M
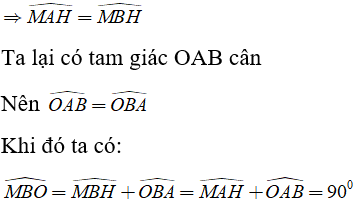
Vậy MB là tiếp tuyến của đường tròn
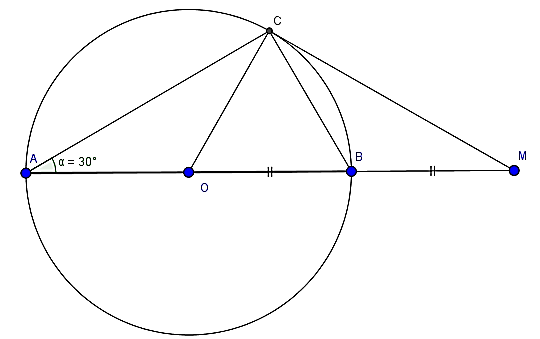
Câu 2: Cho đường tròn (O) đường kính AB. C là một điểm trên đường tròn sao cho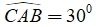 
. M là điểm đối xứng với O qua B. Chứng minh MC là tiếp tuyến của (O)
Lời giải:
