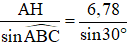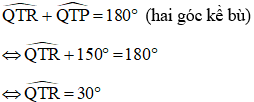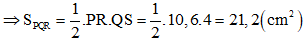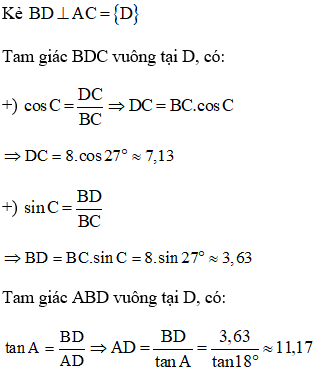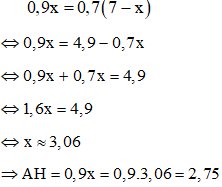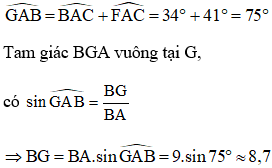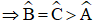Cách giải tam giác nhọn dựa vào các hệ thức trong tam giác vuông | Toán lớp 9
Cách giải tam giác nhọn dựa vào các hệ thức trong tam giác vuông
Với Cách giải tam giác nhọn dựa vào các hệ thức trong tam giác vuông Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải tam giác nhọn dựa vào các hệ thức trong tam giác vuông từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
A. Phương pháp giải
Nhắc lại kiến thức
Trong một tam giác vuông, nếu cho trước hai cạnh hoặc một cạnh và một góc nhọn thì ta sẽ tìm được tất cả các cạnh và các góc còn lại của nó.
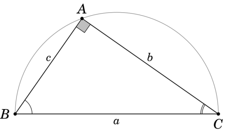
Cho tam giác ABC vuông tại A, cạnh huyền a và các cạnh góc vuông b, c.
1. Định lý: Trong một tam giác vuông, mỗi cạnh góc vuông bằng
- Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề.
- Cạnh góc vuông kia nhân với tan góc đối hoặc nhân với cot góc kề.
2. Như vậy, trong tam giác ABC vuông tại A, ta có hệ thức
• b = a.sinB = a.cosC = c.tanB = c.cotC
• c = a.sinC = a.cosB = b.tanC = b.cotB
A. Phương pháp giải
• Kẻ thêm đường cao xuống cạnh kề của góc đã biết.
• Chuyển bài toán về giải tam giác vuông biết một cạnh và một góc.
B. Ví dụ minh họa
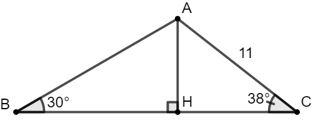
Ví dụ 1: Trong tam giác ABC có AC = 11 cm,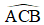 
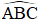
= 28o, 
= 30o, H là chân đường vuông góc kể từ A đến BC. Tính AB.
Hướng dẫn giải:
Do AH ⊥ BC ⇒ ΔAHB và ΔAHC là hai tam giác vuông.
Xét tam giác AHC vuông tại H có: AH = AC.sin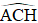
= 11.sin38o ≈ 6,78 (cm)
Xét tam giác AHB vuông tại H có:
Vậy AB = 13,56 cm.
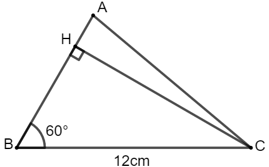
Ví dụ 2: Cho tam giác ABC có BC = 12 cm,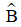 
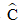
= 60o, 
= 40o. Tính
a) Đường cao CH và cạnh AC
b) Diện tích tam giác ABC
Hướng dẫn giải:
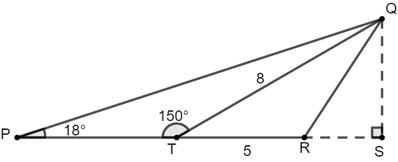
Ví dụ 3: Cho hình dưới đây. Biết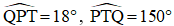 
, QT = 8 cm, TR = 5 cm.
Hãy tính:
a) PT
b) Diện tích tam giác PQR
Hướng dẫn giải:
Từ Q dựng QS ⊥ PR, S ∈ PR
a) Ta có:
+) Xét tam giác QST vuông tại S có: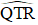 
= 30o
⇒ QS =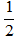 
QT (cạnh góc vuông đối diện góc 30o)
Vậy QS = 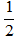.8 = 4cm
+) Áp dụng định lý Py – ta – go cho tam giác vuông QST có:
TS2 = QT2 - QS2 = 82 - 42 = 48 ⇒ TS =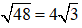 
cm
+) Xét tam giác vuông QSP có:
PS =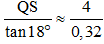 
= 12,5 cm
⇒ PT = PS - TS = 12,5 -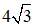 
≈ 5,6 cm
b) Ta có: PR = PT + TR = 5,6 + 5 = 10,6 cm
+) Xét tam giác PQR có đường cao QS
C. Bài tập trắc nghiệm
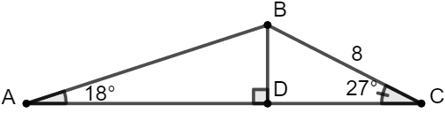
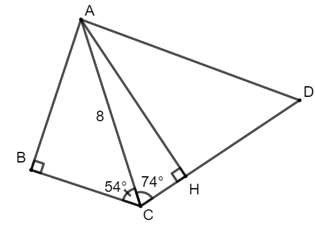
Bài 1: Cho tam giác ABC có góc A bằng 18o, góc C bằng 27o, cạnh BC = 8. Khi đó độ dài cạnh AC là (làm tròn đến chữ số thập phân thứ hai).
Hướng dẫn giải:
Suy ra AC = AD + DC ≈ 11,17 + 7,13 = 18,3
Bài 2: Cho tam giác ABC có BC = 7,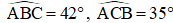 
. Gọi H là chân đường cao của tam giác ABC kẻ từ A. Hãy tính AH (làm tròn kết quả đến chữ số thập phân thứ hai).
A. 2,75
B. 3,75
C. 3,4
D. 2,4
Hướng dẫn giải:
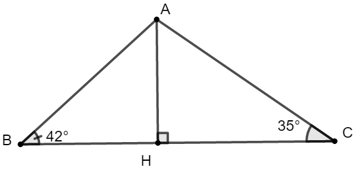
Gọi độ dài đoạn BH là x ( 0 < x < 7, cm) ⇒ CH = BC – BH = 7 – x (cm)
Xét tam giác ABH vuông tại H có: AH = BH.tan42o ≈ 0,9x
Xét tam giác ACH vuông tại H có: AH = CH.tan35o ≈ 0,7 (7 - x)
Vậy suy ra:
Đáp án A.
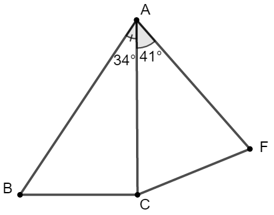
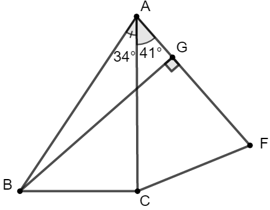
Bài 3: Cho hình vẽ sau, biết AB = 9,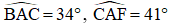 
. Khi đó khoảng cách từ điểm B đến cạnh AF bằng (làm tròn kết quả đến chữ số thập phân thứ nhất)
A. 8,7
B. 5,3
C. 3,8
D. 4,7
Hướng dẫn giải:
Kẻ BG ⊥ AF = {G}
Khi đó khoảng cách từ điểm B đến cạnh AF bằng BG.
Vậy khoảng cách từ điểm B đến cạnh AF bằng 8,7.
Đáp án A.
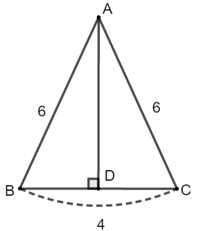
Bài 4: Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Góc nhỏ nhất của tam giác đó bằng (làm tròn đến phút)
A. ≈ 30o56'
B. ≈ 38o56'
C. ≈ 40o53'
D. ≈ 15o36'
Hướng dẫn giải:
+) Xét ΔABC có: AB = AC > BC (8 = 6 > 4) 
Vậy góc nhỏ nhất của tam giác đó là góc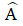 
.
+) Kẻ AD ⊥ BC = {D}
Xét ΔABC có AB = AC = 6 cm nên ΔABC là tam giác cân tại A.
Ta có: AD là đường cao trong tam giác cân
Suy ra AD đồng thời là tia phân giác của góc A và là đường trung tuyến trong tam giác ABC
Đáp án B.
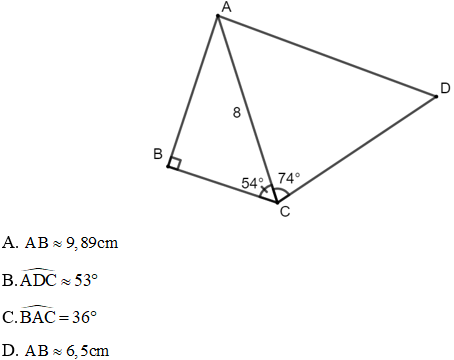
Bài 5: Cho hình vẽ dưới đây với AC = 8cm, AD = 9,6cm,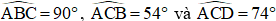 
. Khẳng đinh nào dưới đây là sai?
Hướng dẫn giải:
Đáp án A.
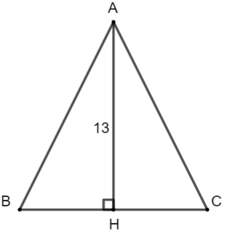
Bài 6: Cho tam giác ABC cân tại A, đường cao AH. Biết 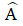= 48o; AH = 13cm. Chu vi của tam giác ABC là bao nhiêu? (làm tròn kết quả đến hàng đơn vị)
Hướng dẫn giải:
Tam giác ABC cân tại A có AH là đường cao nên AH đồng thời là đường trung tuyến và đường phân giác tại đỉnh A
Vậy chu vi của tam giác ABC bằng AB + AC + BC = 14,2 + 14,2 + 11,6 = 40 (cm)
