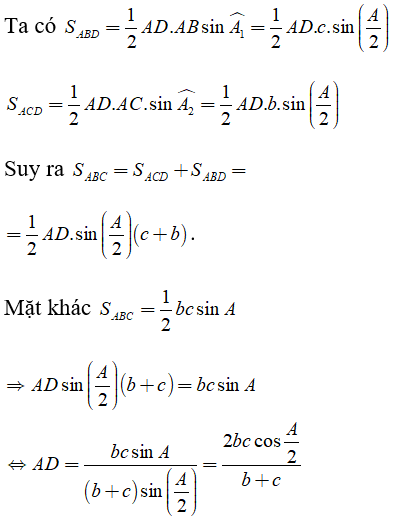Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông hay, chi tiết | Toán lớp 9

Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông hay, chi tiết

Tài liệu Lý thuyết Một số hệ thức về cạnh và góc trong tam giác vuông hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Một số hệ thức về cạnh và góc trong tam giác vuông từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Các hệ thức trong tam giác vuông.

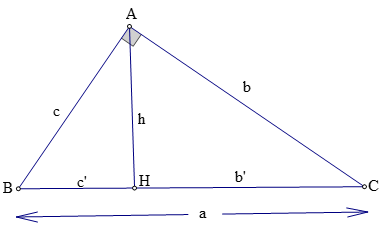
Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

    + Cạnh huyền nhân với sin góc đối hay nhân với côsin góc kề.

    + Cạnh góc vuông kia nhân với tan của góc đối hay nhân với cotg của góc kề.

    b = a.sinB = a.cosC; c = a.sinC = a.cosB; b = c.tgB = c.cotgC; c = b.tgC = b.cotgC.

Chú ý: Trong một tam giác vuông nếu cho trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông) thì ta sẽ tìm được các yếu tố còn lại.

2. Ví dụ cụ thể

Câu 1: Cho tam giác ABC có AB = 16, AC = 14 và ∠B = 60°.

a) Tính độ dài cạnh BC.

b) Tính diện tích tam giác ABC.

Hướng dẫn:

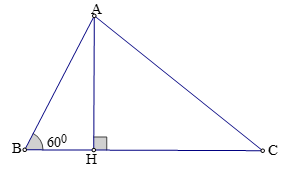
a) Kẻ đường cao AH.

Xét tam giác vuông ABH, ta có: BH = AB.cosB = AB.cos60° = 16.(1/2) = 8.

AH = AB.sinB = AB.sin60° = 16.(√3)/2 = 8√3

Áp dụng định lý Py – ta – go vào tam giác vuông AHC ta có:

HC² = AC² - AH² = 14² - (8√3)² = 196 - 192 = 4. Suy ra HC = 2.

Vậy BC = CH + HB = 2 + 8 = 10

b) Ta có:

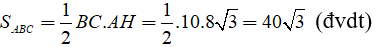
Câu 2: Một con thuyền băng qua một khúc sông với vận tốc là 3 km/h trong vòng 6 phút. Biết rằng hướng thuyền đi tạo với bờ một góc 60 độ. Tính chiều dài (m) của khúc sông đó.

Giải:

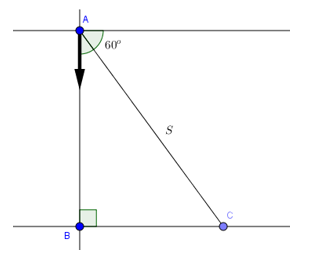
Ta giải bài toán thông qua hình vẽ trên

Nhận thấy ∠BAC = 30^o

Ta đổi: 3(km/h) = 5/6(m/s); 6 phút = 360 giây

Khi đó ta có: S = (5/6). 360 = 300(m)

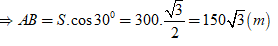
B. Bài tập tự luận

Câu 1: Tính diện tích tam giác ABC biết 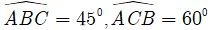bán kính đường tròn ngoại tiếp tam giác ABC là R.

Lời giải:

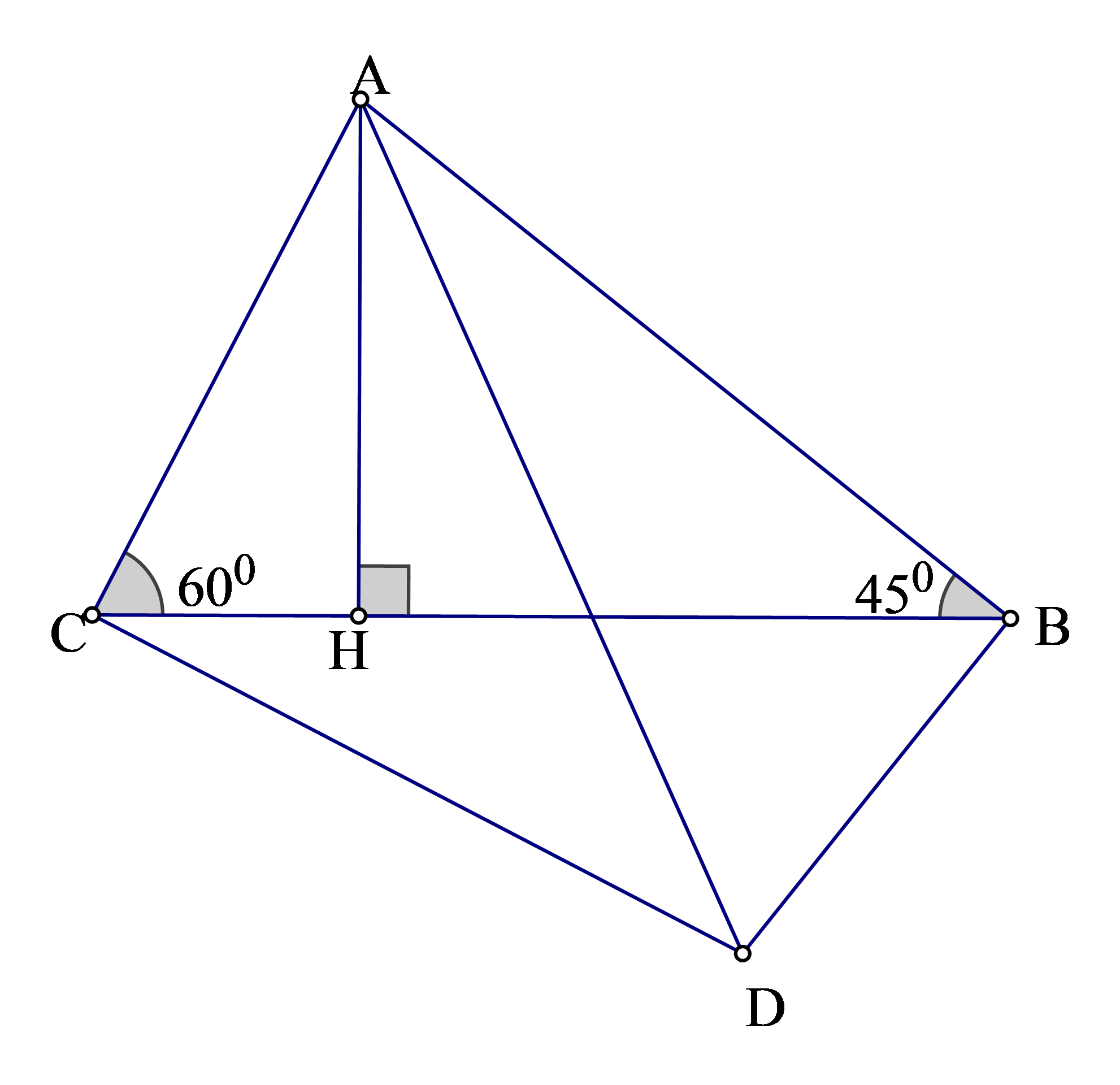
Giả thiết có các góc có số đo đặc biệt, nhưng tam giác ABC là tam giác thường nên ta sẽ tạo ra tam giác vuông bằng cách dựng các đường thẳng qua C, B lần lượt vuông góc với AC, AD.

Gọi D là giao điểm của hai đường thẳng trên.

Khi đó tam giác ABD và ACD là các tam giác vuông và 4 điểm A, B, C, D cùng nằm trên đường tròn đường kính AD = 2R.

Ta có: Ta có: .

Câu 2: Cho tam giác ABC với các đỉnh A, B, C và các cạnh đối diện với các đỉnh tương ứng là: a, b, c. Chứng minh rằng:

a) a² = b² + c² - 2bccosA

b) Gọi D là chân đường phân giác trong góc A . Chứng minh:

Lời giải:

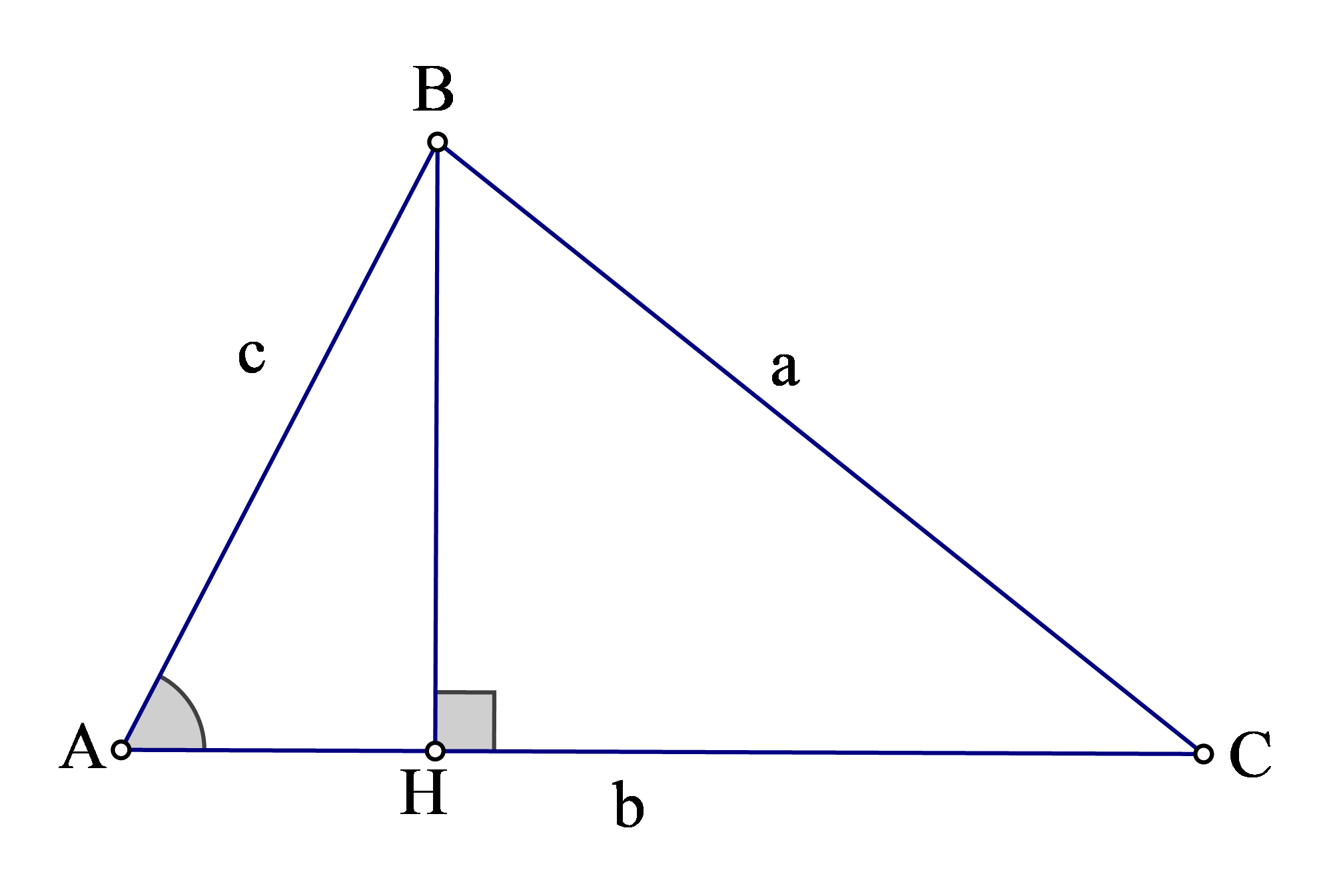
a) Dựng đường cao BH của tam giác ABC ta có:

Giả sử H thuộc cạnh AC .

Ta có: AC = AH + HC.

Áp dụng định lý Pi ta go cho các tam giác vuông AHB, BHC ta có:

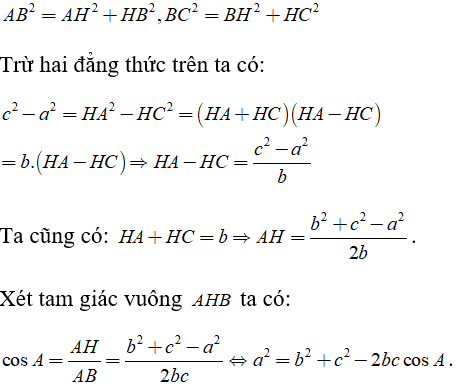
b) Để chứng minh bài toán ta cần kết quả sau:

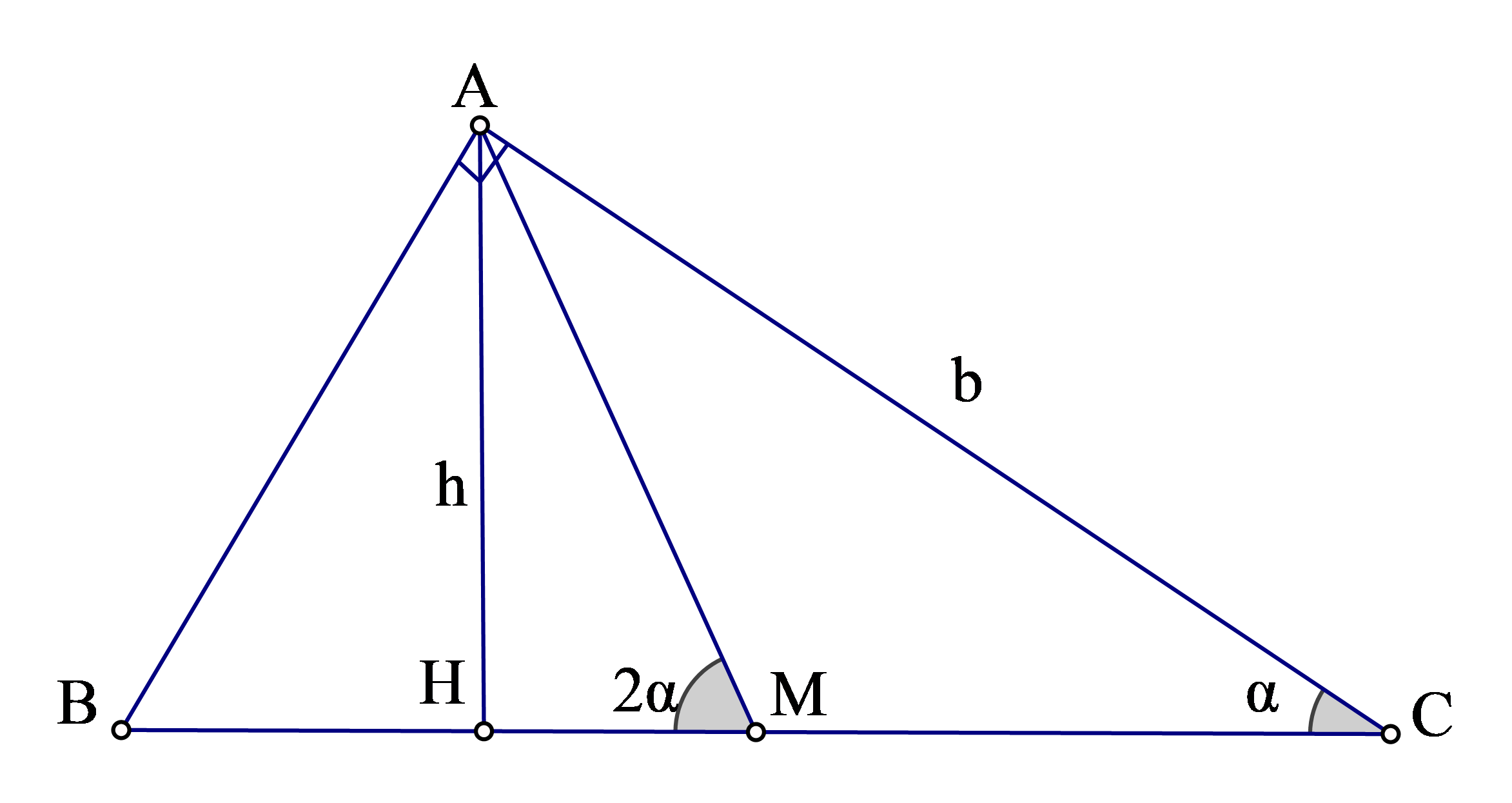
Xét tam giác ABC . Dựng đường cao BE ta có:

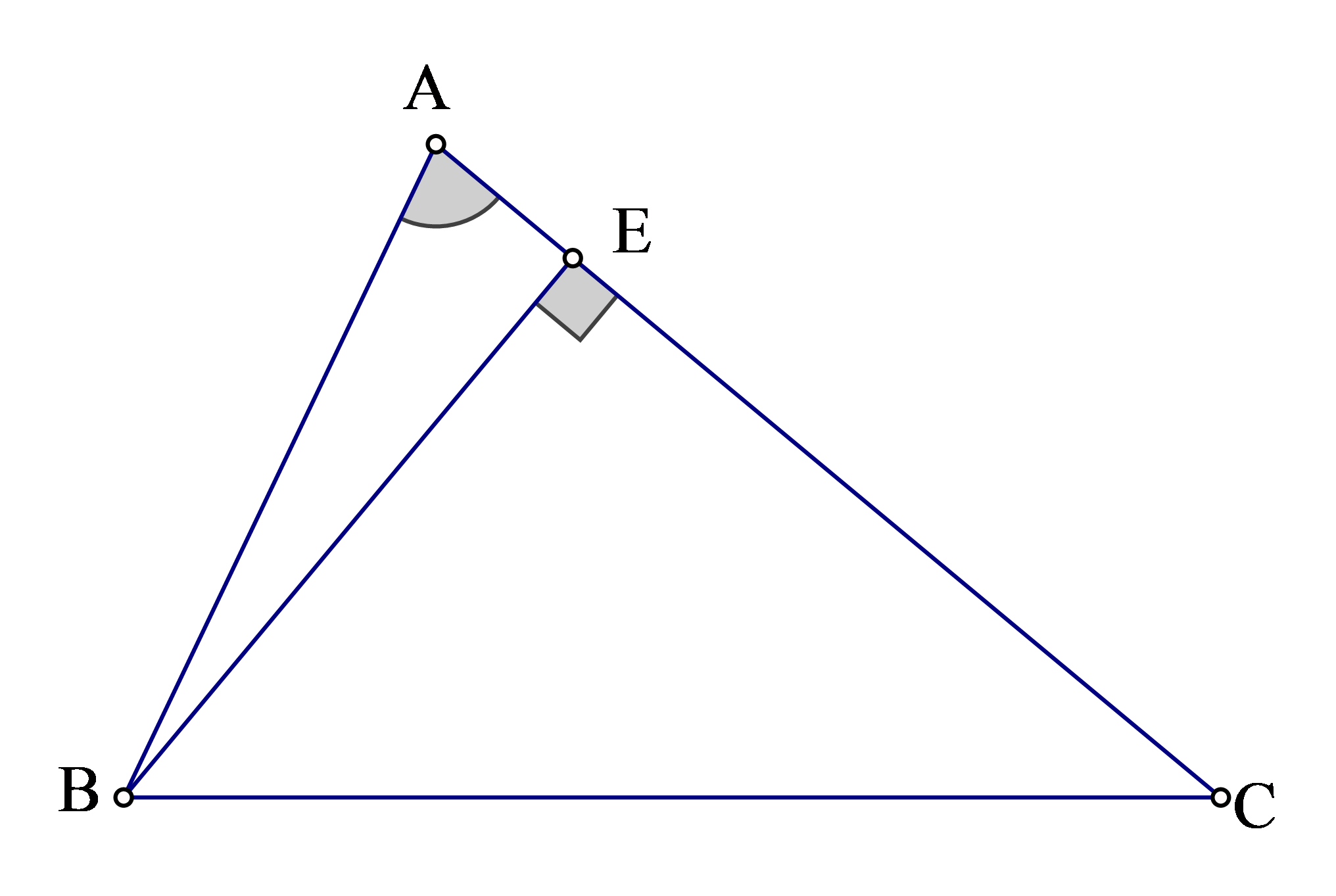
Trở lại bài toán: