Sử dụng biểu thức nhân liên hợp để giải toán chứa căn bậc hai, căn bậc ba | Toán lớp 9

Sử dụng biểu thức nhân liên hợp để giải toán chứa căn bậc hai, căn bậc ba

Với Sử dụng biểu thức nhân liên hợp để giải toán chứa căn bậc hai, căn bậc ba Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Sử dụng biểu thức nhân liên hợp để giải toán chứa căn bậc hai, căn bậc ba từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

I. Lý thuyết

Một số biểu thức liên hợp thường gặp:

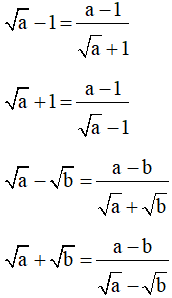
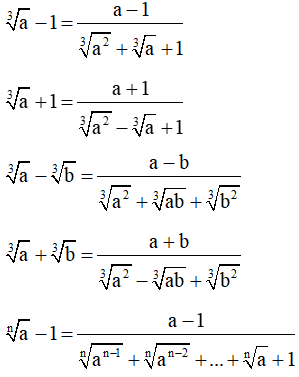
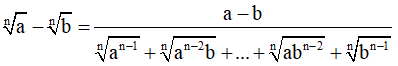
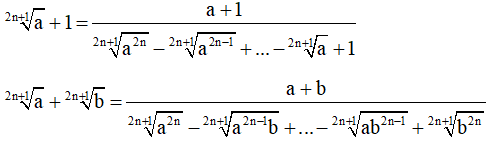
II. Dạng bài tập

Dạng 1: Sử dụng căn bậc 2, căn bậc 3 để tính giá trị biểu thức.

Phương pháp giải: Sử dụng các phép nhân liên hợp để biến đổi biểu thức ban đầu thành những biểu thức đơn giản hơn sau đó thực hiện theo thứ tự phép tính.

Ví dụ: Tính

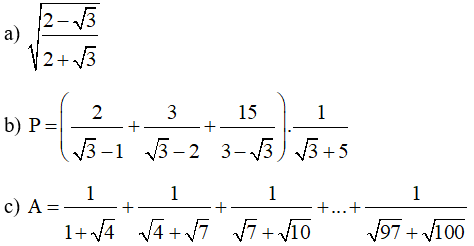
Lời giải:

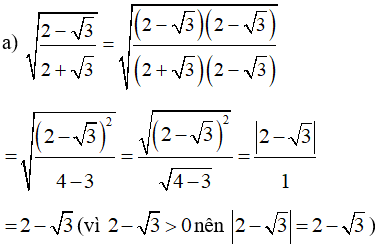
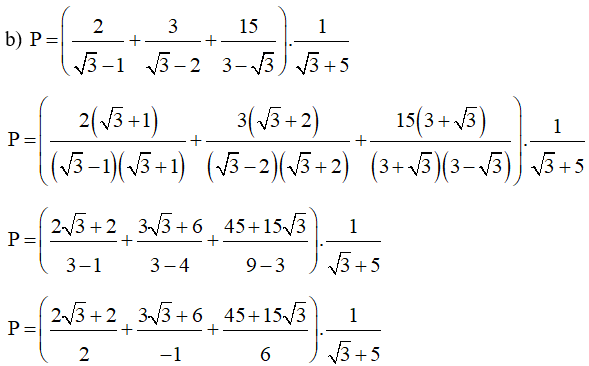
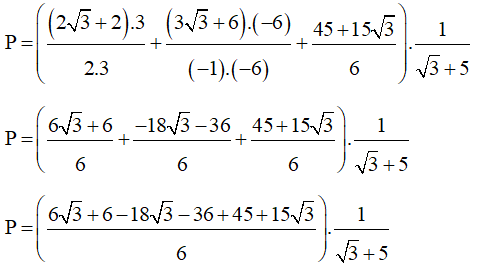
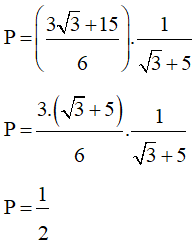
c)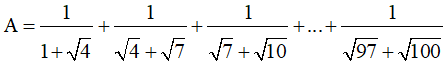

Xét biểu thức:

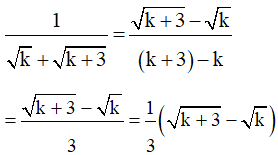
Cho k các giá trị từ 1; 4; 7;…;97 ta được:

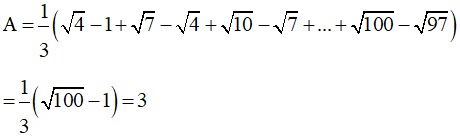
Dạng 2: Sử dụng biểu thức nhân liên hợp để rút gọn biểu thức có chứa căn bậc 2, căn bậc 3.

Phương pháp giải: Dùng biểu thức liên hợp để biến đổi và rút gọn biểu thức.

Ví dụ: Rút gọn biểu thức sau:

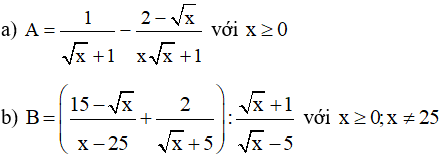
Lời giải:

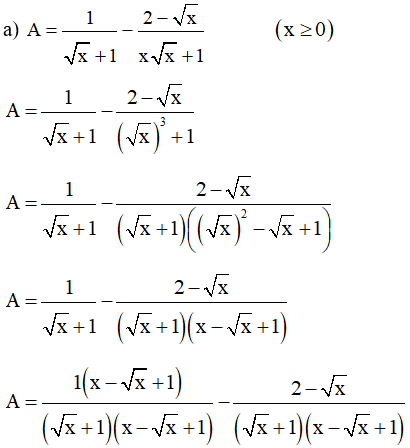
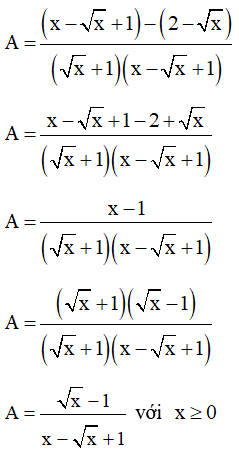
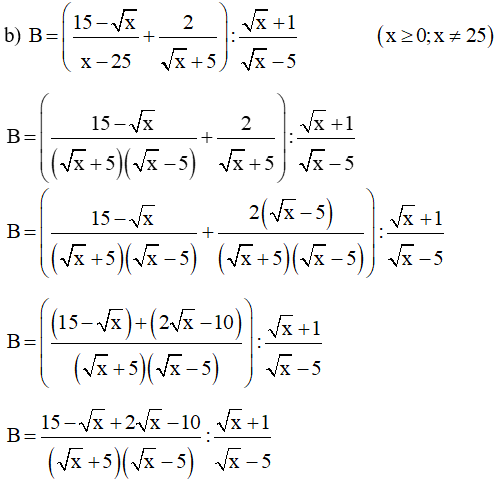
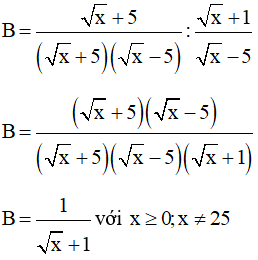
Dạng 3: Chứng minh x₀ là nghiệm của phương trình

Phương pháp giải: Dùng các biểu thức liên hợp để đưa nghiệm x₀ về số đơn giản có thể tính toán được. Sau đó thay x₀ vào phương trình và chứng minh x₀ là nghiệm.

Ví dụ: Chứng minh 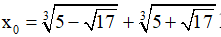là nghiệm của phương trình x³ - 6x - 10 = 0

Lời giải:

Ta có:

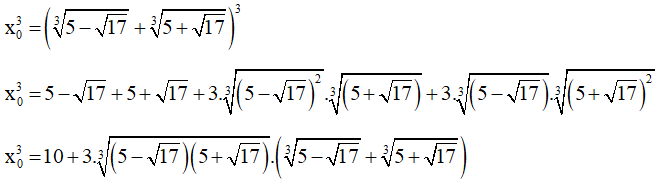
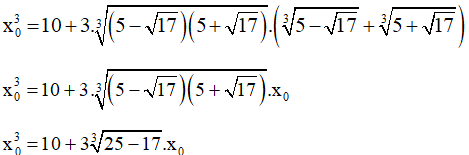
x₀³ = 10 + 3³√8.x₀

x₀³ = 10 + 3.2.x₀

x₀³ = 10 + 6x₀

x₀³ - 6x₀ - 10 = 0

Vậy x₀ là nghiệm của phương trình x³ - 6x - 10 = 0.

III. Bài tập tự luyện.

Bài 1: Thực hiện phép tính

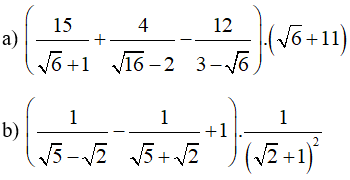
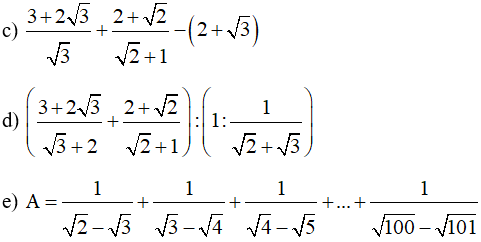
Bài 2: Rút gọn biểu thức

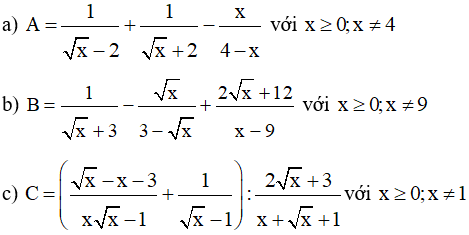
Bài 3: Chứng minh 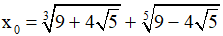là nghiệm của phương trình x³ - 3x - 18 = 0

Bài 4: Cho 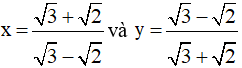. Tính giá trị biểu thức: A = 5x² + 6xy + 5y²