Lý thuyết, cách giải bài tập về Đường tròn hay, chi tiết | Toán lớp 9

Lý thuyết, cách giải bài tập về Đường tròn hay, chi tiết

Với Lý thuyết, cách giải bài tập về Đường tròn hay, chi tiết Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

I. Lý thuyết chung về Đường tròn

1. Đường tròn tâm O, bán kính R, kí hiệu (O, R) là hình gồm các điểm cách điểm O cho trước một khoảng bằng R

2. Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn

3. Đường tròn là hình có tâm đối xứng và trục đối xứng

- Tâm đối xứng là tâm của đường tròn

- Trục đối xứng là bất kì đường kính nào

4. Trong các dây của đường tròn, đường kính là dây lớn nhất.

5. Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. Đảo lại, trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

6. Trong một đường tròn:

- Hai dây bằng nhau thì cách đều tâm

- Hai dây cách đều tâm thì bằng nhau

7. Trong hai dây của một đường tròn:

- Dây nào lớn hơn thì gần tâm hơn

- Dây nào gần tâm hơn thì dây đó lớn hơn.

II. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC cân tại A. Gọi E là trung điểm của BC và BD là đường cao của ΔABC (D ∈ AC). Gọi giao điểm của AE và BD là H.

a) Chứng minh rằng bốn điểm A, D, E, B cùng thuộc một đường tròn tâm O

b) Xác định tâm I của đường tròn đi qua 3 điểm H; D; C

c) Chứng minh rằng đường tròn tâm O và đường tròn tâm I có hai điểm chung

Hướng dẫn:

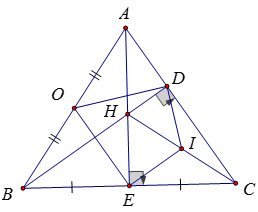
a) Do tam giác ABC cân tại A nên AE ⊥ BC

Gọi O là trung điểm của đoạn thẳng AB. Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông ta có:

Trong ΔDAB vuông tại D có DO là trung tuyến

⇒ OA = OB = OD

Trong ΔDAB vuông tại D có DO là trung tuyến

⇒ OA = OB = OD

Trong ΔABE vuông tại E có EO là trung tuyến

⇒ OA = OB = OE

⇒ OA = OB = OE = OD

⇒ Vậy A, B, E, D cũng thuộc đường tròn (O)

b) Gọi I là trung điểm của HC

Trong ΔHDC vuông tại D có DI là trung tuyến

⇒ ID = IH = IC

⇒ I là tâm đường tròn đi qua 3 điểm H, D, C

c) Trong ΔHEC vuông tại E có EI là trung tuyến

⇒ IE = IH = IC

⇒ E thuộc đường tròn (I)

Vậy (O) và (I) có hai điểm chung là E và D.

Ví dụ 2: Cho tam giác ABC, cạnh BC cố định, đường trung tuyến BM = 1,5 cm. Hỏi:

a) Trọng tâm G của tam giác di động trên đường nào?

b) Đỉnh A di động trên đường nào?

Hướng dẫn:

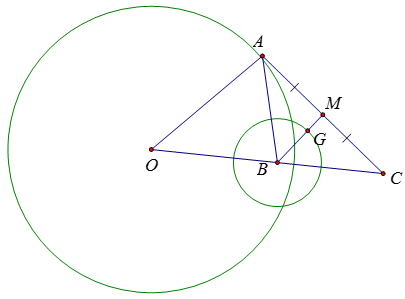
a) Vì G là trọng tâm của tam giác ABC nên

BG = 2/3; BM = 2/3.1,5 = 1 (cm)

Điểm G cách điểm B cho trước một khoảng là 1 cm nên G nằm trên đường tròn

(B; 1cm)

b) Trên tia đối của tia BC lấy điểm O sao cho BC = OB. Do BC cố định là O là cố định.

Ta có BM là đường trung bình của tam giác OAC nên OA = 2; BM = 3 cm

Do đó, điểm A nằm trên đường tròn (O; 3cm)

Nhận xét: Sẽ rất sai lầm nếu nói A nằm trên đường tròn tâm B, bán kính BA. Sai lầm ở chỗ đọ dài BA luôn thay đổi.

Ví dụ 3: Cho điểm M nằm trong đường tròn tâm O, M không trùng với O. Chứng minh rằng trong tất cả các dây đi qua M thì dây vuông góc với OM là dây ngắn nhất.

Hướng dẫn:

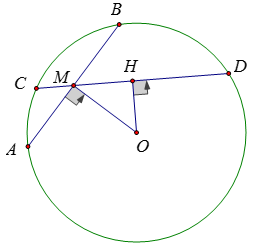
Gọi dây AB là dây đi qua M và OM vuông góc với AB; dây CD là dây đi qua M nhưng không vuông góc với OM. Ta phải chứng minh AB < CD

Vẽ OH ⊥ CD. Ta có: OH < OM (quan hệ giữa đường vuông góc và đường xiên)

⇒ CD > AB ( dây nào gần tâm hơn thì lớn hơn)

Vậy AB < CD