Lý thuyết Hệ thức Vi-ét và ứng dụng hay, chi tiết | Toán lớp 9

Lý thuyết Hệ thức Vi-ét và ứng dụng hay, chi tiết

Tài liệu Lý thuyết Hệ thức Vi-ét và ứng dụng hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Hệ thức Vi-ét và ứng dụng từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

1. Hệ thức vi – ét

Phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có nghiệm dù đó là hai nghiệm phân biệt hay nghiệm kép thì ta đều có thể viết được dưới dạng:

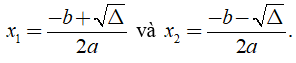
Khi đó nếu x₁, x₂ là hai nghiệm của phương trình ax² + bx + c = 0 (a ≠ 0) thì ta có:

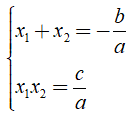
2. Ứng dụng của định lý Vi – ét

a) Tính nhẩm nghiệm

    + Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có một nghiệm là x₁ = 1 và nghiệm còn lại là x₂ = c/a

    + Nếu phương trình ax² + bx + c = 0 (a ≠ 0) có a - b + c = 0 thì phương trình có một nghiệm là x₁ = -1 và nghiệm còn lại là x₂ = -c/a

b) Tìm hai số khi biết tổng và tích.

    + Nếu hai số có tổng bằng S và tích bằng P thì hai số đó là nghiệm của phương trình bậc hai x² - Sx + P = 0

    + Điều kiện để có hai số đó là S² - 4P ≥ 0

3. Ví dụ cụ thể

Câu 1: Cho phương trình x² - 3x + 2 = 0. Tính giá trị của biểu thức P = 2(x₁ + x₂) - x₁.x₂

Hướng dẫn:

Ta có: Δ = (-3)² - 4.1.2 = 1 ⇒ phương trình có hai nghiệm phân biệt x₁, x₂.

Áp dụng hệ thức Vi – ét ta có:

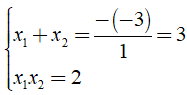
Khi đó P = 2(x₁ + x₂) - x₁.x₂ = 2.3 - 2 = 4. Vậy P = 4

Câu 2: Tìm hai số khi biết tổng hai số đó là S = 5 và tích của hai số đó là P = 6 ?

Hướng dẫn:

Gọi x₁, x₂ là hai số cần tìm, khi đó x₁, x₂ là nghiệm của phương trình x² - 5x + 6 = 0

Ta có Δ = (-5)² - 4.1.6 = 25 - 24 = 1 > 0

Khi đó phương trình có hai nghiệm là:

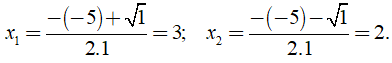
Vậy hai số cần tìm là 3 và 2.

B. Bài tập tự luận

Câu 1: Tìm hai số biết tổng của chúng bằng 5 và tích của chúng bằng 6.

Lời giải:

Gọi hai số đó là x₁ và x₂

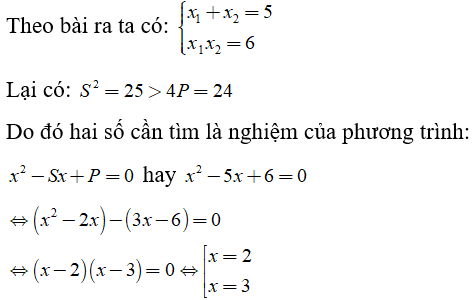
Vậy hai số cần tìm là 2 và 3.

Câu 2: Tìm hai số biết hiệu của chúng bằng 11 và tích của chúng bằng 60.

Lời giải:

Gọi hai số cần tìm là a, b