Bài tập Vị trí tương đối của đường thẳng và đường tròn chọn lọc, có đáp án | Toán lớp 9

Bài tập Vị trí tương đối của đường thẳng và đường tròn chọn lọc, có đáp án

Với Bài tập Vị trí tương đối của đường thẳng và đường tròn chọn lọc, có đáp án Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Vị trí tương đối của đường thẳng và đường tròn từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Đường thẳng và đường tròn có nhiều nhất bao nhiêu điểm chung

A. 1

B. 2

C.3

D. 4

Lời giải:

Đường thẳng và đường tròn có nhiều nhất hai điểm chung

Chọn đáp án B

Câu 2: Nếu đường thẳng và đường tròn có duy nhất một điểm chung thì

A. đường thẳng tiếp xúc với đường tròn

B. đường thẳng cắt đường tròn

C. đường thẳng không cắt đường tròn

D. đáp án khác

Lời giải:

Đường thẳng và đường tròn chỉ có một điểm chung thì đường thẳng tiếp xúc với đường tròn

Chọn đáp án A

Câu 3: Nếu đường thẳng d là tiếp tuyến của đường tròn (O) tại A thì

A. d // OA

B. d ≡ OA

C. d ⊥ OA tại A

D. d ⊥ OA tại O

Lời giải:

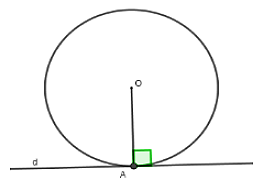
Nếu một đường thẳng là tiếp tuyến của một đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm

Nên d ⊥ OA tại tiếp điểm A

Chọn đáp án C

Câu 4: Cho đường tròn (O) và đường thẳng a. Kẻ OH ⊥ a tại H, biết OH > R khi đó đường thẳng a và đường tròn (O)

A. cắt nhau

B. không cắt nhau

C. tiếp xúc

D. đáp án khác

Lời giải:

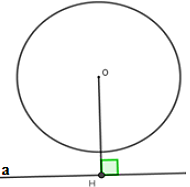
Vì OH > R nên α không cắt (O)

Chọn đáp án B

Câu 5: Điền vào các vị trí (1); (2) trong bảng sau (R là bán kính của đường tròn, d là khoảng cách từ tâm đến đường thẳng):

A. (1): cắt nhau; (2): 8cm

B. (1): 9cm ; (2): cắt nhau

C. (1): không cắt nhau; (2): 8cm

D. (1): cắt nhau; (2): 6cm

Lời giải:

+ Vì d < R (4cm < 5cm) nên đường thẳng cắt đường tròn

+ Vì đường thẳng tiếp xúc với đường tròn nên d = R = 8cm

Chọn đáp án A

Câu 6: Trên mặt phẳng tọa độ Oxy, cho điểm A( 5; 6). Xác định vị trí tương đối của đường tròn (A; 5) với các trục tọa độ?

A. Đường tròn tiếp xúc trục Oy.

B. Đường tròn tiếp xúc với trục Ox.

C. Đường tròn không cắt trục Ox.

D. Đường tròn không cắt trục Oy.

Lời giải:

Ta có khoảng cách từ A đến trục Ox bằng 6 > R.

Đường tròn (A; R) cắt trục Ox tại 2 điểm phân biệt .

Khoảng cách từ A đến trục Oy bằng 5 = R..

Do đó, đường tròn (A; R) tiếp xúc với trục Oy.

Chọn đáp án A

Câu 7: Cho đường tròn tâm (O; 3) và điểm A cách O một khoảng 5 cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính AB

A. AB = 3cm

B. AB = 5cm

C. AB = 4cm

D. Đáp án khác

Lời giải:

Do AB là tiếp tuyến của đường tròn (O) với B là tiếp điểm nên ta có:

OA² = OB² + AB²

⇒ AB² = OA² - OB² = 5² - 3² = 16

⇒ AB = 4cm

Chọn đáp án C.

Câu 8: Cho đường tròn (O; 6cm). Điểm M cách điểm O một khoảng 4cm. Hỏi qua M kẻ được bao nhiêu tiếp tuyến đến đường tròn?

A. 1

B.2

C. Vô số

D. 0

Lời giải:

Ta có: OM = 4 cm và R = 6 cm nên OM < R

Do đó, điểm M nằm trong đường tròn (O).

Suy ra, qua điểm M không kẻ được tiếp tuyến nào đến đường tròn

Chọn đáp án D.

Câu 9: Cho đường tròn , cho điểm A thỏa mãn: IA = 2√2. Hỏi qua điểm A kẻ được bao nhiêu tiếp tuyến đến đường tròn?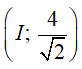

A. 1

B. 0

C. 2

D. Vô số

Lời giải:

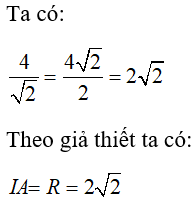
Do đó, điểm A nằm trên đường tròn đã cho. Khi đó, qua điểm A ta vẽ được đúng 1 tiếp tuyến đến đường tròn (I).

Chọn đáp án A.

Câu 10: Cho tam giác ABC vuông tại A có AB = 6 cm và BC = 10 cm . Vẽ đường tròn ( A; 6). Hỏi qua C dựng được bao nhiêu tiếp tuyến đến đường tròn?

A. 0

B. 1

C.2

D. Vô số

Lời giải:

Áp dụng định lí Pytago vào tam giác ABC ta có:

BC² = AB² + AC²

⇒ AC²= BC² - AB² = 10² - 6² = 64

⇒ AC = 8cm

Ta có: AC > R (8 > 6) nên điểm C nằm ngoài đường tròn (A ; 6).

Do đó, qua điểm C ta vẽ được hai tiếp tuyến đến đường tròn.

Chọn đáp án C.