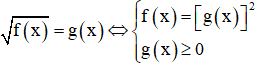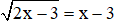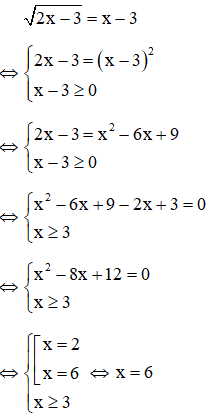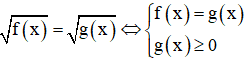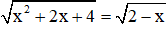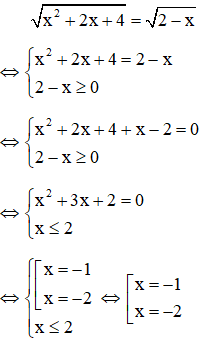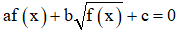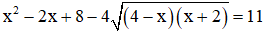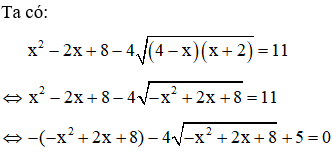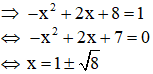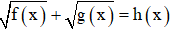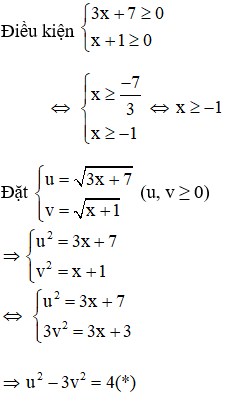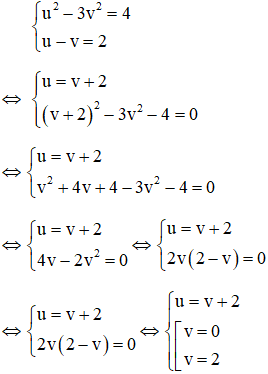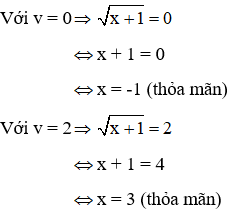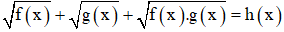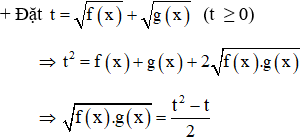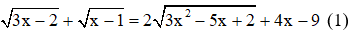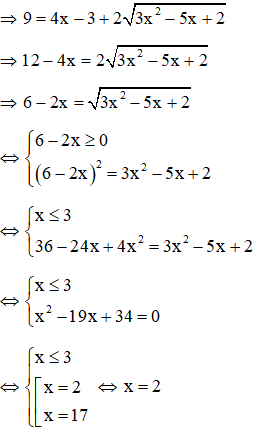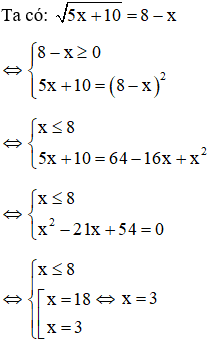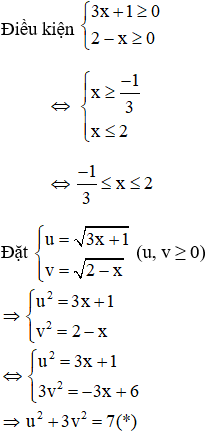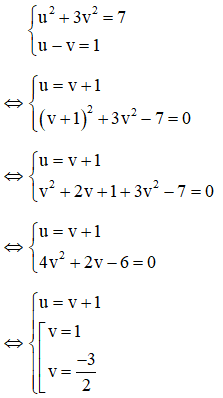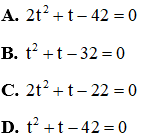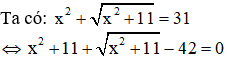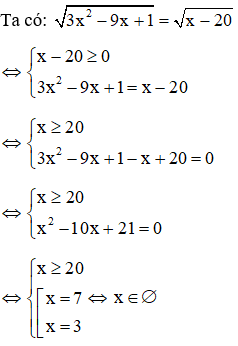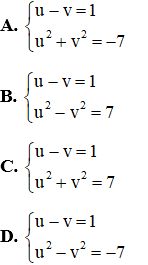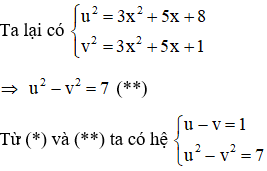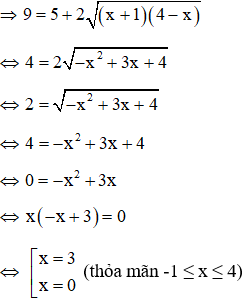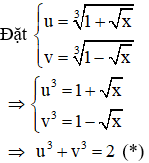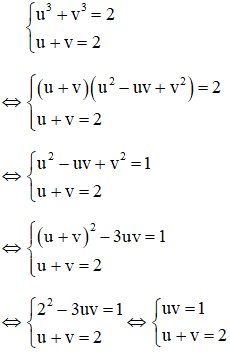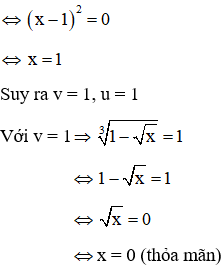Cách giải phương trình chứa căn thức lớp 9 cực hay | Toán lớp 9

Cách giải phương trình chứa căn thức lớp 9 cực hay

Với Cách giải phương trình chứa căn thức lớp 9 cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình chứa căn thức từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải

Để giải phương trình chứa ẩn dưới dấu căn ta tìm cách khử dấu căn. Hai cách hay dùng là:

- Nâng hai vế của phương trình lên một lũy thừa

- Đặt ẩn phụ

Dạng 1:

Ví dụ: Giải phương trình

Giải

Vậy phương trình có một nghiệm x = 6

Dạng 2:

Chú ý: Điều kiện g(x) ≥ 0 có thể thay bởi f(x) ≥ 0

Ví dụ: Giải phương trình

Giải

Vậy phương trình có hai nghiệm x = -1, x = -2

Dạng 3:

Đặt 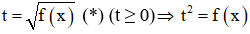. Khi đó phương trình đã cho trở thành: at² + bt + c = 0

Giải phương trình trên tìm t thỏa mãn điều kiện t ≥ 0 rồi sau đó thay vào biểu thức (*) tìm x

Ví dụ: Giải phương trình

Giải

Đặt 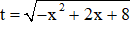(*) (t ≥ 0) ⇒ t² = -x² + 2x + 8. Khi đó phương trình đã cho trở thành: -t² - 4t + 5 = 0

Phương trình có a + b + c = -1 + (-4) +5 = 0 nên có 2 nghiệm

t = 1( thỏa mãn t ≥ 0); t = -5 ( không thỏa mãn t ≥ 0)

với t = 1 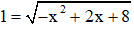(ĐK: -x² + 2x +8 ≥ 0)

Hai nghiệm tìm được thỏa mãn điều kiện

Vậy phương trình có hai nghiệm x = 1 ± √8

Dạng 4:

+ Đặt 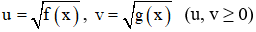(u, v ≥ 0)

+ Đưa phương trình đã cho về hệ phương trình với hai ẩn là u, v

+ Giải hệ tìm u, v sau đó tìm x

Ví dụ: Giải phương trình 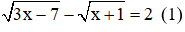(1)

Giải

Với việc đặt ẩn phụ như trên thì phương trình (1): u – v = 2(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Ta có v = 0 và v = 2 đều thỏa mãn điều kiện v ≥ 0

Vậy phương trình có 2 nghiệm x =-1, x = 3

Dạng 5:

+ Đưa phương trình đã cho về hệ phương trình với ẩn là t

+ Giải phương trình tìm t, sau đó tìm x

Ví dụ: Giải phương trình

Giải

Với t = -2 (không thỏa mãn) ⇒ loại

Với t = 3 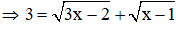(điều kiện x ≥ 1)

Ta thấy x = 2 thỏa mãn điều kiện x ≥1

Vậy phương trình có 1 nghiệm x = 2

B. Bài tập

Câu 1: Số nghiệm của phương trình 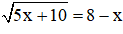là

A. 0

B. 1

C. 2

D. 3

Giải

Vậy phương trình có một nghiệm

Đáp án là B

Câu 2: Số nghiệm của phương trình 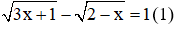là

A. 1

B. 2

C. 3

D. 4

Giải

Với việc đặt ẩn phụ như trên thì phương trình (1): u – v = 1(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Ta có v = 1 thỏa mãn điều kiện v ≥ 0 nên nhận

Ta có 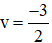không thỏa mãn điều kiện v ≥ 0 nên loại

Với 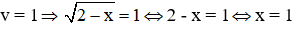(thỏa mãn)

Vậy phương trình có 1 nghiệm

Đáp án là A

Câu 3: Cho phương trình 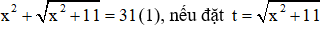thì phương trình (1) trở thành phương trình nào sau đây

Giải

Đặt . Khi đó phương trình đã cho trở thành: t² + t - 42 = 0

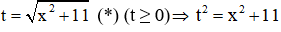
Đáp án đúng là D

Câu 4: Tổng các nghiệm của phương trình 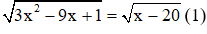(1) là

A. -3

B. 2

C. 10

D. không tồn tại

Giải

Vậy phương trình vô nghiệm

Đáp án là D

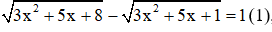
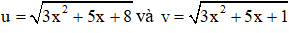
Câu 5: Cho phương trình (1), nếu đặt thì phương trình (1) trở thành hệ phương trình nào sau đây

Giải

Đặt (u, v ≥ 0)thì phương trình (1) trở thành: u – v = 1(*)

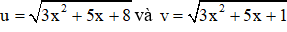
Đáp án đúng là B

Câu 6: Tích các nghiệm của phương trình 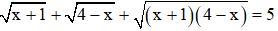(1) là

A. 0

B. 2

C. 1

D. không tồn tại

Giải

Với t = -5 (không thỏa mãn)⇒ loại

Với t = 3 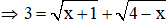(điều kiện -1≤ x ≤ 4)

Vậy phương trình có 2 nghiệm x = 0, x = 3

Suy ra tích các nghiệm bằng 0

Đáp án là A

Câu 7: Số nghiệm của phương trình 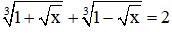(1) là

A. 1

B. 2

C. 3

D. 4

Giải

Điều kiện: x ≥ 0

Với việc đặt ẩn phụ như trên thì phương trình (1): u + v = 2(**)

Kết hợp (*) và (**) ta có hệ phương trình:

Theo vi-et ta có u, v là nghiệm của phương trình: x² – 2x + 1 = 0

Vậy phương trình có 1 nghiệm

Đáp án là A