Các dạng bài tập Toán 9 Chương 2 phần Hình học cực hay có đáp án | Toán lớp 9

Các dạng bài tập Toán 9 Chương 2 phần Hình học cực hay có đáp án

Với Các dạng bài tập Toán 9 Chương 2 phần Hình học cực hay có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Chương 2 phần Hình học từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Các dạng bài tập Toán 9 Chương 2 phần Hình học cực hay có đáp án

Các dạng bài tập về Đường tròn

II. Lý thuyết & Trắc nghiệm theo bài học

Lý thuyết, cách giải bài tập về Đường tròn

I. Lý thuyết chung về Đường tròn

1. Đường tròn tâm O, bán kính R, kí hiệu (O, R) là hình gồm các điểm cách điểm O cho trước một khoảng bằng R

2. Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn

3. Đường tròn là hình có tâm đối xứng và trục đối xứng

- Tâm đối xứng là tâm của đường tròn

- Trục đối xứng là bất kì đường kính nào

4. Trong các dây của đường tròn, đường kính là dây lớn nhất.

5. Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy. Đảo lại, trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

6. Trong một đường tròn:

- Hai dây bằng nhau thì cách đều tâm

- Hai dây cách đều tâm thì bằng nhau

7. Trong hai dây của một đường tròn:

- Dây nào lớn hơn thì gần tâm hơn

- Dây nào gần tâm hơn thì dây đó lớn hơn.

II. Ví dụ minh họa

Ví dụ 1: Cho tam giác ABC cân tại A. Gọi E là trung điểm của BC và BD là đường cao của ΔABC (D ∈ AC). Gọi giao điểm của AE và BD là H.

a) Chứng minh rằng bốn điểm A, D, E, B cùng thuộc một đường tròn tâm O

b) Xác định tâm I của đường tròn đi qua 3 điểm H; D; C

c) Chứng minh rằng đường tròn tâm O và đường tròn tâm I có hai điểm chung

Hướng dẫn:

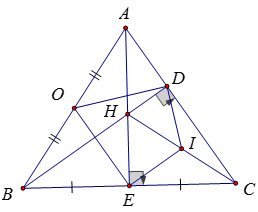
Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

a) Do tam giác ABC cân tại A nên AE ⊥ BC

Gọi O là trung điểm của đoạn thẳng AB. Theo tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông ta có:

Trong ΔDAB vuông tại D có DO là trung tuyến

⇒ OA = OB = OD

Trong ΔDAB vuông tại D có DO là trung tuyến

⇒ OA = OB = OD

Trong ΔABE vuông tại E có EO là trung tuyến

⇒ OA = OB = OE

⇒ OA = OB = OE = OD

⇒ Vậy A, B, E, D cũng thuộc đường tròn (O)

b) Gọi I là trung điểm của HC

Trong ΔHDC vuông tại D có DI là trung tuyến

⇒ ID = IH = IC

⇒ I là tâm đường tròn đi qua 3 điểm H, D, C

c) Trong ΔHEC vuông tại E có EI là trung tuyến

⇒ IE = IH = IC

⇒ E thuộc đường tròn (I)

Vậy (O) và (I) có hai điểm chung là E và D.

Ví dụ 2: Cho tam giác ABC, cạnh BC cố định, đường trung tuyến BM = 1,5 cm. Hỏi:

a) Trọng tâm G của tam giác di động trên đường nào?

b) Đỉnh A di động trên đường nào?

Hướng dẫn:

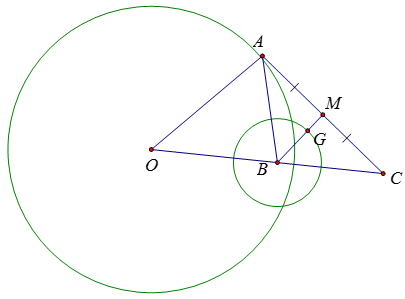
a) Vì G là trọng tâm của tam giác ABC nên

BG = 2/3; BM = 2/3.1,5 = 1 (cm)

Điểm G cách điểm B cho trước một khoảng là 1 cm nên G nằm trên đường tròn

(B; 1cm)

b) Trên tia đối của tia BC lấy điểm O sao cho BC = OB. Do BC cố định là O là cố định.

Ta có BM là đường trung bình của tam giác OAC nên OA = 2; BM = 3 cm

Do đó, điểm A nằm trên đường tròn (O; 3cm)

Nhận xét: Sẽ rất sai lầm nếu nói A nằm trên đường tròn tâm B, bán kính BA. Sai lầm ở chỗ đọ dài BA luôn thay đổi.

Ví dụ 3: Cho điểm M nằm trong đường tròn tâm O, M không trùng với O. Chứng minh rằng trong tất cả các dây đi qua M thì dây vuông góc với OM là dây ngắn nhất.

Hướng dẫn:

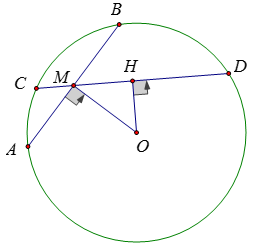
Gọi dây AB là dây đi qua M và OM vuông góc với AB; dây CD là dây đi qua M nhưng không vuông góc với OM. Ta phải chứng minh AB < CD

Vẽ OH ⊥ CD. Ta có: OH < OM (quan hệ giữa đường vuông góc và đường xiên)

⇒ CD > AB ( dây nào gần tâm hơn thì lớn hơn)

Vậy AB < CD

Vị trí tương đối của đường thẳng và đường tròn

Lý thuyết và Phương pháp giải

1. Bảng tóm tắt

Vị trí tương đối của đường thẳng và đường tròn

Số điểm chung

Hệ thức giữa d và R

Đường thẳng và đường tròn cắt nhau

Đường thẳng và đường tròn tiếp xúc nhau

Đường thẳng và đường tròn không giao nhau

d < R

d = R

d > R

Trong đó, d là khoảng cách từ tâm đường tròn đến đường thẳng.

2. Dấu hiệu nhận biết tiếp tuyến

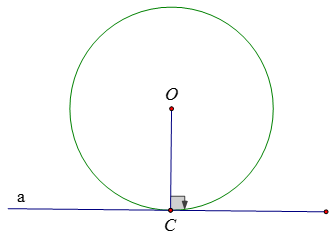
Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

3. Tính chất của tiếp tuyến

Nếu một đường thẳng là một tiếp tuyến của đường tròn thì nó vuông góc với bán kính đi qua tiếp điểm.

4. Tính chất của hai tiếp tuyến cắt nhau.

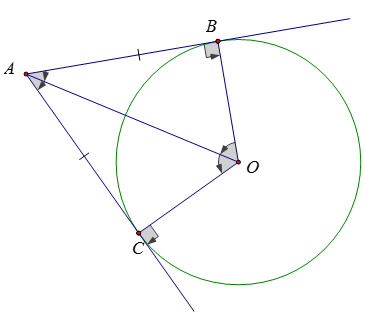
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:

- Điểm đó cách đều hai tiếp điểm.

- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.

- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.

5. Đường tròn nội tiếp tam giác

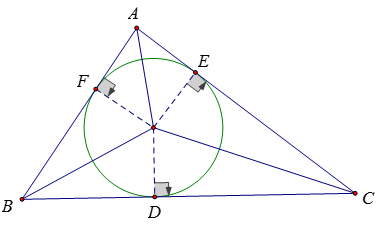
- Đường tròn tiếp xúc với ba cạnh của một tam giác gọi là đường tròn nội tiếp tam giác, còn tam giác gọi là ngoại tiếp đường tròn.

- Tâm đường tròn nội tiếp tam giác là giao điểm các đường phân giác các góc trong của tam giác.

6. Đường tròn bàng tiếp tam giác

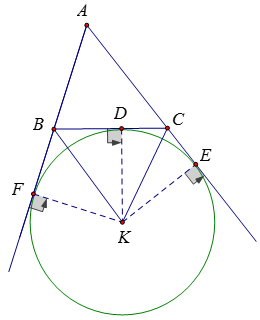
- Đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia gọi là đường tròn bàng tiếp tam giác.

- Tâm đường tròn bàng tiếp góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C.

Ví dụ minh họa

Ví dụ 1: Cho đoạn thẳng AB và hai tia Ax, By vuông góc với AB ở trên cùng nửa mặt phẳng bờ AB. Gọi O là trung điểm của AB. Xét góc vuông mOn quay quanh O sao cho Om cắt Ax tại C, On cắt By tại D. Chứng minh rằng:

a) CD luôn tiếp xúc với nửa đường tròn (O; AB/2)

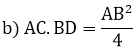
Hướng dẫn:

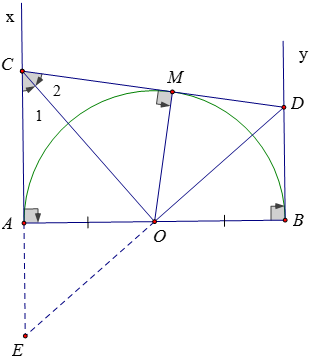
a) Kéo dài DO cắt tia đối của tia Ax tại E. Dễ thấy

ΔBOD = ΔAOE (g.c.g)

⇒ OD = OE

Mà CO ⊥ DE (gt)

⇒ ΔCDE cân tại C

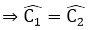
Kẻ OM ⊥ CD ta lại có:

ΔAOC = ΔMOC (cạnh huyền-góc nhọn)

⇒ OA = OM

Điều này chứng tỏ M thuộc đường tròn (O) nên CD là tiếp tuyến của đường tròn (O) hay CD tiếp xúc với nửa đường tròn (O; AB/2)

b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có:

AC = CM; DB = DM

⇒ AC. DB = CM. DM

Xét tam giác COD vuông tại O có OM là đường cao nên:

CM.DM = OM² = AB²/4

Vậy AC.DB = AB²/4

Ví dụ 2: Cho nửa đường tròn (O) đường kính AB. Lấy AO làm đường kính vẽ nửa đường tròn tâm O’ cùng phía với (O). Một cát tuyến bất kì qua A cắt (O’) và (O) lần lượt tại C và D.

a) Chứng minh C là trung điểm của AD và các tiếp tuyến tại C và D với các nửa đường tròn song song với nhau.

b) Hãy xác định điểm C sao cho BC là tiếp tuyến của (O’)

Hướng dẫn:

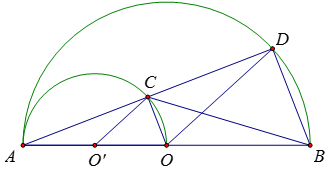
a) Vì C, D thuộc nửa đường tròn đường kính AO, AB nên

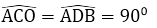
⇒ CO // BD

Mà OA = OB nên OC là đường trung bình của ΔABD

⇒ C là trung điểm của AD

Xét ΔAOD có O’C là đường trung bình

⇒ O’C // OD

⇒ Các tiếp tuyến tại C và D của (O’) và (O) phải song song với nhau ( vì cùng vuông góc với hai đường thẳng song song)

b) Nếu BC là tiếp tuyến của (O’) thì BC ⊥ CO' hay góc O'CB bằng 90⁰

⇒ C thuộc nửa đường tròn đường kính O’B

Vậy C là giao điểm của nửa đường tròn (O’) và nửa đường tròn đường kính O’B

Ví dụ 3: Cho tam giác ABC vuông tại A. Gọi (O₁; R₁ ) là đường tròn nội tiếp ΔABC và (O₂; R₂ ) là đường tròn ngoại tiếp tam giác ABC. Chứng minh:

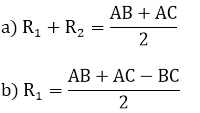
Hướng dẫn:

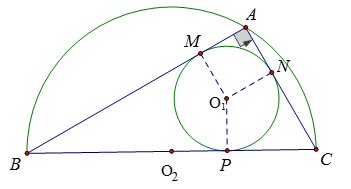
a) Gọi tiếp điểm của (O₁; R₁ ) với các cạnh AB, BC, CA lần lượt là M, P, N

Dễ thấy tứ giác AMO₁N là hình vuông

⇒ AM = AN = R₁

BM và BP là 2 tiếp tuyến của đường tròn (O₁; R₁ ) nên theo tính chất 2 tiếp tuyến cắt nhau, ta có BM = BP

Tương tự, CN và CP là 2 tiếp tuyến của đường tròn (O₁; R₁ ) nên CN = CP

Ta có:

AB + AC = AM + BM + AN + NC

AB + AC = 2R₁ + BP + CP

AB + AC = 2R₁ + BC = 2R₁+ 2R_2

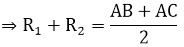
b) Theo câu a, ta có:

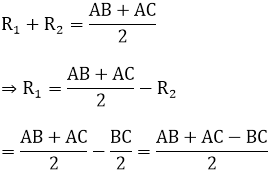
Ví dụ 4: Cho nửa đường tròn (O) đường kính AB; AC là một dây cung của nó. Kẻ tiếp tuyến Ax và kẻ đường phân giác của góc Cax cắt đường tròn tại E và cắt BC kéo dài tại D.

a) Chứng minh rằng ΔABD cân và OE // BD

b) Gọi I là giao điểm của AC và BE. Chứng minh DI ⊥ AB

c) Khi C di chuyển trên đường tròn (O) thì D chạy trên đường nào?

Hướng dẫn:

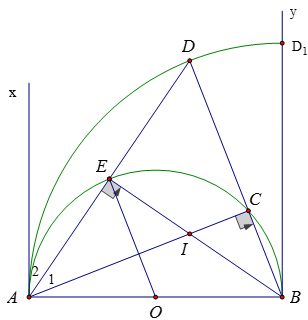
a) Vì C ∈ (O) nên Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Ta có: Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

Mà Chuyên đề Toán lớp 9 | Chuyên đề Lý thuyết và Bài tập Đại số và Hình học 9 có đáp án

⇒ ΔADB cân tại B.

Chứng minh OE // DB

Vì E ∈ (O) nên góc AEB bằng 90⁰ hay BE ⊥ AD

Do ΔADB cân tại B nên BE vừa là đường cao vừa là đường trung tuyến

⇒ E là trung điểm của AD

Lại có O là trung điểm của AB

Nên OE là đường trung bình của ΔADB

⇒ OE // BD

b) Ta có:

BE ⊥ AD

AC ⊥ BD

AC cắt BE tại I

⇒ I là trực tâm của ΔADB ⇒ DI ⊥ AB

c) Do ΔADB cân tại B nên BD = BA = 2R ⇒ D nằm trên đường tròn tâm B bán kính 2R

Giới hạn: Khi C di chuyển tới B thì D di chuyển tới D₁ (BD₁ = 2R), D₁ ∈ By,By ⊥ AB. Vậy D di chuyển trên cung một phần tư đường tròn ADD₁

Ví dụ 5: Chứng minh rằng diện tích của một tam giác bằng nửa chu vi của nó nhân với bán kính đường tròn nội tiếp .

Hướng dẫn:

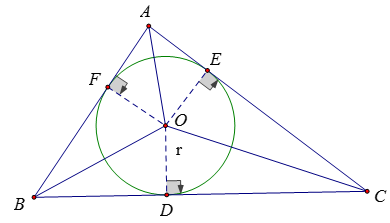
Ta có: OD ⊥ BC; OE ⊥ AC; OF ⊥ AB

Gọi S là diện tích của tam giác ABC.

S= S_AOB + S_BOC + S_COA

= 1/2.OF.AB + 1/2.OD.BC + 1/2.OE.AC

= 1/2.r.(AB + BC + CA)

= pr

Với p là nửa chu vi của tam giác, r là bán kính đường tròn nội tiếp tam giác.

Xem thêm các dạng bài tập Toán lớp 9 chọn lọc, có đáp án hay khác:

❮ Bài trước Bài sau ❯

Các dạng bài tập Toán lớp 9

Các dạng bài tập Toán 9 Chương 2 phần Hình học cực hay có đáp án | Toán lớp 9