Lý thuyết Giải bài toán bằng cách lập hệ phương trình hay, chi tiết | Toán lớp 9

Lý thuyết Giải bài toán bằng cách lập hệ phương trình hay, chi tiết

Tài liệu Lý thuyết Giải bài toán bằng cách lập hệ phương trình hay, chi tiết Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Giải bài toán bằng cách lập hệ phương trình từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

I. CÁC BƯỚC GIẢI TOÁN

Các bước giải bài toán bằng cách lập hệ phương trình:

    + Bước 1: Lập hệ phương trình:

    * Chọn hai ẩn và đặt điều kiện thích hợp cho chúng.

    * Biểu diễn các đại lượng chưa biết theo các ẩn và các đại lượng đã biết.

    * Lập hai phương trình biểu thị mối quan hệ giữa các đại lượng.

    + Bước 2: Giải hệ hai phương trình nói trên.

    + Bước 3: Trả lời: kiểm tra xem trong các nghiệm của hệ phương trình, nghiệm nào thích hợp với bài toán và kết luận .

II. MỘT SỐ KIẾN THỨC CẦN NHỚ

1. Các bài toán chuyển động

Kiến thức cần nhớ:

    + Quãng đường = Vận tốc . Thời gian.

    + Vận tốc tỷ lệ nghịch với thời gian và tỷ lệ thuận với quãng đường đi được:

    + Nếu hai xe đi ngược chiều nhau khi gặp nhau lần đầu: Thời gian hai xe đi được là như nhau, Tổng quãng đường 2 xe đi được bằng đúng quãng đường cần đi của 2 xe.

    + Nếu hai phương tiện chuyển động cùng chiều từ hai địa điểm khác nhau là A và B, xe từ A chuyển động nhanh hơn xe từ B thì khi xe từ A đuổi kịp xe từ B ta luôn có hiệu quãng đường đi được của xe từ A với quãng đường đi được của xe từ B bằng quãng đường AB

    + Đối với (Ca nô, tàu xuồng) chuyển động trên dòng nước: Ta cần chú ý:

Khi đi xuôi dòng: Vận tốc ca nô = Vận tốc riêng + Vận tốc dòng nước.

Khi đi ngược dòng: Vận tốc ca nô = Vận tốc riêng - Vận tốc dòng nước.

Vận tốc của dòng nước là vận tốc của một vật trôi tự nhiên theo dòng nước (Vận tốc riêng của vật đó bằng 0)

2. Bài toán liên quan đến năng suất lao động, công việc.

Ta cần chú ý: Khi giải các bài toán liên quan đến năng suất thì liên hệ giữa ba đại lượng là: Khối lượng công việc = năng suất lao động × thời gian

III. VÍ DỤ CỤ THỂ

Câu 1: Một người đi xe đạp từ A đến B cách nhau 24km. Khi đi từ B trở về A người đó tăng vận tốc thêm 4km/h so với lúc đi, nên thời gian về ít hơn thời gian đi là 30 phút. Tính vận tốc của xe đạp khi đi từ A đến B.

Hướng dẫn:

Đổi 30 phút = 1/2 giờ.

Gọi vận tốc của xe đạp khi đi từ A đến B là x (km/h, x > 0 ). Thời gian xe đi từ A đến B là 24/x (giờ).

Đi từ B về A, người đó đi với vận tốc x + 4 (km/h). Thời gian xe đi từ B về A là 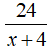(giờ)

Do thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:

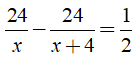
Giải phương trình:

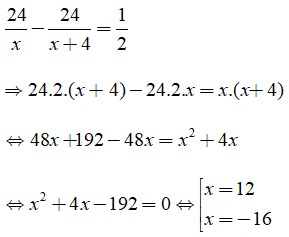
Đối chiếu với điều kiện ta có vận tốc của xe đạp đi từ A đến B là 12km/h.

Câu 2: Cho một bể cạn (không có nước). Nếu hai vòi nước cùng được mở để chảy vào bể này thì sẽ đầy bể sau 4 giờ 48 phút. Nếu mở riêng từng vòi chảy vào bể thì thời gian vòi một chảy đầy bể sẽ ít hơn thời gian vòi hai chảy đầy bể là 4 giờ. Hỏi mỗi vòi chảy một mình thì sau bao lâu sẽ đầy bể?

Hướng dẫn:

Đổi 4 giờ 48 phút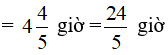

Cách 1: Lập hệ phương trình

Gọi thời gian vòi một chảy một mình đầy bể trong x (giờ, x > 24/5 )

Gọi thời gian vòi hai chảy một mình đầy bể trong y (giờ, y > 24/5 )

Biết hai vòi cùng chảy thì sau 24/5 giờ thì đầy bể nên ta có phương trình: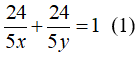

Nếu chảy riêng thì vòi một chảy đầy bể nhanh hơn vòi hai là 4 giờ nên ta có phương trình:

     x = y - 4     (2)

Từ (1) và (2) ta có hệ phương trình:

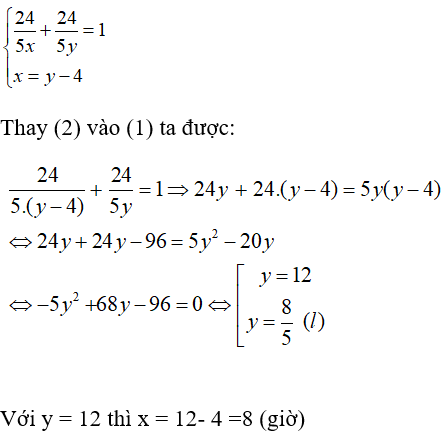
Vậy vòi một chảy một mình trong 8 giờ thì đầy bể và vòi hai chảy một mình trong 12 giờ thì đầy bể.

B. Bài tập tự luận

Câu 1: Đem một số có hai chữ số nhân với tổng của các chữ số với nhau thì được kết quả là 405. Nếu viết ngược lại bằng cách như vậy thì tích nhận được là 468. Tìm số đó?

Lời giải:

Mà a,b là các số tự nhiên nên b + a > b – a ; b + a> 0 và ( b+a); (b –a) đều là ước của 9.

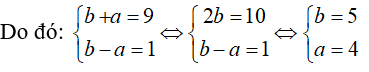
Vậy số cần tìm là 45.

Câu 2: Cho tam giác vuông, biết rằng nếu tăng mỗi cạnh góc vuông lên 2cm thì diện tích tăng 17 cm². Nếu giảm lần lượt các cạnh góc vuông, một cạnh 3cm, một cạnh 1cm thì diện tích giảm đi 11 cm² . Tính các cạnh của tam giác vuông ấy

Lời giải:

Gọi hai cạnh góc vuông là x, y (cm) (x > 3; y > 1)

Diện tích ban đầu của tam giác là:

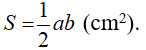
Theo đề bài: tăng mỗi cạnh góc vuông lên 2cm thì diện tích tăng thêm 17 cm² , ta có phương trình:

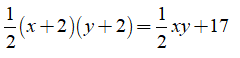
Giảm lần lượt các cạnh góc vuông, một cạnh giảm 3cm, một cạnh giảm 1cm thì diện tích giảm đi 11 cm² , ta có phương trình:

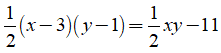
Khi đó ta có hệ phương trình:

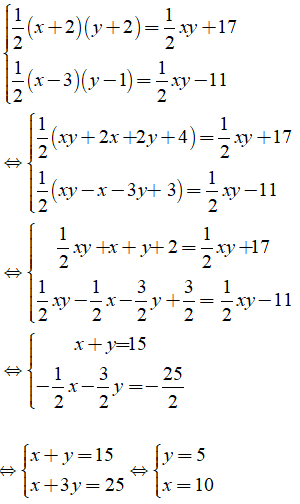
Vậy độ dài ba cạnh của tam giác là 5 cm; 10 cm; 5√5 cm