Lý thuyết Chương 1: Hệ thức lượng trong tam giác vuông đầy đủ nhất | Toán lớp 9

Lý thuyết Chương 1: Hệ thức lượng trong tam giác vuông đầy đủ nhất

Tài liệu Lý thuyết Chương 1: Hệ thức lượng trong tam giác vuông đầy đủ nhất Toán lớp 9 sẽ tóm tắt kiến thức trọng tâm về Chương 1: Hệ thức lượng trong tam giác vuông từ đó giúp học sinh ôn tập để nắm vứng kiến thức môn Toán lớp 9.

Chủ đề 1: Hệ thức về cạnh và đường cao trong tam giác vuông

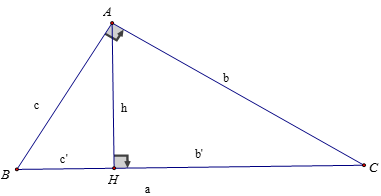
    Cho ΔABC, góc A bằng 90⁰, AH ⊥ BC, AB = c, AC = b, BC = a, AH = h thì:

        + BH = c' được gọi là hình chiếu của AB xuống BC

        + CH = b' được gọi là hình chiếu của AC xuống BC

    Khi đó, ta có:

    1) AB² = BH.BC hay c² = a.c'

    AC² = CH.BC hay b² = a.b'

    2) AH² = CH.BH hay h² = b'.c'

    3) AB.AC = AH.BC hay b.c = a.h

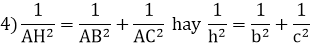
    5) AB² + AC² = BC² hay b² + c² = a² (Định lý Pytago)

Chủ đề 2: Tỉ số lượng giác của góc nhọn

1. Định nghĩa

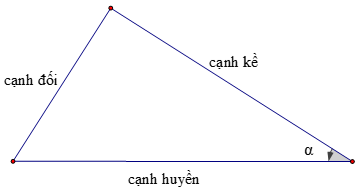
2. Định lí

    Nếu hai góc phụ nhau thì sin góc này bằng cosin góc kia, tang góc này bằng cotang góc kia.

3. Một số hệ thức cơ bản

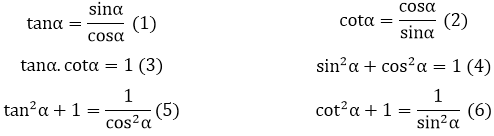
4. So sánh các tỉ số lượng giác

    a) Cho α,β là hai góc nhọn. Nếu α < β thì

    * sinα < sinβ; tanα < tanβ

    *cosα > cosβ; cotα > cotβ

    b) sinα < tanα; cosα < cotα

Chủ đề 3: Hệ thức về góc và cạnh trong tam giác vuông

1. Các hệ thức

    Trong một tam giác vuông, mỗi cạnh góc vuông bằng:

    a) Cạnh huyền nhân với sin góc đối hoặc nhân với cos góc kề

    b) Cạnh góc vuông kia nhân với tan góc đối hoặc cot góc kề

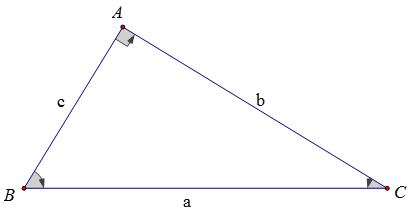
    b = a.sinB = a.cosC

    c = a.sinC = a.cosB

    b = c.tanB = c.cotC

    c = b.tanB = b.cotC

2. Giải tam giác vuông

    Là tìm tất cả các yếu tố còn lại của một tam giác vuông khi biết trước hai yếu tố (trong đó có ít nhất một yếu tố về cạnh và không kể góc vuông)