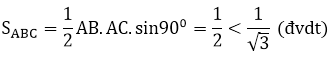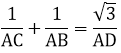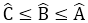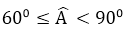Bài tập tính diện tích tam giác bằng tỉ số lượng giác chọn lọc, có lời giải | Toán lớp 9

Bài tập tính diện tích tam giác bằng tỉ số lượng giác chọn lọc, có lời giải

Với Bài tập tính diện tích tam giác bằng tỉ số lượng giác chọn lọc, có lời giải Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập tính diện tích tam giác bằng tỉ số lượng giác từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Bài 1: Chứng minh rằng nếu tất cả các cạnh của một tam giác nhỏ hơn 2 thì diện tích của tam giác nhỏ hơn √3 (đvdt)

Bài 2: Cho tam giác ABC, góc A bằng 60⁰, đường phân giác AD. Chứng minh rằng:

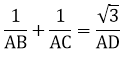
Bài 3: Cho tam giác ABC có: 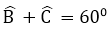, AB = 4 cm; AC = 6 cm. Tính độ dài đường phân giác AD.

Bài 4: Cho tam giác nhọn ABC. Chứng minh hệ thức:

    sinA = sinB.cosC + sinC.cosB

Bài 5: Cho tam giác nhọn ABC, điểm D thuộc cạnh BC sao cho AD = BC. Chứng minh rằng sinA ≥ sinB.sinC

Bài 6: Cho tam giác ABC cân tại A, AB = AC = 5 cm, góc A bằng 30⁰. Trên tia đối của các tia AB và AC lần lượt lấy các điểm M và N sao cho AM + AN = 6 cm. Tính diện tích lớn nhất của tứ giác BCMN

Bài 7: Cho tam giác ABC. Trên các cạnh BC, CA, AB lần lượt lấy các điểm D, E, F. Biết rằng các đoạn thẳng AD, BE, CF không lớn hơn 1. Chứng minh rằng

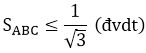
Đáp án và hướng dẫn giải

Bài 1:

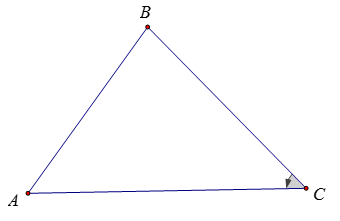
    Giả sử góc C ̂là góc nhỏ nhất của tam giác ABC

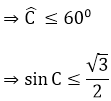
    Ta có:

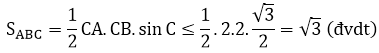
Bài 2:

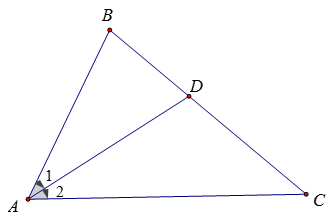
    Ta có: S_ABC = S_ABD + S_ADC

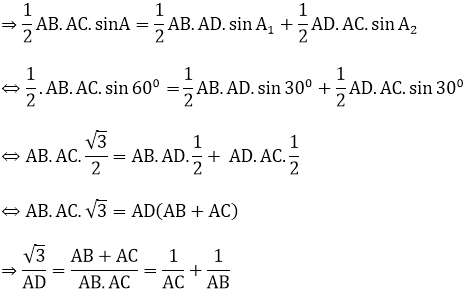
    Vậy

Bài 3:

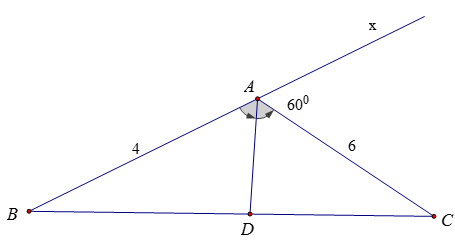
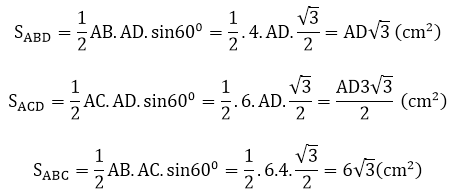
    Vì S_ABC = S_ABD + S_ACD nên:

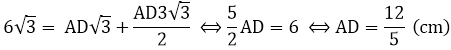
Bài 4:

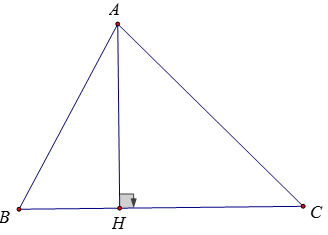
    Vẽ đường cao AH, H nằm giữa B và C

    Ta có:

    Vậy sin⁡B.cosC + sinC.cosB = sinA

Bài 5:

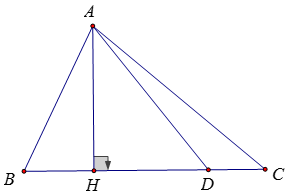
    Vẽ AH vuông góc với BC

    Gọi S là diện tích tam giác ABC

    Xét các tam giác ABH và ACH vuông tại H, ta có:

    AH = AB.sin⁡B = AC.sin⁡C

    ⇒ AH² = AB.AC.sin⁡B.sin⁡C

    Ta có: AD ≥ AH (dấu bằng xảy ra khi D ≡ H)

    Do đó: BC ≥ AH ⇔ BC.AH ≥ AH² = AB.AC.sin⁡B.sin⁡C (1)

    Mặt khác, ta có:

    BC.AH = 2S = 2.1/2 AB.AC.sinA (2)

    Từ (1) và (2) ⇒ AB.AC.sinA ≥ AB.AC.sin⁡B.sin⁡C

    Hay sinA ≥ sin⁡B.sin⁡C

    Dấu bằng xảy ra khi D trùng với H.

Bài 6:

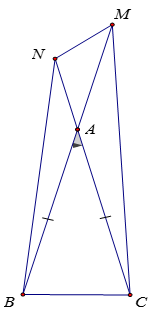
    Ta có: BM + CN = AB + AC + AM + AN = 5 + 5 + 6 = 16 (cm)

    Diện tích tứ giác BNMC là:

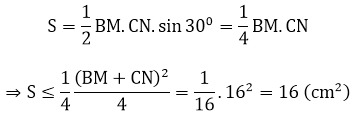
    Dấu bằng xảy ra khi BM = CN ⇔ AN = AM = 3 cm

Bài 7:

    Không mất tính tổng quát, giả sử

    Xét ba trường hợp:

    TH1: Tam giác ABC nhọn. Khi đó:

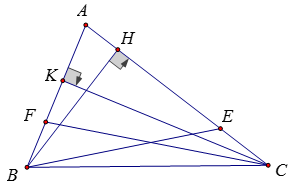
    Vẽ các đường cao BH, CK

    Ta có: BH ≤ BE ≤ 1; CK ≤ CF ≤ 1

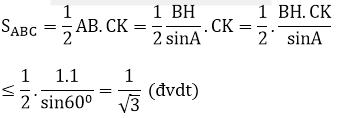
    TH2: Tam giác ABC tù, khi đó góc A lớn hơn 90⁰ và α = 180⁰ - α < 90⁰

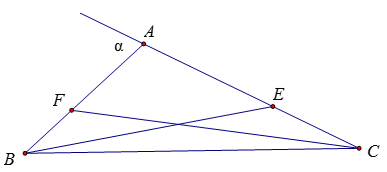
    Trong tam giác ABE, cạnh BE đối diện với góc tù nên là cạnh lớn nhất

    Do đó: AB < BE ≤ 1

    Tương tự: AC < CF ≤ 1

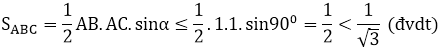
    TH3: Tam giác ABC vuông

    Khi đó góc A bằng 90⁰ và