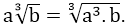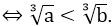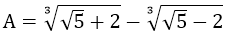Lý thuyết, các dạng bài tập Căn bậc ba cực hay, có đáp án | Toán lớp 9

Lý thuyết, các dạng bài tập Căn bậc ba cực hay, có đáp án

Với Lý thuyết, các dạng bài tập Căn bậc ba cực hay, có đáp án Toán lớp 9 tổng hợp các dạng bài tập, bài tập trắc nghiệm có lời giải chi tiết với đầy đủ phương pháp giải, ví dụ minh họa sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Căn bậc ba từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Lý thuyết và Phương pháp giải

    1. Định nghĩa: Căn bậc ba của một số a, kí hiệu là 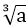là số x sao cho x³ = a.

    +) Cho a ∈ R; ³√a = x ⇔ x³ = (∛a)³ = a

    +) Mỗi số thực a đều có duy nhất một căn bậc ba

    +) Nếu a > 0 thì ³√a > 0

    +) Nếu a = 0 thì ³√a = 0

    +) Nếu a < 0 thì ³√a < 0

    2. Tính chất

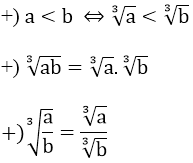
    3. Các phép biến đổi căn bậc ba

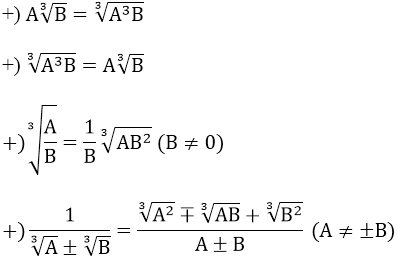
Ví dụ minh họa

Ví dụ 1: So sánh:

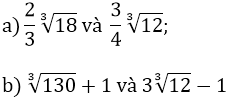
Hướng dẫn:

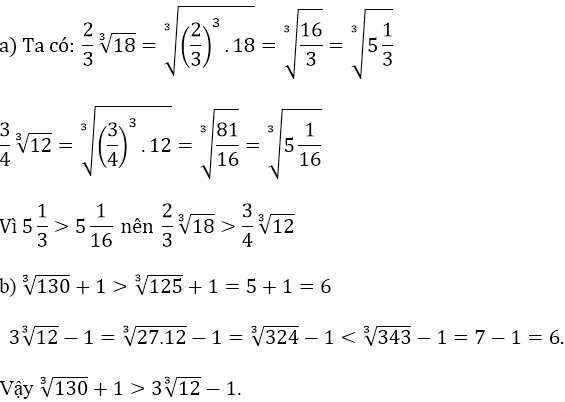
    Chú ý:

    + Đưa thừa số vào trong dấu căn:

    + So sánh hai số trong dấu căn: a < b

Ví dụ 2: Tính:

Hướng dẫn:

    Để tính giá trị của A, ta tính A³ sau đó suy ra A

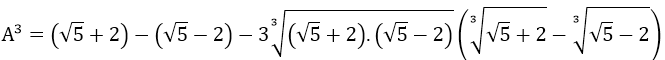
    ⇔ A³ = 4 - 3.A ⇔ A³ + 3A - 4 = 0

    ⇔ (A - 1)(A² + A + 4) = 0

    ⇔ A - 1 = 0 (vì A² + A + 4 > 0)

    ⇔ A = 1

    Vậy A = 1.

Ví dụ 3: Giải phương trình sau:

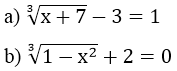
Hướng dẫn:

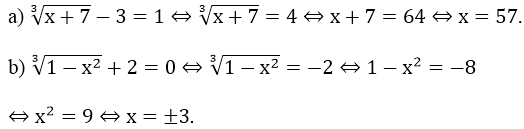
Ví dụ 4: Cho biểu thức:

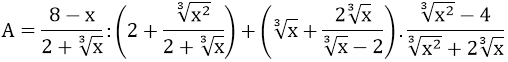
    Với x ≠ ±8, x ≠ 0

    Chứng minh rằng giá trị của A không phụ thuộc vào x.

Hướng dẫn:

    Đặt ³√x = y (y ≠ 0). Biểu thức A có dạng:

    = 2 - y + y

    = 2

    Vậy với x ≠ ±8, x ≠ 0 thì A = 2, không phụ thuộc vào giá trị của x.