Cách dựng cạnh huyền, dựng đoạn trunh bình nhân của hai đoạn thẳng cho trước | Toán lớp 9

Cách dựng cạnh huyền, dựng đoạn trunh bình nhân của hai đoạn thẳng cho trước

Với Cách dựng cạnh huyền, dựng đoạn trunh bình nhân của hai đoạn thẳng cho trước Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập dựng cạnh huyền, dựng đoạn trunh bình nhân của hai đoạn thẳng cho trước từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

1. Dựng đoạn thẳng Py – ta – go

• Loại 1: Cho trước hai đoạn thẳng a và b. Dựng đoạn thẳng

x = 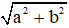⇔ x² = a² + b²

Dựng tam giác vuông có hai cạnh góc vuông là a và b thì cạnh huyền bằng x.

• Loại 2: Cho trước hai đoạn thẳng a và b. Dựng đoạn thẳng

y = 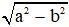, (a > b) ⇔ y² + b² = a²

Dựng tam giác vuông có cạnh huyền là a, cạnh góc vuông là b thì cạnh góc vuông còn lại là y.

2. Dựng đoạn trung bình nhân

• Cho trước hai đoạn thẳng a và b. Dựng đoạn thẳng x = .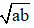

• Dựng tam giác ABC có cạnh huyền BC = a + b, (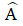 = 90⁰) thì đường cao AH ứng với cạnh huyền là x với BH = a, CH = b.

B. Ví dụ minh họa

Ví dụ 1: Dựng đoạn thẳng 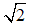bằng cách dựng đoạn Py – ta – go.

Bài giải:

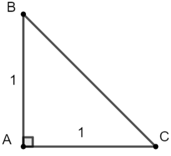
Dựng tam giác ABC vuông cân tại A có AB = AC = 1 (đvđd)

Áp dụng định lý Py – ta – go cho ΔABC ta có:

BC² = AB² + AC² ⇔ BC² = 1² + 1² = 2

⇒ BC = 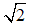(đvđd)

Vậy đoạn thẳng 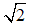cần dựng chính là cạnh huyền BC.

Ví dụ 2: Dựng đoạn thẳng 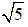bằng cách dựng đoạn Py – ta – go.

Bài giải:

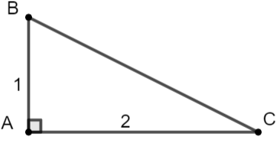
Dựng tam giác ABC vuông tại A có AB = 1(đvđd) và AC = 2 (đvđd)

Áp dụng định lý Py – ta – go cho ΔABC ta có:

BC² = AB² + AC² ⇔ BC² = 1² + 2² = 1 + 4 = 5

⇒ BC = 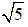(đvđd)

Vậy đoạn thẳng 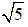cần dựng chính là cạnh huyền BC.

Ví dụ 3: Dựng đoạn thẳng 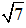bằng cách dựng đoạn Py – ta – go.

Bài giải:

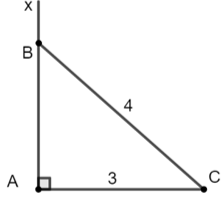
Dựng đoạn AC = 3 (đvđd)

Dựng góc = 90⁰

Dựng cung tròn tâm C bán kính 4 (đvđd) cắt Ax tại B.

Nối BC ta được tam giác ABC vuông tại A có: = 90⁰; AC = 3; BC = 4

Áp dụng định lý Py – ta – go cho ΔABC ta được:

AB² = BC² - AC² = 4² - 3² = 16 – 9 = 7 ⇒ AB = 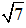(đvđd)

Vậy AB là đoạn ta cần dựng.

Ví dụ 4: Dựng đoạn thẳng 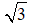bằng cách dựng đoạn trung bình nhân.

Bài giải:

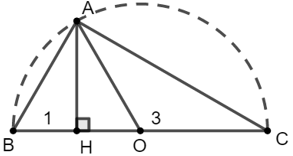
Dựng nửa đường tròn (O) đường kính BC = 4 (đvđd)

Trên BC lấy H sao cho BH = 1 (đvđd) và CH = 3 (đvđd)

Từ H dựng AH ⊥ BC tại H, A ∈ (O)

Xét ΔABC có: OA = OB = OC =

⇒ ΔABC vuông tại A (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)

Áp dụng hệ thức lượng trong ΔABC vuông tại A có đường cao AH ta được:

AH² = BH.CH ⇒ AH² = 1.3 = 3 ⇒ AH = 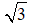(đvđd)

Vậy đoạn thẳng cần dựng là AH.

Ví dụ 5: Dựng đoạn thẳng 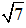bằng cách dựng đoạn trung bình nhân.

Bài giải:

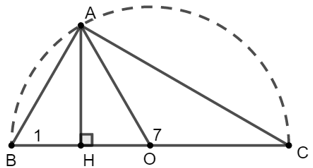
Dựng nửa đường tròn (O) đường kính BC = 8 (đvđd)

Trên BC lấy H sao cho BH = 1 (đvđd) và CH = 7 (đvđd)

Từ H dựng AH ⊥ BC tại H, A ∈ (O)

Xét ΔABC có: OA = OB = OC =

⇒ ΔABC vuông tại A (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)

Áp dụng hệ thức lượng trong ΔABC vuông tại A có đường cao AH ta được:

AH² = BH.CH ⇒ AH² = 1.7 = 7 ⇒ AH = 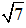(đvđd)

Vậy đoạn thẳng cần dựng là AH.

Ví dụ 6: Dựng đoạn thẳng 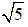bằng cách dựng đoạn trung bình nhân.

Bài giải:

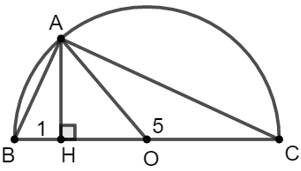
Dựng nửa đường tròn (O) đường kính BC = 6 (đvđd)

Trên BC lấy H sao cho BH = 1 (đvđd) và CH = 5 (đvđd)

Từ H dựng AH ⊥ BC tại H, A ∈ (O)

Xét ΔABC có: OA = OB = OC =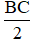

⇒ ΔABC vuông tại A (đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)

Áp dụng hệ thức lượng trong ΔABC vuông tại A có đường cao AH ta được:

AH² = BH.CH ⇒ AH² = 1.5 = 5 ⇒ AH = 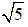(đvđd)

Vậy đoạn thẳng cần dựng là AH.