Bài tập Cung chứa góc chọn lọc, có đáp án | Toán lớp 9
Bài tập Cung chứa góc chọn lọc, có đáp án
Với Bài tập Cung chứa góc chọn lọc, có đáp án Toán lớp 9 tổng hợp bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Cung chứa góc từ đó đạt điểm cao trong bài thi môn Toán lớp 9.
Câu 1: Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là
A. Đường tròn đường kính AB
B. Nửa đường tròn đường kính AB
C. Đường tròn đường kính AB/2
D. Đường tròn bán kính AB
Lời giải:
Quỹ tích các điểm M nhìn đoạn thẳng AB cho trước dưới một góc vuông là đường tròn đường kính AB
Chọn đáp án A
Câu 2: Với đoạn thẳng AB và góc α(0° < α < 180°) cho trước thì quỹ tích các điểm M thỏa mãn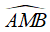 
= α là
A. Hai cung chứa góc α dựng trên đoạn AB . Hai cung này không đối xứng nhau qua
B. Hai cung chứa góc α dựng trên đoạn AB và không lấy đoạn AB
C. Hai cung chứa góc α dựng trên đoạn AB . Hai cung này đối xứng nhau qua
D. Một cung chứa góc α dựng trên đoạn AB
Lời giải:
Với đoạn thẳng AB và góc α(0° < α < 180°) cho trước thì quỹ tích các điểm thỏa mãn 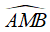= α là hai cung chứa góc α dựng trên đoạn AB
Hai cung chứa góc α nói trên là hai cung tròn đối xứng nhau qua AB . Hai điểm A, B được coi là thuộc quỹ tích
Chọn đáp án C
Câu 3: Cho tam giác ABC có BC cố định và góc A bằng 50° . Gọi D là giao điểm của ba đường phân giác trong tam giác. Tìm quỹ tích điểm D
A. Một cung chứa góc 115° dựng trên đoạn BC
B. Một cung chứa góc 115° dựng trên đoạn AC
C. Hai cung chứa góc 115° dựng trên đoạn AB
D. Hai cung chứa góc 115° dựng trên đoạn BC
Lời giải:
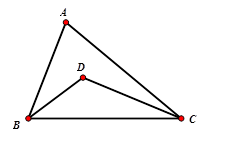
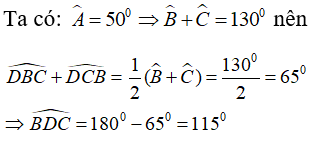
Quỹ tích của điểm D là hai cung chứa góc 115° dựng trên đoạn BC
Chọn đáp án D
Câu 4: Cho các hình thoi ABCD có cạnh AB cố định . Tìm quỹ tích giao điểm của hai đường chéo của hình thoi đó .
A. Quỹ tích điểm O là 2 cung chứa góc 120° dựng trên AB
B. Quỹ tích điểm O là nửa đường tròn đường kính AB, trừ hai điểm A và B
C. Quỹ tích điểm O là 2 cung chứa góc 60° dựng trên AB
D. Quỹ tích điểm O là 2 cung chứa góc 30° dựng trên AB
Lời giải:
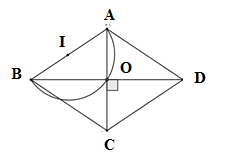
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau tại trung điểm của mỗi đường
Suy ra AO ⊥ BO ⇒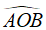 
= 90°
Ta có 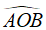= 90° không đổi mà cố định
⇒ Quỹ tích điểm O là nửa đường tròn đường kính AB trừ hai điểm A và B
Chọn đáp án B
Câu 5: Cho tứ giác ABCD có 2 đường chéo vuông góc với nhau tại O.Biết 2 điểm A và B cố định, 2 điểm C và D di chuyển. Tìm quỹ tích điểm O
A. Đường tròn đường kính AB.
B. Đường tròn bán kính AB.
C. Đường tròn bán kính AB/2
D. Đường tròn đường kính 2AB
Lời giải:
Ta có: AC vuông góc BD tại O nên: 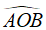= 90°
Suy ra: quỹ tích điểm O là đường tròn đường kính A
B.
Chọn đáp án A.
Câu 6: Cho đoạn thẳng BC cố định. Lấy điểm A bất kì sao cho tam giác ABC cân tại
A. Tìm quỹ tích điểm A?
A. Đường tròn tâm B bán kính BC.
B. Đường tròn tâm C bán kính BC.
C. Đường trung trực của đoạn thẳng BC.
D. Đường tròn đường kính BC.
Lời giải:
Do tam giác ABC cân tại A nên AB = AC
Suy ra, A thuộc đường trung trực của đoạn thẳng B
C.
Chọn đáp án C.
Câu 7: Cho hai điểm B và C cố định, lấy điểm A bất kì sao cho tam giác ABC vuông tại
A.
Gọi M và N lần lượt là trung điểm BC và A
C. Tìm quỹ tích điểm N .
A. Đường tròn đường kính MC
B. Đường tròn đường kính BC
C. Đường tròn đường kính BM.
D. Đáp án khác
Lời giải:
Xét tam giác ABC có M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB
C.
Suy ra: MN// AB
Lại có: AB ⊥ AC ⇒ MN ⊥ AC
Suy ra: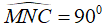 
Vì B và C cố định nên trung điểm M của BC cũng cố định
Do đó, quỹ tích các điểm N là đường tròn đường kính MC.
Chọn đáp án A.
Câu 8: Cho hai điểm B và C cố định. Lấy A là điểm bất kì sao cho tam giác ABC cân tại
A. Gọi H là trực tâm của tam giác AB
C. Tìm quỹ tích điểm H
A. Đường tròn đường kính BC
B. Đường trung trực của đoạn thẳng BC
C. Đường tròn tâm B, bán kính BC
D. Đường tròn tâm C, bán kính BC
Lời giải:
Vì H là trực tâm của tam giác ABC nên AH ⊥ BC
Lại có tam giác ABC là tam giác cân tại A nên đường cao AH đồng thời là đường trung trực.
Suy ra: H nằm trên đường trung trực của đoạn thẳng BC.
Chọn đáp án B.
