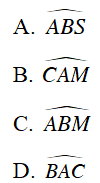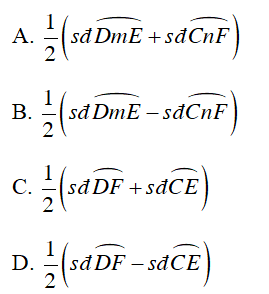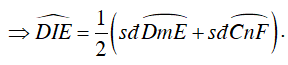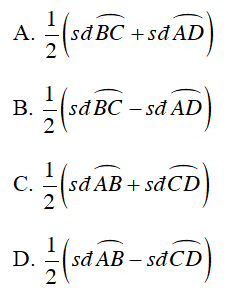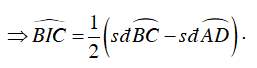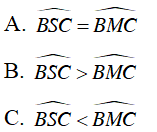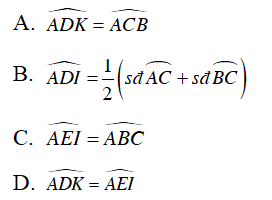Cách chứng minh hai góc hoặc hai đoạn thẳng bằng nhau cực hay, chi tiết | Toán lớp 9

---

Cách chứng minh hai góc hoặc hai đoạn thẳng bằng nhau cực hay, chi tiết

Với Cách chứng minh hai góc hoặc hai đoạn thẳng bằng nhau cực hay, chi tiết Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập chứng minh hai góc hoặc hai đoạn thẳng bằng nhau từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Tải xuống

A. Phương pháp giải

+ Ta thường sử dụng các kiến thức về số đo của góc có đỉnh bên trong và bên ngoài đường tròn, góc nội tiếp, góc tạo bởi tiếp tuyến và dây cung để chứng minh các góc bằng nhau

+ Sử dụng định lý Pytago, hệ thức lượng trong tam giác vuông để tính toán.

+ Sử dụng công thức tính góc có đỉnh bên trong đường tròn:

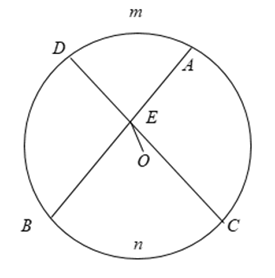
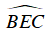
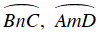
- Góc là góc có đỉnh nằm ở bên trong đường tròn chắn hai cung là .

- Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

Hay .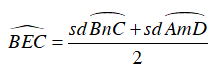

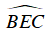
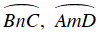
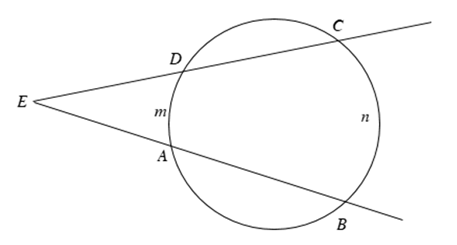
- Góc là góc có đỉnh nằm ở bên ngoài đường tròn chắn hai cung là .

- Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

Hay .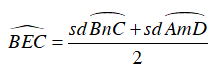

B. Ví dụ minh họa

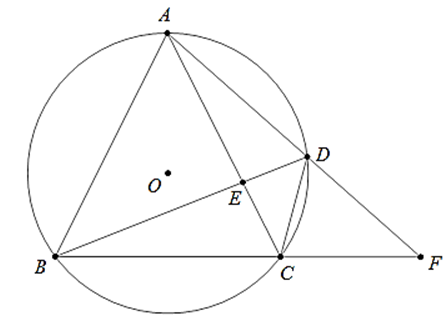
Ví dụ 1 : Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Điểm D di chuyển trên cung AC, E là giao điểm của AC với BD, F là giao điểm của AD và BC. Chứng minh rằng: .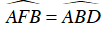

Hướng dẫn giải

Do tam giác ABC cân tại A

Nên AB = AC suy ra: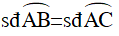

Ta có: 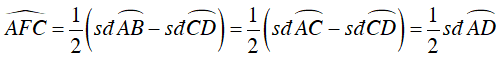(góc có đỉnh nằm bên ngoài đường tròn).

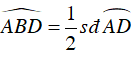
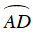
Mặt khác: (góc nội tiếp chắn cung ).

Do đó, .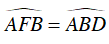

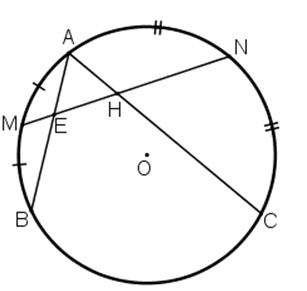
Ví dụ 2 : Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.

Hướng dẫn giải

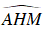
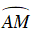
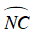
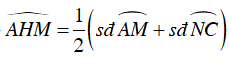
+ Do góc là góc có đỉnh bên trong đường tròn chắn hai cung và .

⇒ (1)

+ Do góc là góc có đỉnh bên trong đường tròn chắn hai cung và .

⇒ (2)

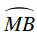
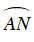
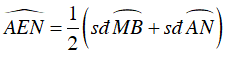
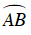
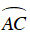
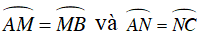
+ Do M và N là điểm chính giữa cung và

⇒

Suy ra 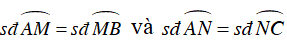(3)

Từ (1), (2) và (3) suy ra: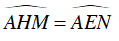

Do đó, tam giác AEH là tam giác cân tại A.

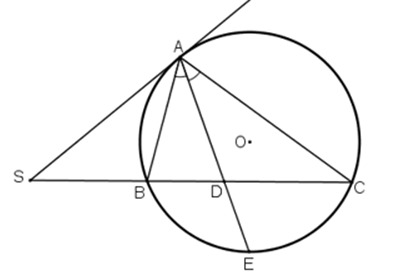
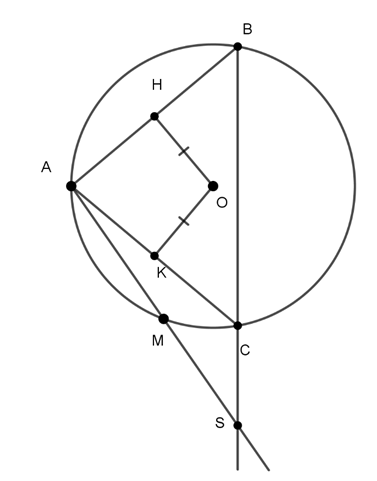
Ví dụ 3 : Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn . Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.

Hướng dẫn giải

Tia phân giác AD cắt (O) tại E.

+ là góc có đỉnh nằm bên trong đường tròn

⇒ (1)

+ là góc tạo bởi tiếp tuyến AS và dây AE

⇒ (2)

+ lần lượt là các góc nội tiếp chắn các cung và

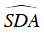
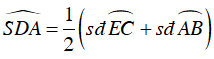
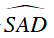
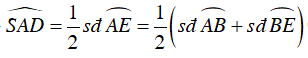
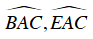
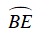
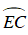
Mà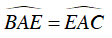

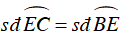
⇒ (3)

Từ (1); (2) và (3) suy ra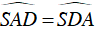

⇒ ΔSAD cân tại S

⇒ SA = SD.

C. Bài tập trắc nghiệm

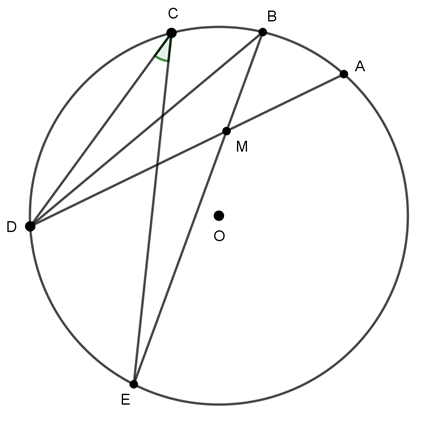
Câu 1 : Dựa vào hình vẽ sau, biết B là điểm chính giữa cung nhỏ AC. M là giao điểm của AD và BE, . Lúc đó góc

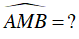
A. 30^o

B. 45^o

C. 60^o

D. 90^o

Hướng dẫn giải

Đáp án B

Ta có B là điểm chính giữa cung AC

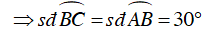
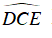
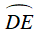
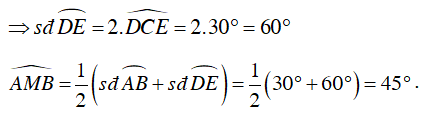
Ta có là góc nội tiếp chắn

Câu 2 : Cho đường tròn (O) và dây AB; AC cách đều tâm. Trên cung nhỏ AC lấy điểm M. Gọi S là giao điểm của AM và BC. Góc nào bằng góc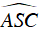

Hướng dẫn giải

Đáp án C

Ta có dây AB; AC cách đều tâm

(liên hệ giữa khoảng cách từ tâm đến dây)

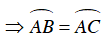
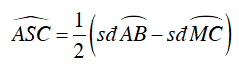
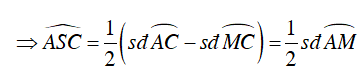
Ta có: (góc có đỉnh nằm ngoài đường tròn)

(1)

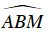
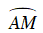
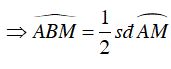
Mà là góc nội tiếp chắn

(2)

Từ (1) và (2) suy ra, .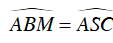

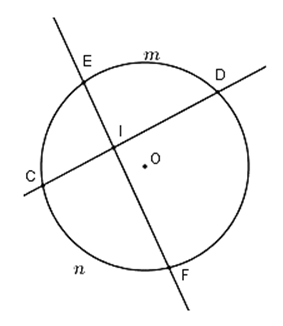
Câu 3 : Cho hình vẽ dưới đây , góc DIE có số đo bằng

Hướng dẫn giải

Đáp án A

Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn

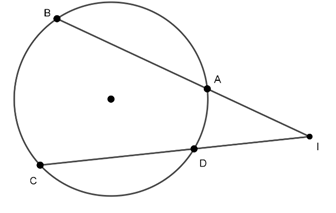
Câu 4 : Cho hình vẽ dưới đây , góc BIC có số đo bằng

Hướng dẫn giải

Đáp án B

Số đo của góc có đỉnh nằm bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

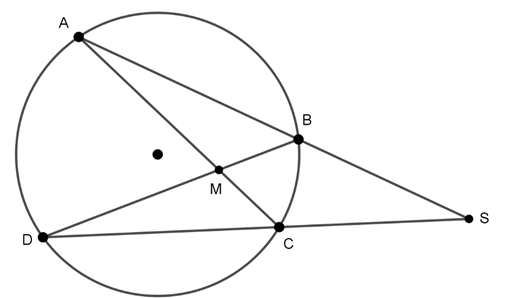
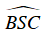
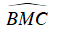
Câu 5 : Cho đường tròn (O) và 4 điểm A,B, C, D cùng nằm trên đường tròn sao cho AC và BD cắt nhau tại điểm M nằm trong đường tròn, AB và CD cắt nhau tại điểm S nằm ngoài đường tròn. So sánh hai góc và

D. Không so sánh được

Hướng dẫn giải

Đáp án C

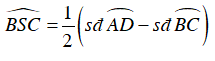
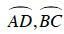
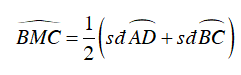
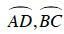
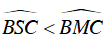
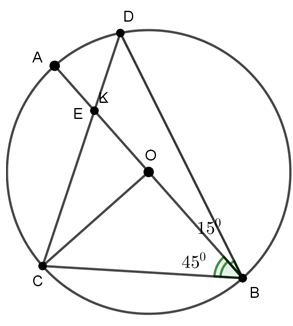
Ta có: (góc có đỉnh nằm ngoài đường tròn chắn hai cung )

(góc có đỉnh nằm ngoài đường tròn chắn hai cung )

⇒ .

Câu 6 : Số đo góc AED bằng bao nhiêu. Biết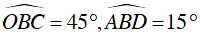

A. 30^o

B. 60^o

C. 90^o

D. 120^o

Hướng dẫn giải

Đáp án C

Tam giác OBC có OB = OC nên tam giác OBC cân tại O

(hai góc ở đáy)

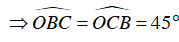
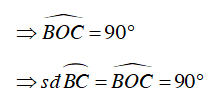
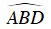
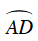
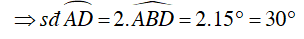
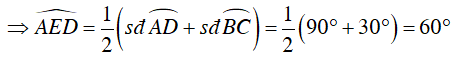
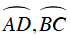
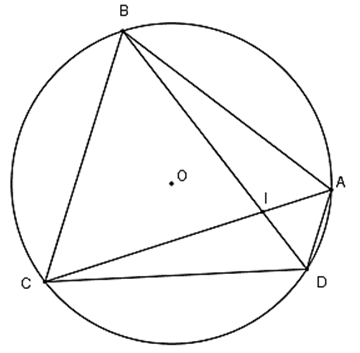
Ta lại có là góc nội tiếp chắn

(góc có đỉnh nằm trong đường tròn chắn hai cung ).

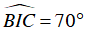
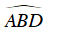
Câu 7 : Trên (O) lấy bốn điểm A, B, C, D theo thứ tự sao cho cung AB = cung BC = cung CD. Gọi I là giao điểm của BD và AC , biết . Tính

A. 20^o

B. 15^o

C. 35^o

D. 30^o

Hướng dẫn giải

Đáp án B

Vì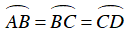

Gọi số đo mỗi cung là x độ.

Suy ra số đo cung AD là .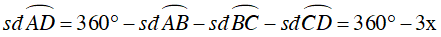

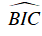
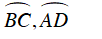
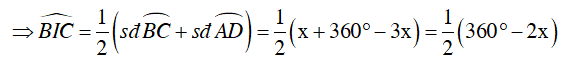
Vì là góc có đỉnh bên trong đường tròn chắn

Mà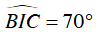

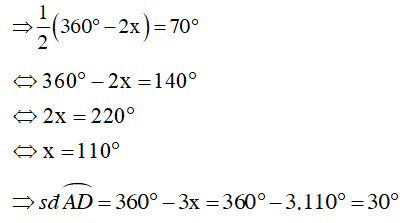
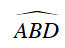
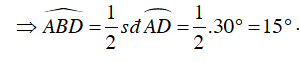
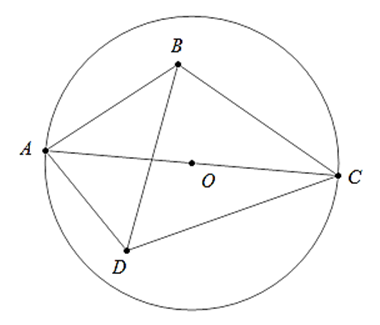
là góc nội tiếp chắn cung AD

.

Câu 8 : Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I và K sao cho 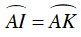. Dây IK cắt các cạnh AB, AC lần lượt tại D và E.

Khẳng định nào dưới đây là sai?

Hướng dẫn giải

Đáp án D

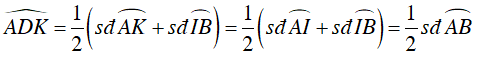
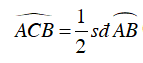
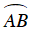
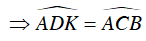
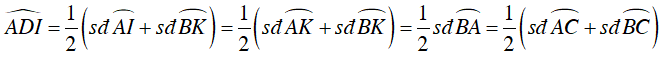
+ Ta có: (góc có đỉnh nằm trong đường tròn)

(góc nội tiếp chắn )

. Suy ra A đúng

+

(góc có đỉnh nằm bên trong đường tròn). Suy ra B đúng

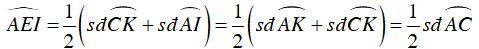
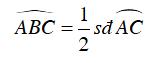
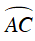
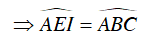
+ Ta có: (góc có đỉnh nằm trong đường tròn)

(góc nội tiếp chắn )

. Suy ra C đúng

Vậy D sai.

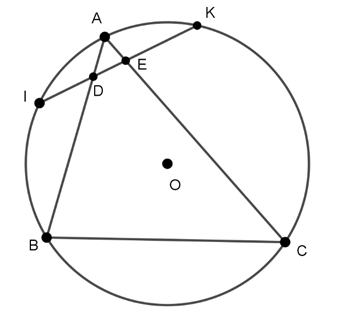
Câu 9 : Tứ giác ABCD có các góc B và D tù. Khẳng định nào sau đây đúng:

A. AC > BD

B. AC = BD

C. AC < BD

D. AC + BD = 2R

Hướng dẫn giải

Đáp án A

Vẽ đường tròn tâm O đường kính AC

Do 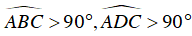nên B, D đều nằm bên trong đường tròn

Suy ra BD nhỏ hơn dây cung chứa nó

Mà AC là đường kính là dây cung lớn nhất trong đường tròn nên BD < AC.

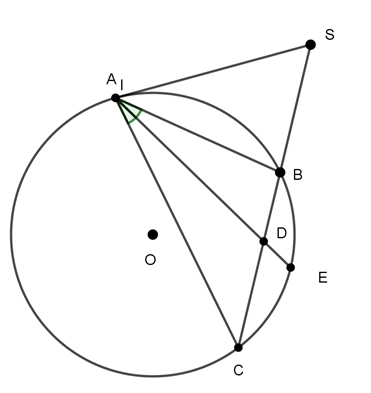
Câu 10 : Qua điểm S nằm ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC với đường tròn. Tia phân giác của góc BAC cắt dây BC tại D. Số phát biểu đúng trong các phát biểu sau:

I.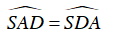

II. cân tại S

III. SA = SD

A. 0

B. 1

C. 2

D. 3

Hướng dẫn giải

Đáp án D

Gọi E là giao điểm của AD với đường tròn tâm O

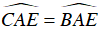
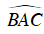
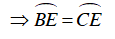
Vì (AD là phân giác của )

Ta có 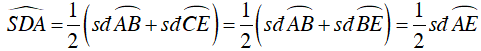(góc có đỉnh nằm bên trong đường tròn)

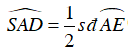
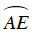
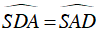
Ta lại có (góc tạo bởi tia tiếp tuyến và dây cung chắn )

⇒

⇒ ΔSAD cân tại S

⇒ SA = SD

Vậy cả ba phát biểu đều đúng.